Funkcja wykładnicza

Jak wskazuje sama nazwa, w funkcji wykładniczej nasza zmienna znajduje się w wykładniku potęgi, zatem:

Funkcja wykładnicza to funkcja postaci: $$f(x)=a^{x}$$ gdzie „a” jest stałą taką, że $a>0.$ (Czasem od a wymaga się również, aby było liczbą różną od 0, gdyż w tym przypadku funkcja upraszcza się do funkcji stałej równej 1)

Tłumaczenie własności funkcji wykładniczej najłatwiej będzie zacząć od przedstawienia tego, jak wygląda wykres tej funkcji.

Wykresem funkcji wykładniczej jest krzywa, która zawsze przetnie oś OY w punkcie 1.
Pierwszą i najważniejszą rzeczą, którą należy ustalić przy rysowaniu funkcji wykładniczej, to czy $a>1,$ czy też $a<1.$

$(1)$Zacznijmy od sytuacji, gdy $a>1.$
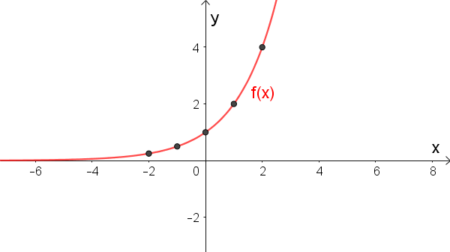
Dla przykładu narysujemy wykres funkcji $f(x)=2^{x}.$
W tym celu sporządzimy tabelkę:

x -2 -1 0 1 2
f(x) $\frac{1}{4}$ $\frac{1}{2}$ 1 2 4

Stąd otrzymujemy:

$(2)$ Teraz zajmiemy się przypadkiem, gdy $a<1.$

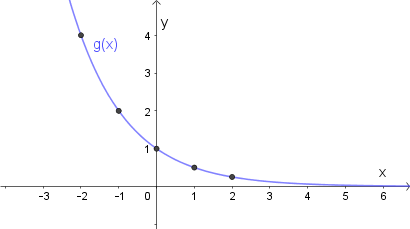
Dla przykładu narysujemy teraz wykres funkcji $g(x)=(\frac{1}{2})^{x}.$
Ponownie tworzymy tabelkę:

x -2 -1 0 1 2
g(x) 4 2 1 $\frac{1}{2}$ $\frac{1}{4}$

Stąd mamy:

Bardziej ogólne zachowanie wykresów funkcji wykładniczej przedstawiają poszczególne gify:

$(1)$ Gdy $a>1$

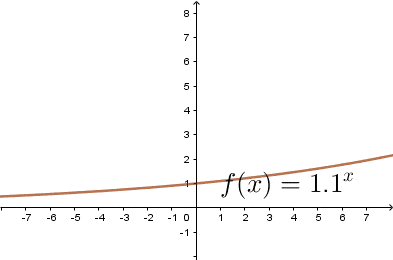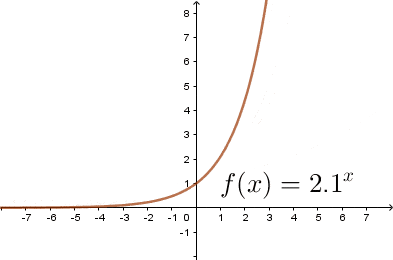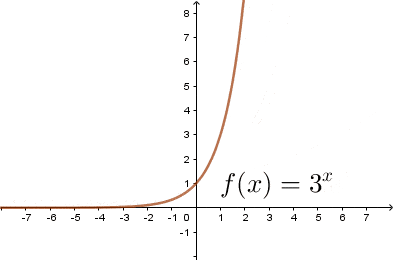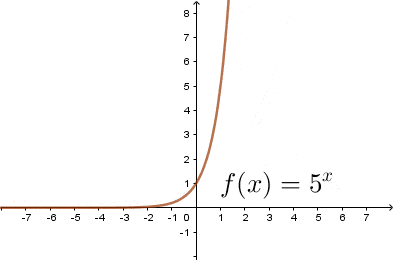
$(2)$ Gdy $a<1$

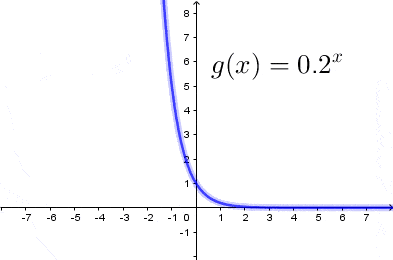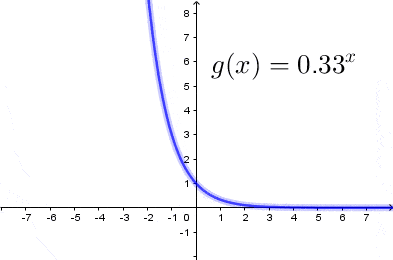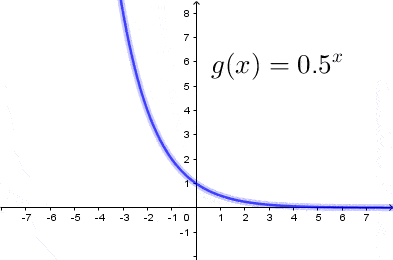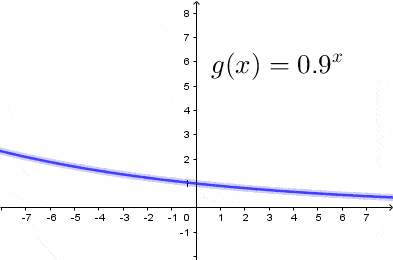
Z powyższych rysunków ławo odczytać następujące własności funkcji wykładniczej:

  1. Dziedziną funkcji wykładniczej są wszystkie liczby rzeczywiste, czyli zbiór $\mathbb{R}.$
  2. Funkcja wykładnicza przyjmuje tylko wartości dodatnie, tzn. zbiorem wartości tej funkcji jest zbiór $(0,\infty).$
  3. Dla argumentu 0 wartość funkcji jest zawsze równa 1.
  4. Funkcja wykładnicza jest:
    • Ściśle rosnąca, gdy $a>1$
    • Ściśle malejąca, gdy $a<1$
  5. Funkcja wykładnicza nie posiada miejsc zerowych (o ile jej nie przesuniemy w pionie)
Przykład 1: Na rysunku przedstawiony jest wykres funkcji wykładniczej $f(x)=a^{x}$ dla $x\in \mathbb{R}$, oblicz a.
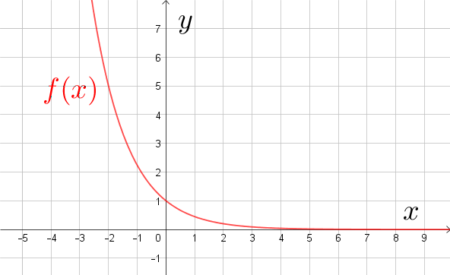
funkcja wykładnicza przykład1
Z rysunku odczytujemy, że punkt $(-2,5)$ należy do wykresu funkcji, zatem:
$f(-2)=5$
$a^{-2}=5$
$\frac{1}{a^2}=5$
$a^2=\frac{1}{5}$
$a=\sqrt{\frac{1}{5}} \quad \vee \quad a=-\sqrt{\frac{1}{5}}$
Ale z definicji funkcji wykładniczej pamiętamy, że $a>0,$ zatem:
$a=\sqrt{\frac{1}{5}}=\frac{1}{\sqrt{5}}=\frac{\sqrt{5}}{5}$
Odpowiedź: $a=\frac{\sqrt{5}}{5}.$
Przykład 2: Wiemy, że funkcja wykładnicza o równaniu: $f(x)=2^x$ przechodzi przez punkt $(4,b)$. Znajdź $b$.
Szukamy wartości funkcji f w punkcie $x=4$, czyli $b=f(4)$ zatem do wzoru funkcji podstawiamy:
$f(4)=2^4$
$f(4)=16$
Ponieważ $f(4)=b$, więc $b=16.$
Odpowiedź: $b=16.$
Przykład 3: Wyznacz zbiór wartości funkcji wykładniczej określonej wzorem $f(x)=3^x$ dla $x \in (-2,4>.$
Zauważmy, że funkcja określona w zadaniu jest ściśle rosnąca, ponieważ podstawa potęgi jest większa od 1. Wystarczy zatem policzyć wartości funkcji dla $x=-2$ oraz $x=4.$
$f(-2)=\frac{1}{9}$
$f(4)=81$
Odpowiedź: Zbiór wartości funkcji to przedział $(\frac{1}{9},81>.$
14+
Tobiasz Tomaszewski