Mamy 2 widgety dotyczące postaci kierunkowej i postaci ogólnej funkcji liniowej.
1) W pierwszym mamy podaną postać kierunkową prostej.
a) Odczytaj jaki jest współczynnik kierunkowy $a$ (czy jest dodatni, ujemny bądź równy $0$) i ustal jaka jest funkcja (rosnąca, malejąca bądź stała)
b) Następnie sprawdź przez który z podanych punktów przechodzi wykres podanej funkcji.
Uwaga: Więcej zagadnień matematycznych odnoszących się do poniższych zadań znajdziesz na stronie wzór funkcji liniowej.
2) Zaś w drugim widgecie mamy podaną postać ogólną prostej.
a) Odczytaj, który ze współczynników jest równy $0$.
b) Na tej podstawie wywnioskuj jaką własność ma podana funkcja.
Funkcja liniowa
Funkcją liniową nazywamy funkcję $f$ określoną wzorem:
$$\Large{y={\color[rgb]{0.9, 0.0, 0.45}a} \cdot x + {\color[rgb]{0.2, 0.2, 0.6}b}}$$gdzie ${\color[rgb]{0.9, 0.0, 0.45}a}$, ${\color[rgb]{0.2, 0.2, 0.6}b}$ $\in\mathbb{R}$ oraz
$$\Large{y={\color[rgb]{0.9, 0.0, 0.45}a} \cdot x + {\color[rgb]{0.2, 0.2, 0.6}b}}$$gdzie ${\color[rgb]{0.9, 0.0, 0.45}a}$, ${\color[rgb]{0.2, 0.2, 0.6}b}$ $\in\mathbb{R}$ oraz
- ${\color[rgb]{0.9, 0.0, 0.45}a}$ nazywamy ${\color[rgb]{0.9, 0.0, 0.45}współczynnikiem}$ ${\color[rgb]{0.9, 0.0, 0.45}kierunkowym}$ ${\color[rgb]{0.9, 0.0, 0.45} prostej}$
- ${\color[rgb]{0.2, 0.2, 0.6}b}$ nazywamy ${\color[rgb]{0.2, 0.2, 0.6}wyrazem}$ ${\color[rgb]{0.2, 0.2, 0.6}wolnym}$
Równanie kierunkowe prostej a równanie ogólne
Uwaga: Możemy spotkać się z takim zapisem:
- $y={\color[rgb]{0.9, 0.0, 0.45}a} \cdot x + {\color[rgb]{0.2, 0.2, 0.6}b}$ i jest to równanie kierunkowe prostej
- $Ax + By + C=0$ i jest to równanie ogólne prostej, gdzie $A^2 +B^2 \neq 0$ tj. współczynniki $A$ i $B$ nie są równocześnie równe $0$
Co możemy odczytać z postaci $y=a \cdot x + b$ ?
- Liczba ${\color[rgb]{0.9, 0.0, 0.45}a}$ to współczynnik kierunkowy prostej
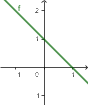
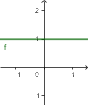
- Funkcja liniowa jest
| malejąca | stała | rosnąca |
 |
 |
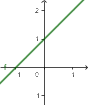 |
| ${\color[rgb]{0.9, 0.0, 0.45}a}<0$ | ${\color[rgb]{0.9, 0.0, 0.45}a}=0$ | ${\color[rgb]{0.9, 0.0, 0.45}a}>0$ |
Co możemy odczytać z równania ogólnego prostej $Ax + By + C=0$ ?
| Jeżeli | $A=0$ | to prosta | jest równoległa do osi OX |  |
| $B=0$ | jest równoległa do osi OY |  |
||
| $C=0$ | przechodzi przez początek układu współrzędnych czyli punkt $(0, 0)$ |
 |
1+
