Kąt środkowy i wpisany
Najpierw wyjaśnimy czym jest kąt środkowy i wpisany.
Kąt środkowy w okręgu jest to kąt, którego wierzchołkiem jest środek tego okręgu (na rysunku zaznaczyliśmy kąt środkowy oparty na łuku ACB).

Kąt wpisany w okrąg jest to taki wypukły kąt, którego wierzchołek leży na okręgu, a ramiona zawierają cięciwy okręgu (na rysunku zaznaczyliśmy kąt wpisany w okrąg oparty na łuku ACB).

Własności kąta środkowego i wpisanego
Uwaga: To jest w karcie wzorów! Wiele prostych zadań można rozwiązać za pomocą tych własności.
Zachodzą następujące własności:
- Kąt wpisany w okręg jest równy połowie kąta środkowego opartego na tym samym łuku.
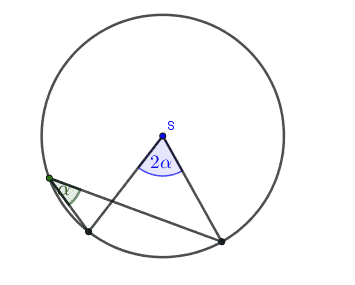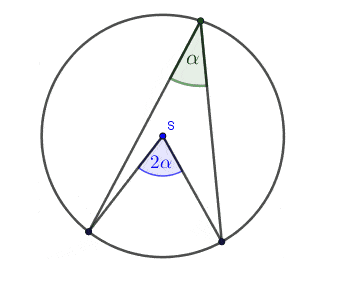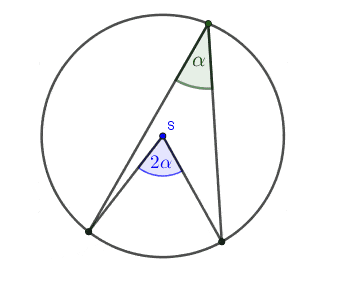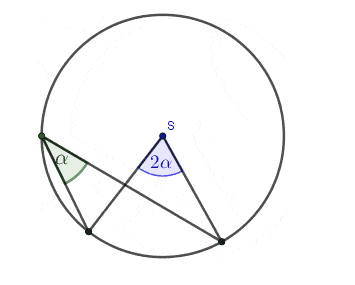
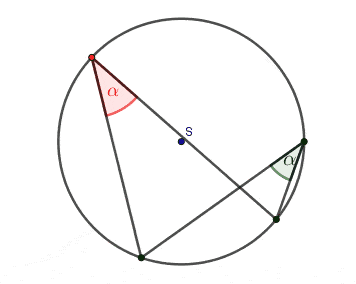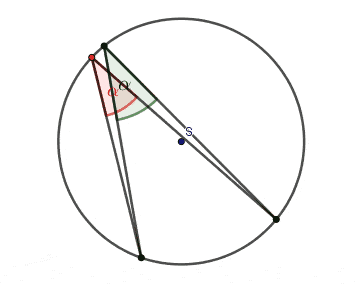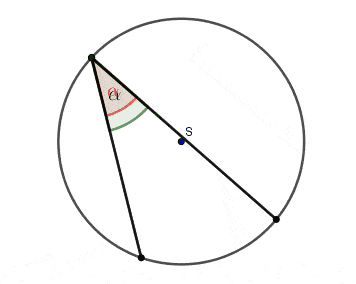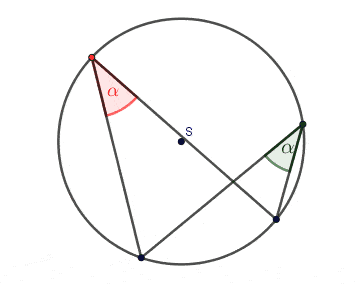
- Kąty wpisane oparte na tym samym łuku są równe.
- Kąt wpisany oparty na półokręgu jest kątem prostym.
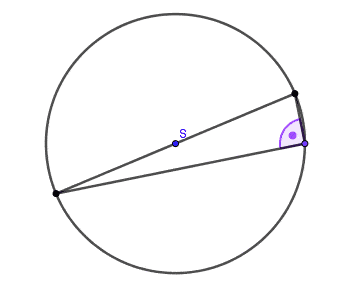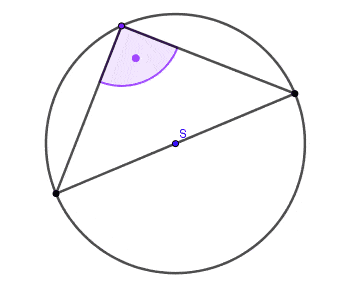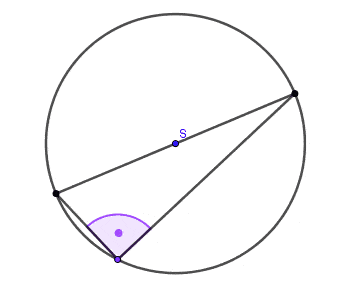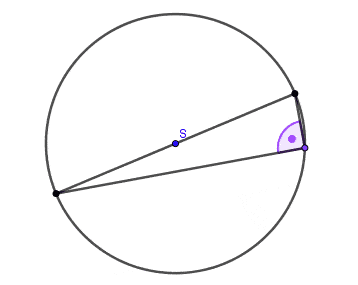 Wniosek: Każdy trójkąt wpisany w okrąg, którego jeden bok jest średnicą tego okręgu, jest trójkątem prostokątnym.
Wniosek: Każdy trójkąt wpisany w okrąg, którego jeden bok jest średnicą tego okręgu, jest trójkątem prostokątnym.
Przykłady
Rozwiązanie:
Skorzystamy z następującej własności:

Z treści zadania wiemy, że $\beta=30^\circ$. Zatem $\gamma=2\beta=2\cdot 30^\circ=60^\circ$.

Zatem skoro $\gamma=60^\circ$, to $\alpha=360^\circ-\gamma=360^\circ-60^\circ=300^\circ$.

Odpowiedź: Miara kąta $\alpha$ wynosi $300^\circ$.
Skorzystamy z następującej własności:
Z treści zadania wiemy, że $\beta=30^\circ$. Zatem $\gamma=2\beta=2\cdot 30^\circ=60^\circ$.
Zatem skoro $\gamma=60^\circ$, to $\alpha=360^\circ-\gamma=360^\circ-60^\circ=300^\circ$.
Odpowiedź: Miara kąta $\alpha$ wynosi $300^\circ$.
Przykład 2: Znajdź miarę kąta $\alpha$ jeśli $\gamma$ ma $110^\circ$.

Rozwiązanie:
Z treści zadania wiemy, że $\gamma=110^\circ$. Zatem $\beta=360^\circ-\gamma=360^\circ-110^\circ=250^\circ$.

Teraz skorzystamy z następującej własności:

Skoro $\beta=250^\circ$, to $\alpha=\frac{\beta}{2}=\frac{250^\circ}{2}=125^\circ$.

Odpowiedź: Miara kąta $\alpha$ wynosi $125^\circ$.
Z treści zadania wiemy, że $\gamma=110^\circ$. Zatem $\beta=360^\circ-\gamma=360^\circ-110^\circ=250^\circ$.
Teraz skorzystamy z następującej własności:
Skoro $\beta=250^\circ$, to $\alpha=\frac{\beta}{2}=\frac{250^\circ}{2}=125^\circ$.
Odpowiedź: Miara kąta $\alpha$ wynosi $125^\circ$.
Rozwiązanie:
Wiemy z treści zadania, że $\beta=90^\circ$ oraz $\gamma=60^\circ$.

Najpierw obliczymy miarę kąta $\delta$, wiedząc, że suma miar kątów w trójkącie jest równa $180^\circ$. Zatem
$\delta=180^\circ-\beta-\gamma=180^\circ-90^\circ-60^\circ=30^\circ$.

Teraz skorzystamy z następującej własności:

Zatem $\alpha=\delta=30^\circ$.

Odpowiedź: Miara kąta $\alpha$ wynosi $30^\circ$.
Wiemy z treści zadania, że $\beta=90^\circ$ oraz $\gamma=60^\circ$.
Najpierw obliczymy miarę kąta $\delta$, wiedząc, że suma miar kątów w trójkącie jest równa $180^\circ$. Zatem
$\delta=180^\circ-\beta-\gamma=180^\circ-90^\circ-60^\circ=30^\circ$.
Teraz skorzystamy z następującej własności:
Zatem $\alpha=\delta=30^\circ$.
Odpowiedź: Miara kąta $\alpha$ wynosi $30^\circ$.
Rozwiązanie:
Skorzystamy z następującej własności:

Z treści zadania wiemy, że $\beta=100^\circ$. Zatem $\alpha=\frac{\beta}{2}=\frac{100^\circ}{2}=50^\circ$.

Odpowiedź: Miara kąta $\alpha$ wynosi $50^\circ$.
Skorzystamy z następującej własności:
Z treści zadania wiemy, że $\beta=100^\circ$. Zatem $\alpha=\frac{\beta}{2}=\frac{100^\circ}{2}=50^\circ$.
Odpowiedź: Miara kąta $\alpha$ wynosi $50^\circ$.
Przykład 5: Wiedząc, że miary kątów trójkąta ABC wpisanego w okrąg wynoszą: $|\measuredangle{BAC}|=40^\circ$, $|\measuredangle{ABC}|=70^\circ$, wyznacz miarę kąta środkowego ASB.
Rozwiązanie:

Mamy wyznaczyć miarę kąta $\alpha$. Najpierw obliczmy miarę kąta $\beta$ wiedząc, że suma miar kątów w trójkącie jest równa $180^\circ$. Zatem
$\beta=180^\circ-(40^\circ+70^\circ)=70^\circ$

Teraz skorzystamy z następującej własności:

Otrzymujemy, że $\alpha=2\beta=2\cdot 70^\circ=140^\circ$.

Odpowiedź: Miara kąta środkowego ASB wynosi $140^\circ$.
Mamy wyznaczyć miarę kąta $\alpha$. Najpierw obliczmy miarę kąta $\beta$ wiedząc, że suma miar kątów w trójkącie jest równa $180^\circ$. Zatem
$\beta=180^\circ-(40^\circ+70^\circ)=70^\circ$
Teraz skorzystamy z następującej własności:
Otrzymujemy, że $\alpha=2\beta=2\cdot 70^\circ=140^\circ$.
Odpowiedź: Miara kąta środkowego ASB wynosi $140^\circ$.
Więcej przykładów
Przykład 6: Punkt O jest środkiem okręgu. Dane są: $|\measuredangle{ADC}|=55^\circ$, $|\measuredangle{DOB}|=150^\circ$. Wyznacz miary kątów czworokąta ABCD.

Rozwiązanie:

Kąty $\sphericalangle{BAD}$ i $\sphericalangle{BOD}$ są odpowiedni kątami wpisanym i środkowym i są oparte na tym samym łuku okręgu (zaznaczonym na rysunku kolorem czerwonym). Dlatego
$\alpha=\frac{1}{2}\cdot150^\circ$
$\alpha=75^\circ$
Podobnie obliczamy kąt $\sphericalangle{BCD}$:
$\gamma=\frac{1}{2}\cdot(360^\circ-150^\circ)$
$\gamma=\frac{1}{2}\cdot210^\circ$
$\gamma=105^\circ$
Miarę kąta $\sphericalangle{ABC}$ obliczymy wiedząc, że suma miar kątów w czworokącie jest równa $360^\circ$.
$\beta=360^\circ-(\alpha+\gamma+55^\circ)$
$\beta=360^\circ-(75^\circ+105^\circ+55^\circ)$
$\beta=360^\circ-235^\circ$
$\beta=125^\circ$
Odpowiedź: Miary kątów czworokąta ABCD wynoszą: $75^\circ$, $125^\circ$, $105^\circ$, $55^\circ$.
Kąty $\sphericalangle{BAD}$ i $\sphericalangle{BOD}$ są odpowiedni kątami wpisanym i środkowym i są oparte na tym samym łuku okręgu (zaznaczonym na rysunku kolorem czerwonym). Dlatego
$\alpha=\frac{1}{2}\cdot150^\circ$
$\alpha=75^\circ$
Podobnie obliczamy kąt $\sphericalangle{BCD}$:
$\gamma=\frac{1}{2}\cdot(360^\circ-150^\circ)$
$\gamma=\frac{1}{2}\cdot210^\circ$
$\gamma=105^\circ$
Miarę kąta $\sphericalangle{ABC}$ obliczymy wiedząc, że suma miar kątów w czworokącie jest równa $360^\circ$.
$\beta=360^\circ-(\alpha+\gamma+55^\circ)$
$\beta=360^\circ-(75^\circ+105^\circ+55^\circ)$
$\beta=360^\circ-235^\circ$
$\beta=125^\circ$
Odpowiedź: Miary kątów czworokąta ABCD wynoszą: $75^\circ$, $125^\circ$, $105^\circ$, $55^\circ$.
Przykład 7: Kąt wpisany w okrąg o środku S, oparty na łuku AB, ma miarę $30^\circ$. Oblicz miary kątów trójkąta ABS.
Rozwiązanie:

Kąty $\sphericalangle{ACB}$ i $\sphericalangle{ASB}$ są odpowiedni kątem wpisanym w okrąg i kątem środkowym okręgu i są oparte na tym samym łuku AB, dlatego $\alpha=2\cdot30^\circ=60^\circ$.
Trójkąt ABS jest równoramienny, dlatego $\beta=\gamma$. Zatem:
$\alpha+\beta+\gamma=180^\circ$
$60^\circ+\beta+\beta=180^\circ=180^\circ$
$2\beta=120^\circ$
$\beta=60^\circ=\gamma$
Odpowiedź: Trójkąt ABS jest trójkątem równobocznym, czyli wszystkie jego kąty mają miarę $60^\circ$.
Kąty $\sphericalangle{ACB}$ i $\sphericalangle{ASB}$ są odpowiedni kątem wpisanym w okrąg i kątem środkowym okręgu i są oparte na tym samym łuku AB, dlatego $\alpha=2\cdot30^\circ=60^\circ$.
Trójkąt ABS jest równoramienny, dlatego $\beta=\gamma$. Zatem:
$\alpha+\beta+\gamma=180^\circ$
$60^\circ+\beta+\beta=180^\circ=180^\circ$
$2\beta=120^\circ$
$\beta=60^\circ=\gamma$
Odpowiedź: Trójkąt ABS jest trójkątem równobocznym, czyli wszystkie jego kąty mają miarę $60^\circ$.
Rozwiązanie:

Kąty $\sphericalangle{ADB}$ i $\sphericalangle{ACB}$ są kątami wpisanymi w okrąg i są oparte na tym samym łuku okręgu (zaznaczonym kolorem czerwonym na rysunku). Dlatego $\beta=60^\circ$.
W trójkącie ADB:
$\alpha+\beta+90^\circ=180^\circ$
$\alpha=90^\circ-\beta$
$\alpha=90^\circ-60^\circ$
$\alpha=30^\circ$
Odpowiedź: Miara kąta $\alpha$ wynosi $30^\circ$.
Kąty $\sphericalangle{ADB}$ i $\sphericalangle{ACB}$ są kątami wpisanymi w okrąg i są oparte na tym samym łuku okręgu (zaznaczonym kolorem czerwonym na rysunku). Dlatego $\beta=60^\circ$.
W trójkącie ADB:
$\alpha+\beta+90^\circ=180^\circ$
$\alpha=90^\circ-\beta$
$\alpha=90^\circ-60^\circ$
$\alpha=30^\circ$
Odpowiedź: Miara kąta $\alpha$ wynosi $30^\circ$.
Przykład 9: W okrąg o promieniu długości $r=\sqrt{13}$ cm wpisano trójkąt prostokątny, którego jedna przyprostokątna jest dwa razy dłuższa od drugiej. Oblicz obwód i pole tego trójkąta.
Rozwiązanie:
Jeżeli trójkąt prostokątny jest wpisany w okrąg, to przeciwprostokątna trójkąta jest średnicą okręgu. Więcej o trójkącie prostokątnym napisaliśmy tutaj.

Najpierw obliczymy x z twierdzenia Pitagorasa:
$x^2+(2x)^2=(2r)^2$
$x^2+4x^2=(2\sqrt{13})^2$
$5x^2=4\cdot13$
$x^2=\frac{4\cdot13}{5}$
$x=\frac{2\sqrt{13}}{\sqrt{5}}$
$x=\frac{2\sqrt{13}\cdot\sqrt{5}}{5}$
$x=\frac{2}{5}\sqrt{65}$
Teraz obliczymy obwód trójkąta:
$l=3x+2r$
$l=3\cdot\frac{2}{5}\sqrt{65}+2\sqrt{13}$
$l=\frac{6}{5}\sqrt{65}+2\sqrt{13}$
Policzmy pole trójkąta:
$P=\frac{1}{2}x\cdot2x$
$P=x^2$
$P=\frac{4\cdot13}{5}$
$P=\frac{52}{5}$
Odpowiedź: Obwód trójkąta wynosi $\frac{6}{5}\sqrt{65}+2\sqrt{13}$ $cm$, zaś pole $\frac{52}{5}$ $cm^2$.
Jeżeli trójkąt prostokątny jest wpisany w okrąg, to przeciwprostokątna trójkąta jest średnicą okręgu. Więcej o trójkącie prostokątnym napisaliśmy tutaj.
Najpierw obliczymy x z twierdzenia Pitagorasa:
$x^2+(2x)^2=(2r)^2$
$x^2+4x^2=(2\sqrt{13})^2$
$5x^2=4\cdot13$
$x^2=\frac{4\cdot13}{5}$
$x=\frac{2\sqrt{13}}{\sqrt{5}}$
$x=\frac{2\sqrt{13}\cdot\sqrt{5}}{5}$
$x=\frac{2}{5}\sqrt{65}$
Teraz obliczymy obwód trójkąta:
$l=3x+2r$
$l=3\cdot\frac{2}{5}\sqrt{65}+2\sqrt{13}$
$l=\frac{6}{5}\sqrt{65}+2\sqrt{13}$
Policzmy pole trójkąta:
$P=\frac{1}{2}x\cdot2x$
$P=x^2$
$P=\frac{4\cdot13}{5}$
$P=\frac{52}{5}$
Odpowiedź: Obwód trójkąta wynosi $\frac{6}{5}\sqrt{65}+2\sqrt{13}$ $cm$, zaś pole $\frac{52}{5}$ $cm^2$.
28+
