Miejsca zerowe – przypomnienie
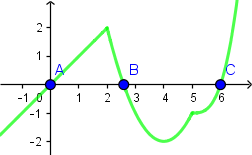
Zaznaczone punkty to miejsca zerowe narysowanej funkcji.
Ilość miejsc zerowych funkcji kwadratowej
Funkcja kwadratowa może mieć:
|
 |
|
 |
|
 |
Przykład: $f(x)=-x^2+4x-4$
$a=-1,\;b=4,\;c=-4$
$\Delta=b^2-4ac=4^2-4\cdot(-1)\cdot(-4)$$=16-16=0$
$\Delta=0$, więc funkcja $f(x)=-x^2+4x-4$ ma jedno miejsce zerowe.
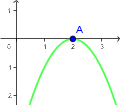
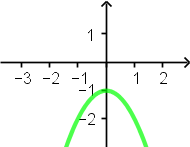
Jest jeden punkt, w którym wykres styka się z osią $OX$. Jest to jedyne miejsce zerowe funkcji.
Przykład: $f(x)=2x^2+4x+3$
$a=2,\;b=4,\;c=3$
$\Delta$$=b^2-4ac$$=4^2-4\cdot2\cdot3$$=16-24=-8$
$\Delta<0$, więc funkcja $f(x)=2x^2+4x+3$ nie ma miejsc zerowych.
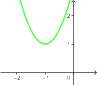
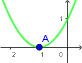
Wykres jest całkowicie ponad osią $OX$, nie przecina się z nią. Widzimy, że nie ma miejsc zerowych.
Miejsca zerowe funkcji kwadratowej
Teraz nauczymy się liczyć miejsca zerowe funkcji kwadratowej.
Jeśli $\boldsymbol\Delta\boldsymbol>\mathbf0$, czyli funkcja ma dwa miejsca zerowe $x_1$, $x_2$ to mamy wzory na obliczenie tych miejsc zerowych $x_1$, $x_2$:
Jeśli $\boldsymbol\Delta\boldsymbol=\mathbf0$, czyli funkcja ma jedno miejsce zerowe $x_0$, to $x_0$ nazywamy pierwiastkiem podwójnym i liczymy ze wzoru:
$$\Large{x_{0}=\frac{-b}{2a}}$$
Dlatego $x_0$ nazywamy pierwiastkiem podwójnym, bo $x_1=x_2=\frac{-b}{2a}$.
Przykłady
Przykład: $f(x)=x^2+6x+5$
$a=1,\;b=6,\;c=5$
$\Delta=b^2-4ac=6^2-4\cdot1\cdot5$$=36-20=16$
$\Delta>0$, więc są dwa miejsca zerowe. Liczymy je z podanych wzorów.
$\sqrt\Delta=\sqrt{16}=4$
$x_1=\frac{-b-\sqrt\Delta}{2a}=\frac{-6-4}{2\cdot1}=\frac{-10}2=-5$
$x_2=\frac{-b+\sqrt\Delta}{2a}=\frac{-6+4}{2\cdot1}=\frac{-2}2=-1$
Liczby $-5$ i $-1$ są miejscami zerowymi funkcji $f(x)=x^2+6x+5$.
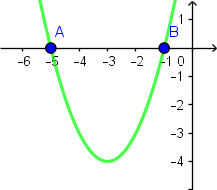
Na wykresie widzimy, że dla $x=-5$ i $x=-1$ funkcja osiąga wartość $0$, czyli mamy tam miejsca zerowe.
Przykład: $f(x)=-x^2+4x-4$
$a=-1,\;b=4,\;c=-4$
$\Delta=b^2-4ac=4^2-4\cdot(-1)\cdot(-4)$$=16-16=0$
$\Delta=0$, więc jest jedno miejsce zerowe.
$x_0=\frac{-b}{2a}=\frac{-4}{2\cdot(-1)}=\frac{-4}{-2}=2$
Liczba $2$ jest miejscem zerowym funkcji $f(x)=-x^2+4x-4$
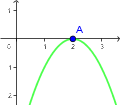
Na wykresie widać, że jest jedno miejsce zerowe $x=2$.
Przykład: $f(x)=2x^2+4x+3$
$a=2,\;b=4,\;c=3$
$\Delta=b^2-4ac=4^2-4\cdot2\cdot3$$=16-24=-8$
$\Delta<0$, więc funkcja nie ma miejsc zerowych.
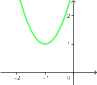
Na wykresie widać, że funkcja nie przecina osi $OX$, czyli nie ma miejsc zerowych.
Przykład: $f(x)=-2x^2+9x+5$
$a=-2,\;b=9,\;c=5$
$\Delta=b^2-4ac=9^2-4\cdot(-2)\cdot5$$=81+40=121$
$\Delta>0$. Mamy dwa miejsca zerowe.
$\sqrt\Delta=\sqrt{121}=11$
$x_1=\frac{-b-\sqrt\Delta}{2a}=\frac{-9-11}{2\cdot(-2)}=\frac{-20}{-4}=5$
$x_2=\frac{-b+\sqrt\Delta}{2a}=\frac{-9+11}{2\cdot(-2)}=\frac{2}{-4}=-\frac12$
Liczby $5$ i $-\frac12$ są miejscami zerowymi funkcji $f$.
Przykład: $f(x)=\frac13x^2-\frac13x+\frac1{12}$
$a=\frac13,\;b=\frac13,\;c=\frac1{12}$
$\Delta=b^2-4ac=\left(\frac13\right)^2-4\cdot\frac13\cdot\frac1{12}$$=\frac19-\frac19=0$
$\Delta=0$. Mamy jedno miejsce zerowe.
$x_0=\frac{-b}{2a}=\frac{-\frac13}{2\cdot\frac13}=\frac{-\frac13}{\frac23}$$=-\frac13\cdot\frac32=-\frac12$
Liczba $-\frac12$ jest podwójnym miejscem zerowym funkcji $f$.
Przykład: $f(x)=3x^2+2\sqrt5x+\frac74$
$a=3,\;b=2\sqrt5,\;c=\frac74$
$\Delta=b^2-4ac=\left(2\sqrt5\right)^2-4\cdot3\cdot\frac74$$=4\cdot5-3\cdot7=20-21=-1$
$\Delta<0$, więc funkcja nie ma miejsc zerowych.
Postać iloczynowa funkcji kwadratowej
Funkcję kwadratową w postaci ogólnej $f(x)=ax^2+bx+c$ możemy zapisać w postaci iloczynowej:
Jeśli $\Delta\geq0$. $x_1$ i $x_2$ to liczby są miejscami zerowymi funkcji $f$. Jeśli $\Delta<0$ to postać iloczynowa nie istnieje.
Współczynnik $a$ w postaci ogólnej i postaci iloczynowej jest taki sam.
Przykład: Zapisz wzór funkcji kwadratowej $f(x)=3x^2-7x-6$ w postaci iloczynowej, jeśli to możliwe.
Liczymy deltę:
$\Delta=b^2-4ac=7^2-4\cdot3\cdot(-6)$$=49+72=121$
$\Delta>0$, więc postać iloczynowa istnieje.
Obliczamy miejsca zerowe:
$x_1=\frac{-b-\sqrt\Delta}{2a}=\frac{7-11}{2\cdot3}=\frac{-4}6=-\frac23$
$x_2=\frac{-b-\sqrt\Delta}{2a}=\frac{7+11}{2\cdot3}=\frac{18}6=3$
Postać iloczynowa funkcji $f$:
$f(x)=3(x-(-\frac23))(x-3)$$=3(x+\frac23)(x-3)$
Przykład: Znajdź miejsca zerowe funkcji $f(x)=2(x-2)(x+5)$, która jest w postaci iloczynowej.
Więcej przykładów
Przykład: Oblicz miejsce zerowe funkcji kwadratowej $f(x)=(x+1)^2+4x+8$.
Widzimy, że nie jest podana postać ogólna funkcji kwadratowej. Najpierw musimy uporządkować wzór naszej funkcji, żeby móc znaleźć miejsca zerowe. Przekształcamy:
Uwaga na wzór skróconego mnożenia!
$f(x)=(x+1)^2+4x+8$$=x^2+2x+1+4x+8$$=x^2+6x+9$
Z takiej postaci liczymy deltę.
$\Delta=b^2-4ac=6^2-4\cdot1\cdot9$$=36-36=0$
Delta jest równa $0$, więc mamy jedno miejsce zerowe.
$x_0=\frac{-b}{2a}={-6}2=-3$
Liczba $-3$ jest podwójnym pierwiastkiem funkcji $f$.
Przykład: Dla jakich wartości parametru $m$ funkcja kwadratowa $f(x)=x^2+6x+2m-1$ ma dwa miejsca zerowe?
$a=1, b=6, c=2m-1$
$\Delta=b^2-4ac=m^2-4\cdot1\cdot(2m$$-1)=36-8m+4=40-8m$
Ustaliliśmy, że $\Delta>0$, żeby funkcja miała dwa miejsca zerowe, więc
$40-8m>0$
Przenosimy $8m$ na prawą stronę:
$40>8m$
Dzielimy stronami przez $8$:
$5>m$
Zatem delta jest dodatnia, gdy $m<5$.
Odpowiedź: Funkcja ma dwa miejsca zerowe dla $\boldsymbol m\boldsymbol<\mathbf5$.
Przykład: Sprawdź czy podane funkcje mają takie same miejsca zerowe $f(x)=2x^2+13x+15$, $g(x)=-\frac13(x+5)(x+1,5)$.
$\Delta=b^2-4ac=13^2-4\cdot2\cdot15$$=169-120=49$
$\sqrt\Delta=7$
$x_1=\frac{-b-\sqrt\Delta}{2a}=\frac{-13-7}{2\cdot2}=\frac{-20}4=-5$
$x_2=\frac{-b-\sqrt\Delta}{2a}=\frac{-13+7}{2\cdot2}=\frac{-6}4$$=-\frac32=-1,5$
Teraz przyjrzyjmy się funkcji $g$. Zauważmy, że jest zapisana w postaci iloczynowej, więc bez trudu możemy odczytać jej miejsca zerowe. Są nimi liczby $-5$ i $-1,5$.
Odpowiedź: Miejsca zerowe obu funkcji są takie same.
Przykład: Sprawdź czy funkcja kwadratowa $f(x)=-x^2+x+1$ ma miejsca zerowe przeciwnych znaków.
$\Delta=b^2-4ac=1^2-4\cdot(-1)\cdot1$$=1+4=5$
$\sqrt\Delta=\sqrt5$
$x_1=\frac{-b-\sqrt\Delta}{2a}=\frac{-1-\sqrt5}{2\cdot(-1)}=\frac{-1-\sqrt5}{-2}$$=\frac{1+\sqrt5}2>0$ (jest dodatnie, ponieważ dzielimy liczbę dodatnią przez liczbę dodatnią)
$x_2=\frac{-b-\sqrt\Delta}{2a}=\frac{-1+\sqrt5}{2\cdot(-1)}$$=\frac{-1+\sqrt5}{-2}<0$ (jest ujemne, ponieważ dzielimy liczbę dodatnią $-1+\sqrt5$ przez liczbę ujemną $-2$)
Odpowiedź: Funkcja ma miejsca zerowe różnych znaków – jedno ujemne, a drugie dodatnie.
Przykład: Miejscem zerowym funkcji $f(x)=-2x^2+2(k+1)x-k+3$ jest liczba $-1$. Znajdź $k$.
$0=-2\cdot(-1)^2+2(k+1)\cdot(-1)$$-k+3$
Rozwiązujemy równanie z niewiadomą $k$.
$0=-2-2k-2$$-k+3$
$0=-1-3k$
$3k=-1$
$k=-\frac13$
Odpowiedź: Otrzymujemy, że $k=-\frac{1}{3}$.
