Jak najłatwiej zdefiniować pojęcie “miejsce zerowe funkcji liniowej”?

Wyobraźmy sobie wykres dowolnej funkcji liniowej.

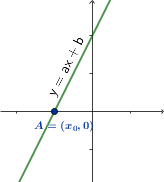
W większości przypadków wykres funkcji liniowej przecina oś $OX$ w punkcie $A=($$\color[rgb]{0.8, 0.2, 0.2}{\color[rgb]{0.8, 0.2, 0.2}x}_0$$, 0)$, gdzie $\color[rgb]{0.8, 0.2, 0.2}{\color[rgb]{0.8, 0.2, 0.2}x}_0$ jest miejscem zerowym.

Uwaga: Funkcja $y={\color[rgb]{0.9, 0.0, 0.45}a} \cdot x + {\color[rgb]{0.2, 0.2, 0.6}b}$ może nie mieć miejsca zerowego gdy jest stała, czyli ${\color[rgb]{0.9, 0.0, 0.45}a}=0$ lub w przypadku, gdy $y=0$ funkcja ma nieskończenie wiele miejsc zerowych (jej wykres pokrywa się z osią $OX$).

Miejsce zerowe funkcji liniowej możemy obliczyć na dwa sposoby:

  • Przyrównując wzór funkcji do zera.
  • Korzystając ze wzoru:
    $$\Large{\color[rgb]{0.8, 0.2, 0.2}{\color[rgb]{0.8, 0.2, 0.2}x}_0=\frac{-{\color[rgb]{0.2, 0.2, 0.6}b}}{\color[rgb]{0.9, 0.0, 0.45}a}}$$
    (wiedząc, że równanie ogólne prostej ma postać $y={\color[rgb]{0.9, 0.0, 0.45}a} \cdot x + {\color[rgb]{0.2, 0.2, 0.6}b}$).

Przykłady

Przykład: Wyznacz miejsce zerowe funkcji $y=2x+6$.

Przyrównujemy wzór funkcji do zera, czyli w miejsce $y$ wstawiamy $0$.
 

$y=2x+6$
$0=2x+6$ $|-2x$
$-2x=6$ $|:(-2)$
$x=3$

Odpowiedź: Miejscem zerowym funkcji $y=2x+6$ jest $\color[rgb]{0.8, 0.2, 0.2}{\color[rgb]{0.8, 0.2, 0.2}x}_0=3$.

Przykład: Wyznacz miejsce zerowe funkcji $y=2x+6$.

Aby skorzystać ze wzoru na miejsce zerowe $\color[rgb]{0.8, 0.2, 0.2}{\color[rgb]{0.8, 0.2, 0.2}x}_0$$=\frac{-{\color[rgb]{0.2, 0.2, 0.6}b}}{\color[rgb]{0.9, 0.0, 0.45}a}$ przypomnijmy ogólną postać równania prosteji porównajmy do danej, aby znaleźć $a$ i $b$. Mamy:
$y={\color[rgb]{0.9, 0.0, 0.45}a} \cdot x + {\color[rgb]{0.2, 0.2, 0.6}b}$
$y={\color[rgb]{0.9, 0.0, 0.45}2} \cdot x + {\color[rgb]{0.2, 0.2, 0.6}(-6)}$
Łatwo możemy zauważyć, że ${\color[rgb]{0.9, 0.0, 0.45}a}={\color[rgb]{0.9, 0.0, 0.45}2}$ i ${\color[rgb]{0.2, 0.2, 0.6}b}={\color[rgb]{0.2, 0.2, 0.6}(-6)}$. Podstawiamy do wzoru:
$\color[rgb]{0.8, 0.2, 0.2}{\color[rgb]{0.8, 0.2, 0.2}x}_0$=$\frac{-{\color[rgb]{0.2, 0.2, 0.6}b}}{\color[rgb]{0.9, 0.0, 0.45}a}$=$=\frac{-{\color[rgb]{0.2, 0.2, 0.6}(-6)}}{\color[rgb]{0.9, 0.0, 0.45}2}$=$\frac62=3$
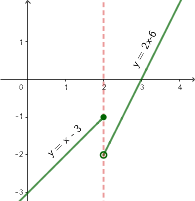
Odpowiedź: Miejscem zerowym funkcji $y=2x-6$ jest $x_0=3$.

Przykład: Funkcja $f$ określona jest wzorem: $f(x)=\left\{\begin{array}{l}x-3\;dla\;x\leqslant2\;\Leftrightarrow x\in(-\infty,2>\\2x-6\;dla\;x>2\;\Leftrightarrow x\in(2,\;+\infty)\end{array}\right.$. Ile miejsc zerowych ma ta funkcja?

Rozwiązując zadania tego typu możemy narysować wykres funkcji i odczytać z niego odpowiedź lub wyliczyć miejsca zerowe danych funkcji.
Z poniższego rysunku widać, że funkcja $f$ posiada jedno miejsce zerowe.

Aby zbadać istnienie miejsca zerowego/wyznaczyć miejsce zerowe przyrównamy wzory funkcji do zera:

$y=x-3$
$0=x-3$ $|-3$
$-x=-3$ $|:(-3)$
$x=3\not\in(-\infty,2>$
 

$x=3$ nie należy do danego przedziału, więc nie może być miejscem zerowym wynikającym ze wzoru funkcji $y=x-3$

 
$y=2x-6$
$0=2x-6$ $|-2x$
$-2x=-6$ $|:(-2)$
$x=3\in(2,\;+\infty)$
 

$x=3$ należy do danego przedziału, więc jest miejscem zerowym wynikającym ze wzoru funkcji $y=2x-6$

Odpowiedź: Wykorzystując oba sposoby udowodniliśmy, że funkcja $f$ ma jedno miejsce zerowe $x_0=3$.

Przykład: Liczba $2$ jest miejscem zerowym funkcji liniowej określonej wzorem $y=(\frac12m+3)x+1$. Znajdź $m$ i wyznacz dokładną postać równania kierunkowego prostej.

Rozwiązując to zadanie możemy użyć dowolnego z powyższych sposobów. Wykorzystamy sposób pierwszy. Spróbuj rozwiązać zadanie drugim sposobem 🙂

Przyrównamy wzór funkcji do $0$, a następnie skorzystamy z tego, że $\color[rgb]{0.8, 0.2, 0.2}{\color[rgb]{0.8, 0.2, 0.2}x}_0=2$.

$y=(\frac12m+3)x+1$
$0=(\frac12m+3)x+1$
$0=(\frac12m+3) \cdot {\color[rgb]{0.8, 0.2, 0.2}2}+1$  $|$Zamiana stron
 

$(\frac12m+3) \cdot {\color[rgb]{0.8, 0.2, 0.2}2}+1=0$
$\frac12m\cdot2 + 3\cdot2 +1=0$
$m+6+1=0$
$m+7=0$ $|-7$
$m=-7$

Wiemy już, że $m=-7$. Aby znaleźć wzór naszej funkcji wystarczy podstawić $m=-7$ do postaci z polecenia, czyli do $y=(\frac12m+3)x+1$.

$y=(\frac12\cdot(-7)+3)x+1$
$y=(-\frac72+3)x+1$
(wiemy, że $3\Leftrightarrow\frac62$)

$y=(-\frac72+\frac62)x+1$
$y=-\frac12x+1$

Odpowiedź: $m=-7$, $y=-\frac12x+1$.

Jak sprawdzić poprawność swojej odpowiedzi?

Skoro dla funkcji $y=-\frac12+1$ miejscem zerowym jest $\color[rgb]{0.8, 0.2, 0.2}{\color[rgb]{0.8, 0.2, 0.2}x}_0={\color[rgb]{0.8, 0.2, 0.2}2}$, to wartość funkcji w $x=2$ powinna wynosić $0$ $\Leftrightarrow$ $f(2)=0$. Sprawdzamy:

$y=-\frac12x+1$
$f({\color[rgb]{0.8, 0.2, 0.2}x})=-\frac12\cdot{\color[rgb]{0.8, 0.2, 0.2}2}+1$
$f({\color[rgb]{0.8, 0.2, 0.2}2})=-\frac12\cdot{\color[rgb]{0.8, 0.2, 0.2}2}+1$
$f(2)=(-1)+1$
$f(2)=0$

Zatem miejscem zerowym funkcji $f$ jest $2$.

Przykład: Funkcja liniowa $k$ określona wzorem $k:$ $2x+m$ ma takie samo miejsce zerowe jak funkcja liniowa $k$ określona wzorem $y=3x+9$. Wyznacz $m$.
Zacznijmy od znalezienia miejsca zerowego funkcji $l:$ $y=3x+9$. Widzimy, że $x_0=-\frac93=-3$
Z treści zadania wiemy, że jest to również miejsce zerowe funkcji $k$, czyli $k(-3)=0$.
Jest to jednoznaczne z tym, że:

 

$y=2x+m$
$0=2\cdot(-3)+m$
$0=-6+m$ $|-m$
$-m=-6$ $|:(-1)$
$m=6$

Odpowiedź: $m=6$.

1+
Anita Księżak