Ostrosłup prawidłowy czworokątny
Tworzenie ostrosłupów jest intuicyjnie nieco trudniejsze od tworzenia graniastosłupów, dlatego poza definicją formalną podamy krótki opis powstawania ostrosłupów krok po kroku.
Ostrosłup prawidłowy czworokątny to ostrosłup, który ma w podstawie kwadrat, a jego wysokość pada na punkt przecięcia się przekątnych tego kwadratu.
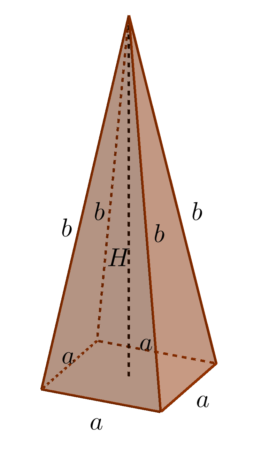

Jak powstaje ostrosłup prawidłowy czworokątny krok po kroku?
- Bierzemy dowolny kwadrat i zaznaczamy punkt przecięcia się jego przekątnych.
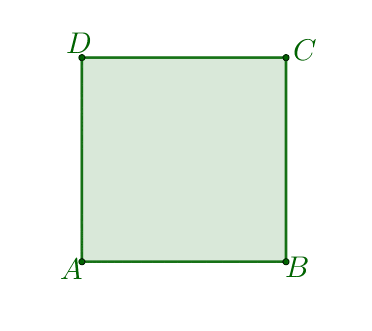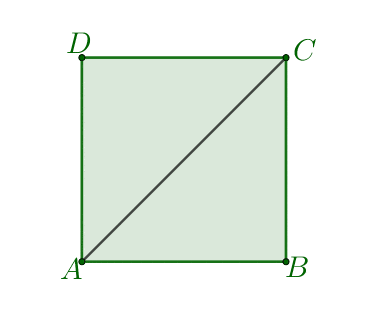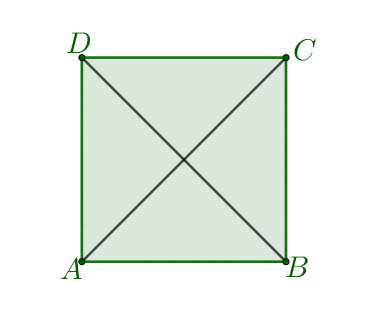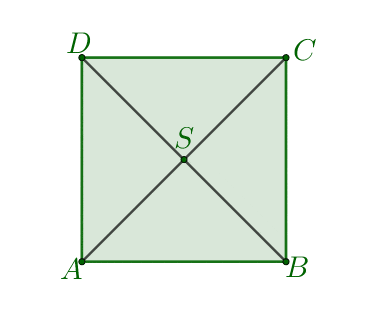
- Na prostej prostopadłej do płaszczyzny naszego kwadratu i przechodzącej przez punkt $S$ wybieramy punkt $W\neq S$. Tworzymy odcinki $AW,\: BW,\: CW,\: DW$ otrzymana w ten sposób bryła jest ostrosłupem prawidłowym czworokątnym.
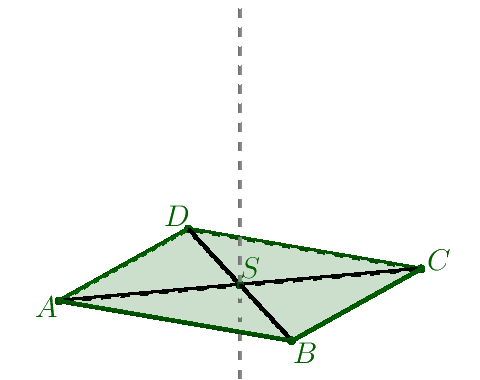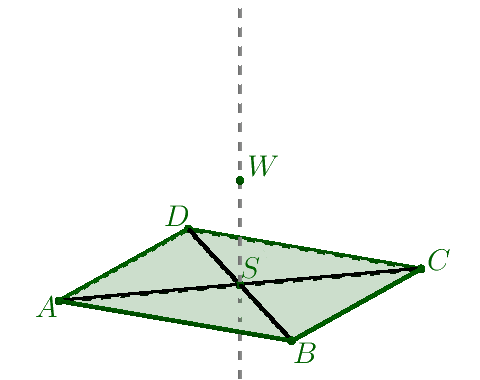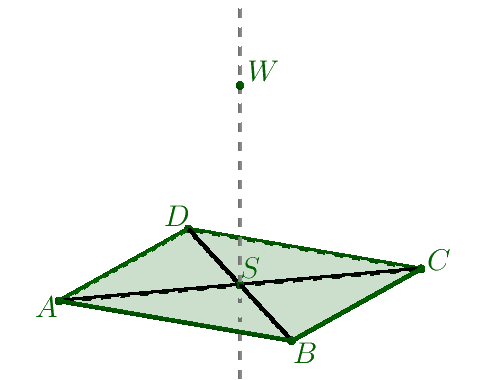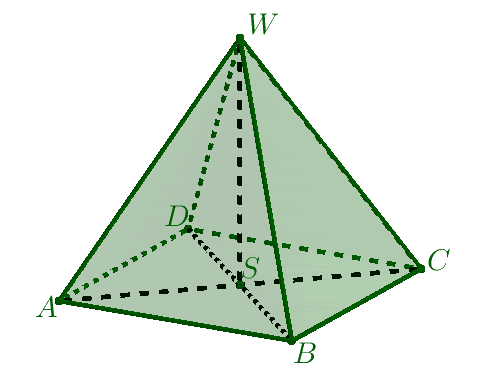
Zwróćmy uwagę na to, jak wygląda siatka ostrosłupa prawidłowego czworokątnego i jakie są jej wymiary:

Ostrosłup prawidłowy czworokątny ma zawsze:
- 5 ścian
- 8 krawędzi
- 5 wierzchołków
Objętość ostrosłupa prawidłowego czworokątnego
Objętość ostrosłupa wyraża się wzorem:
$V=\frac{1}{3}Pole\: podstawy\cdot wysokość\: ostrosłupa$
W przypadku ostrosłupa prawidłowego czworokątnego podstawą jest kwadrat, zatem
$Pole\: podstawy=a^2$
Ostatecznie mamy:
Objętość ostrosłupa prawidłowego czworokątnego wyraża się wzorem:
$$V=\frac{1}{3}a^{2}H$$
$$V=\frac{1}{3}a^{2}H$$
Pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego
Pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego można opisać na wiele sposobów w zależności od tego, jakie mamy dostępne dane. Poniżej pokażemy najczęściej zapisywaną formę tego wzoru.
Dla oznaczeń jak na rysunku, pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego określa wzór:
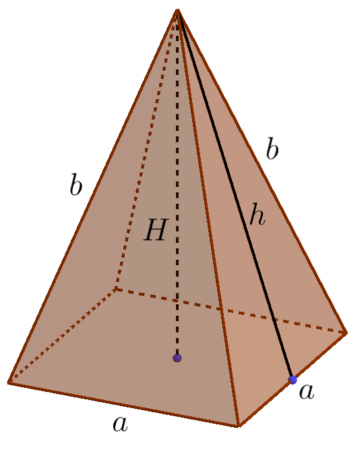

$$P_{C}=\underbrace{a^2}_{Pole\: podstawy}+\overbrace{4}^{4\: ściany\: boczne}\cdot \underbrace{\frac{1}{2}ah}_{Pole\: ściany\: bocznej}=a^2+2ah$$
Kąty w ostrosłupie prawidłowym czworokątnym
Przykład 1: Dany jest ostrosłup prawidłowy czworokątny, którego wszystkie krawędzie mają długość 12. Oblicz długość wysokości tego ostrosłupa.
Narysujmy obrazek poglądowy:
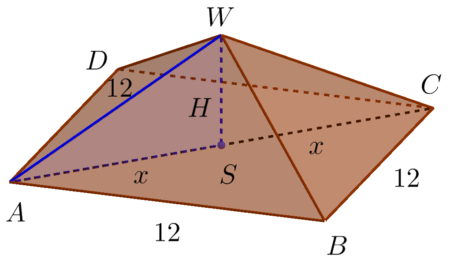
Ze wzoru na długość przekątnej kwadratu mamy:
$2x=12\sqrt{2}$
$x=6\sqrt2$
Natomiast z twierdzenia Pitagorasa dla trójkąta $SAW$ otrzymujemy:
$H^2+x^2=12^2$
$H^2=144-x^2=144-(6\sqrt2)^2=144-36\cdot 2=72$
$H=\sqrt{72} \quad \vee \quad H=-\sqrt{72}$
Odległość musi być nieujemna, zatem:
$H=\sqrt{72}=\sqrt{36\cdot 2}=6\sqrt2$
Odpowiedź:Wysokość tego ostrosłupa ma długość $6\sqrt2.$

Ze wzoru na długość przekątnej kwadratu mamy:
$2x=12\sqrt{2}$
$x=6\sqrt2$
Natomiast z twierdzenia Pitagorasa dla trójkąta $SAW$ otrzymujemy:
$H^2+x^2=12^2$
$H^2=144-x^2=144-(6\sqrt2)^2=144-36\cdot 2=72$
$H=\sqrt{72} \quad \vee \quad H=-\sqrt{72}$
Odległość musi być nieujemna, zatem:
$H=\sqrt{72}=\sqrt{36\cdot 2}=6\sqrt2$
Odpowiedź:Wysokość tego ostrosłupa ma długość $6\sqrt2.$
Przykład 2: W ostrosłupie prawidłowym czworokątnym prawidłowym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem $60^{\circ},$ a przekątna podstawy jest równa $\sqrt2 .$Oblicz objętość i pole powierzchni tego ostrosłupa.
Narysujmy obrazek poglądowy:
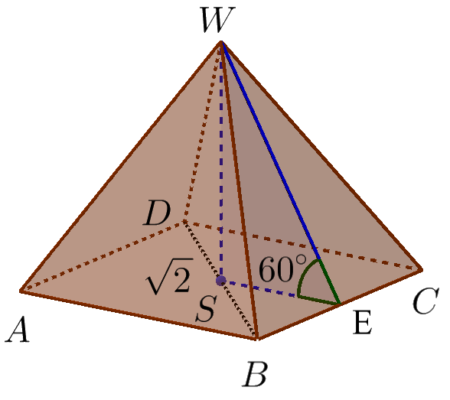
Ze wzoru na na długość przekątnej kwadratu możemy obliczyć długość odcinka $AB$
$\mid AB \mid \sqrt2 = \sqrt2$
$\mid AB \mid =1$
Zauważmy, że:
$\mid SE \mid =\frac{1}{2} \mid AB \mid$
Znając długość odcinka $SE$ możemy policzyć długość odcinka $SW,$ czyli wysokości naszego ostrosłupa.
$tg60^{\circ}=\frac{\mid SW \mid}{\mid SE \mid}$
$\sqrt{3}=\frac{\mid SW \mid}{\frac{1}{2}}$
$\mid SW \mid=\frac{1}{2}\sqrt3$
Policzmy dodatkowo długość odcinka $EW:$
$cos60^{\circ}=\frac{\mid SE \mid}{\mid WE \mid}$
$\frac{1}{2}=\frac{\frac{1}{2}}{\mid WE \mid}$
$\mid WE \mid =1$
Pozostało podstawić dane do wzorów na objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego:
$V=\frac{1}{3}\mid AB \mid \cdot \mid SW \mid=\frac{1}{3} \cdot 1 \cdot \frac{1}{2}\sqrt3= \frac{\sqrt3}{6}$
$P_{C}=\mid AB \mid ^2 +2\mid AB \mid \cdot \mid WE \mid=1^2+2\cdot 1 \cdot 1=3$
Odpowiedź: Objętość tego ostrosłupa, to $\frac{\sqrt3}{6},$ a jego pole powierzchni całkowitej, to $3.$

Ze wzoru na na długość przekątnej kwadratu możemy obliczyć długość odcinka $AB$
$\mid AB \mid \sqrt2 = \sqrt2$
$\mid AB \mid =1$
Zauważmy, że:
$\mid SE \mid =\frac{1}{2} \mid AB \mid$
Znając długość odcinka $SE$ możemy policzyć długość odcinka $SW,$ czyli wysokości naszego ostrosłupa.
$tg60^{\circ}=\frac{\mid SW \mid}{\mid SE \mid}$
$\sqrt{3}=\frac{\mid SW \mid}{\frac{1}{2}}$
$\mid SW \mid=\frac{1}{2}\sqrt3$
Policzmy dodatkowo długość odcinka $EW:$
$cos60^{\circ}=\frac{\mid SE \mid}{\mid WE \mid}$
$\frac{1}{2}=\frac{\frac{1}{2}}{\mid WE \mid}$
$\mid WE \mid =1$
Pozostało podstawić dane do wzorów na objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego:
$V=\frac{1}{3}\mid AB \mid \cdot \mid SW \mid=\frac{1}{3} \cdot 1 \cdot \frac{1}{2}\sqrt3= \frac{\sqrt3}{6}$
$P_{C}=\mid AB \mid ^2 +2\mid AB \mid \cdot \mid WE \mid=1^2+2\cdot 1 \cdot 1=3$
Odpowiedź: Objętość tego ostrosłupa, to $\frac{\sqrt3}{6},$ a jego pole powierzchni całkowitej, to $3.$
Przykład 3: W ostrosłupie prawidłowym czworokątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem $45^{\circ},$ a pole podstawy jest równe $16.$ Oblicz objętość tego ostrosłupa.
Narysujmy obrazek poglądowy:
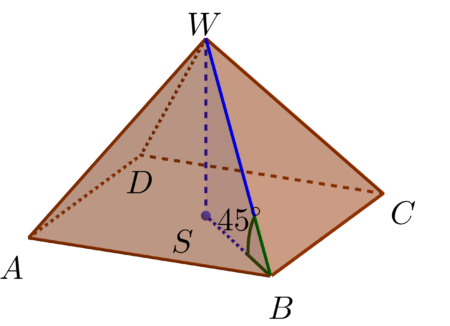
Narysujmy dodatkowo trójkąt $SBW:$

Wiemy, że $\mid AB \mid ^2 =16$
Zatem:
$\mid AB \mid=4 \quad \vee \quad \mid AB \mid=-4$
Odległość musi być nieujemna, zatem
$\mid AB \mid =4$
Ze wzoru na długość przekątnej kwadratu mamy:
$\mid BD \mid = \mid AB \mid \sqrt2 $
$\mid BD \mid = 4 \sqrt2 $
Długość odcinka $SB$ jest równa połowie długości przekątnej podstawy, zatem
$\mid SB \mid=\frac{\mid BD \mid}{2}=\frac{4 \sqrt2}{2}=2\sqrt2 $
Zauważmy, że trójkąt $SBW$ jest połową kwadratu o boku długości $\mid SB \mid,$ zatem
$\mid SB \mid = \mid SW \mid = 2\sqrt2$
Odcinek $SW$ jest wysokością naszego ostrosłupa, zatem podstawiając do wzoru na objętość otrzymujemy:
$V=\frac{1}{3}\mid AB \mid^2 \cdot \mid SW \mid= \frac{1}{3}4^2 \cdot 2\sqrt2= \frac{32\sqrt2}{3}$
Odpowiedź: Objętość tego ostrosłupa, to $\frac{32\sqrt2}{3}.$

Narysujmy dodatkowo trójkąt $SBW:$
Wiemy, że $\mid AB \mid ^2 =16$
Zatem:
$\mid AB \mid=4 \quad \vee \quad \mid AB \mid=-4$
Odległość musi być nieujemna, zatem
$\mid AB \mid =4$
Ze wzoru na długość przekątnej kwadratu mamy:
$\mid BD \mid = \mid AB \mid \sqrt2 $
$\mid BD \mid = 4 \sqrt2 $
Długość odcinka $SB$ jest równa połowie długości przekątnej podstawy, zatem
$\mid SB \mid=\frac{\mid BD \mid}{2}=\frac{4 \sqrt2}{2}=2\sqrt2 $
Zauważmy, że trójkąt $SBW$ jest połową kwadratu o boku długości $\mid SB \mid,$ zatem
$\mid SB \mid = \mid SW \mid = 2\sqrt2$
Odcinek $SW$ jest wysokością naszego ostrosłupa, zatem podstawiając do wzoru na objętość otrzymujemy:
$V=\frac{1}{3}\mid AB \mid^2 \cdot \mid SW \mid= \frac{1}{3}4^2 \cdot 2\sqrt2= \frac{32\sqrt2}{3}$
Odpowiedź: Objętość tego ostrosłupa, to $\frac{32\sqrt2}{3}.$
5+
