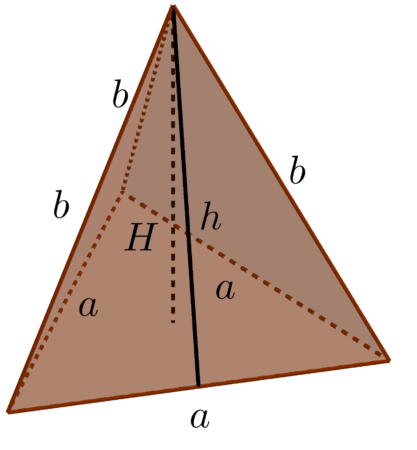
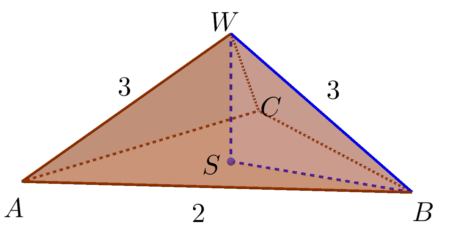
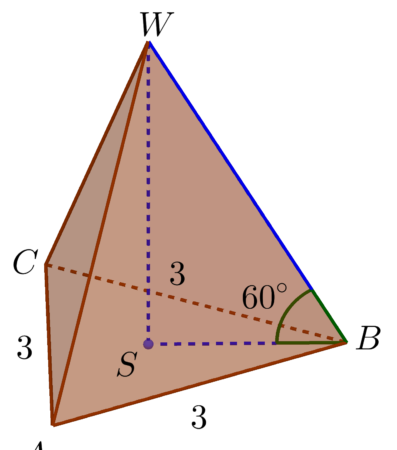
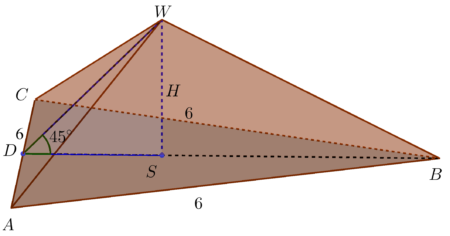
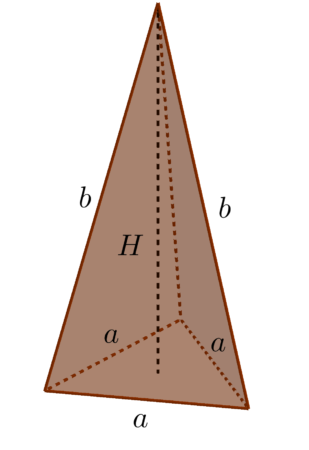
Ostrosłup prawidłowy trójkątny
Tworzenie ostrosłupów jest intuicyjnie nieco trudniejsze od tworzenia graniastosłupów, dlatego poza definicją formalną podamy krótki opis powstawania ostrosłupów krok po kroku.
Ostrosłup prawidłowy trójkątny to ostrosłup, który ma w podstawie trójkąt równoboczny, a jego wysokość pada na punkt przecięcia się wysokości tego trójkąta.
Jak powstaje ostrosłup prawidłowy trójkątny krok po kroku?
- Bierzemy dowolny trójkąt równoboczny i zaznaczamy punkt przecięcia się jego wysokości.
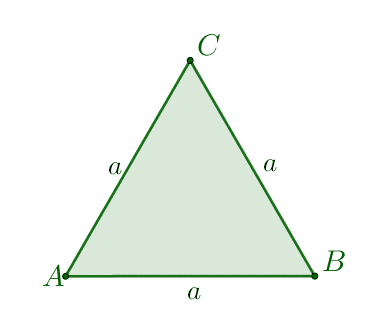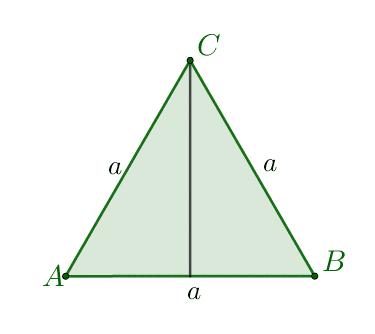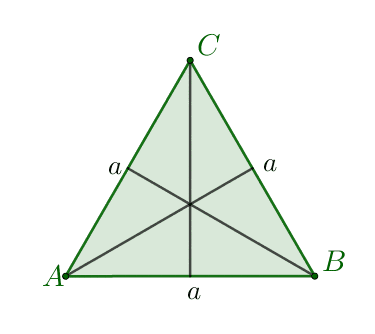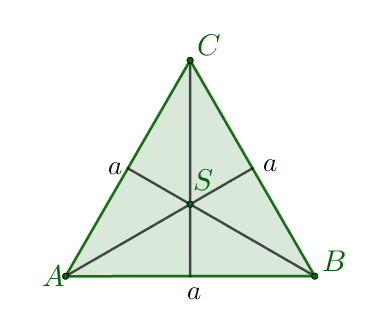
- Na prostej prostopadłej do płaszczyzny naszego trójkąta i przechodzącej przez punkt $S$ wybieramy punkt $W\neq S$. Tworzymy odcinki $AW,\: BW,\: CW$ otrzymana w ten sposób bryła jest ostrosłupem prawidłowym trójkątnym.
Zwróćmy uwagę na to, jak wygląda siatka ostrosłupa prawidłowego trójkątnego i jakie są jej wymiary:
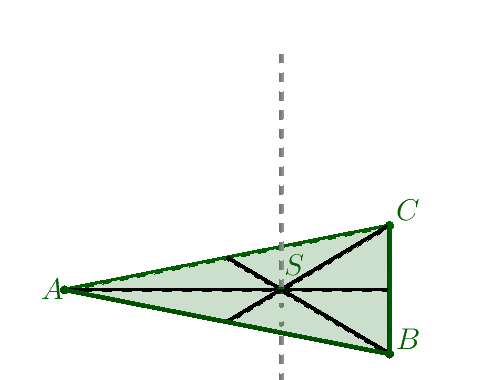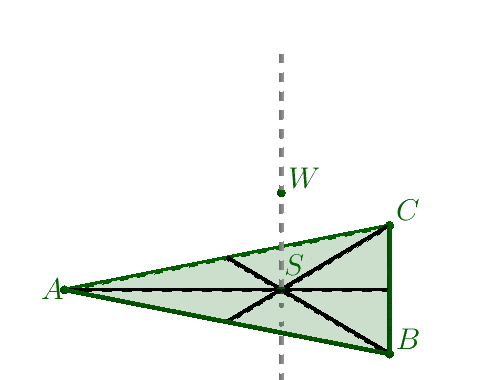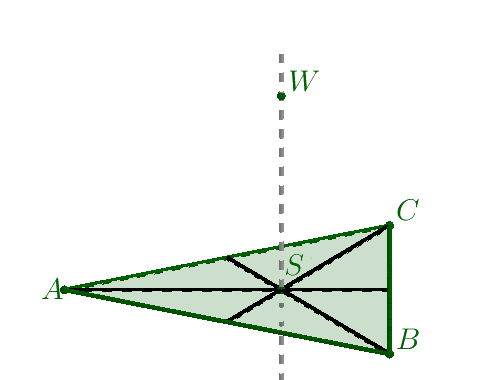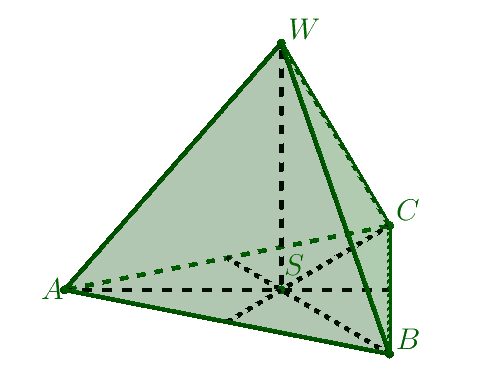
Ostrosłup prawidłowy trójkątny ma zawsze:
- 4 ściany
- 6 krawędzi
- 4 wierzchołki
Objętość ostrosłupa prawidłowego trójkątnego
Objętość ostrosłupa wyraża się wzorem:
$V=\frac{1}{3}Pole\: podstawy\cdot wysokość\: ostrosłupa$
W przypadku ostrosłupa prawidłowego trójkątnego podstawą jest trójkąt równoboczny, zatem
$Pole\: podstawy=\frac{a^2\sqrt3}{4}$
Ostatecznie mamy:
Objętość ostrosłupa prawidłowego trójkątnego wyraża się wzorem:
$$V=\frac{a^2\sqrt3}{12}H$$
$$V=\frac{a^2\sqrt3}{12}H$$
Pole powierzchni całkowitej ostrosłupa prawidłowego trójkątnego
Pole powierzchni całkowitej ostrosłupa prawidłowego trójkątnego można opisać na wiele sposobów w zależności od tego, jakie mamy dostępne dane. Poniżej pokażemy najczęściej zapisywaną formę tego wzoru.
Dla oznaczeń jak na rysunku, pole powierzchni całkowitej ostrosłupa prawidłowego trójkątnego określa wzór:
$$P_{C}=\underbrace{\frac{a^2\sqrt3}{4}}_{Pole\: podstawy}+\overbrace{3}^{3\: ściany\: boczne}\cdot \underbrace{\frac{1}{2}ah}_{Pole\: ściany\: bocznej}=\frac{a^2\sqrt3 + 6ah}{4}$$
