Na początku zdefiniujemy pojęcie potęgi.
$$a^{n} = \underbrace{a\cdot a\cdot a \cdot … \cdot a}_{n-razy}$$
gdzie:
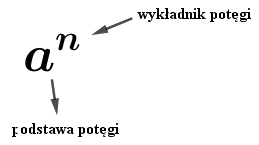
oraz $n$ jest liczbą naturalną większa od 0.
Potęga o wykładniku wymiernym i całkowitym
Teraz podamy wzory na potęgę o wykładniku wymiernym i całkowitym.
$$a^{\color{blue}{-n}} = \frac{1}{a^{\color{blue}{n}}},\;\;\;\;\;a \neq 0, n\in \mathbb{N}$$$${a^{\frac{1}{\color{blue}n}} = \sqrt[\color{blue}n]{a},\;\;\;\;\;a \geq 0, n\in \mathbb{N}}$$ $${{{a^{\frac{\color{red}k}{\color{blue}n}} = (\sqrt[\color{blue}n]{a})^{\color{red}k},\;\;\;\;\;a \geq 0, n\in \mathbb{N},k\in \mathbb{Z_{+}}}}}$$
gdzie:
$\mathbb{Z_{+}}$ – zbiór liczb całkowitych dodatnich.
$$a^{0} = 1$$.
Działania na potęgach
Niech $m,n$ będą dowolnymi liczbami rzeczywistymi.
Jeśli $a > 0$ i $ b > 0$, to zachodzą równości:
$${{a}^{\color{blue}m} \cdot {a}^{\color{red}n} = {a}^{\color{blue}m+\color{red}n}}$$ $${\frac{{a}^{\color{blue}m}}{{a}^{\color{red}n}}={a}^{\color{blue}m-\color{red}n}}$$ $${a}^{\color{red}{n}} \cdot {{b}}^{\color{red}{n}} = \left({{a}}{{b}}\right)^{\color{red}{n}}$$ $$\frac{{a}^{\color{red}{n}}}{{{b}}^{\color{red}{n}}}=\left(\frac{{a}}{{{b}}}\right)^{\color{red}{n}}$$ $$({a}^{\color{blue}m})^{\color{red}n}={a}^{\color{blue}m\cdot \color{red} n}$$ $$({a}^{\color{blue}m})^{\color{red}n}=({a}^{\color{blue}m})^{\color{red}n}=({a}^{\color{red}n})^{\color{blue} m}$$
Przykłady.
$$5^{9} \cdot 5^{17} = 5^{9+17} = 5^{26}$$
$$\left(\frac{1}{2}\right)^{2} \cdot \left(\frac{1}{2}\right)^{3} = \left(\frac{1}{2}\right)^{5}$$
$$\frac{5^{7}}{5^{3}} = 5^{7-3} = 5^{4}$$
$$\frac{\left(\frac{1}{2}\right)^{10}}{\left(\frac{1}{2}\right)^{4}} = \left(\frac{1}{2}\right)^{10-4}=\left(\frac{1}{2}\right)^{6}=\frac{1^{6}}{2^{6}}=\frac{1}{2^{6}}$$
$$\frac{10^{100}}{10^{300}} = 10^{100-300} = 10^{-200} = \left(\frac{1}{10}\right)^{200}$$
$$5^{7}\cdot 6^{7}= (5\cdot 6)^{7} = 30^{7}$$
$$\left(\frac{1}{2}\right)^{100} \cdot 8^{100}= \left(\frac{1}{2}\cdot 8\right)^{100} = 4^{100}$$
$$(6^{11})^{5} = 6^{11\cdot5}=6^{55}$$
$$(3^{\frac{1}{2}})^{8} = 3^{\frac{1}{2}\cdot8} = 3^{4}$$
$$(2^{\sqrt{2}})^{\sqrt{5}} = 2^{\sqrt{2}\cdot\sqrt{5}} = 2^{\sqrt{10}}$$

Matura z matematyki?
Oferujemy SuperKorepetycje - korki online połączone z przejrzyście zrozumiałymi filmikami do nauki własnej
Zobacz więcejZadania
Oblicz wartość wyrażenia $\left(\frac{2^{6}}{2^{3}}\right)^{3}$
Zatem:
gdzie:
$1$ – pierwszy wzór zadania 1,
$2$ – drugi wzór zadania 1.
Zapisz liczbę w postaci potęgi 2 liczbę: $\sqrt{8}\cdot \sqrt{16}$.
Zatem:
$1$ – pierwszy wzór zadania 2,
$2$ – drugi wzór zadania 2.
Oblicz $\frac{81^{2}\cdot16^{3}\cdot12}{8^{3}\cdot27^{3}\cdot72}$
Zamieńmy liczby w ułamek na potęgi o podstawie 2 i 3 oraz rozłóżmy liczby 12 i 72 na czynniki pierwsze, tzn.:
Ustaw liczby w kolejności rosnącej:
- $-2^{4},~\left(-\frac{1}{2}\right)^{5},~(-2)^{5}$
- $\left(\frac{1}{2}\right)^{2},~\left(\frac{1}{2}\right)^{6},~\left(\frac{1}{2}\right)^{3}$
Mamy zatem:
Wobec tego mamy: $$(-2)^{5}~<~-2^{4}~<~\left(-\frac{1}{2}\right)^{5}$$ W następnym przykładzie zamieńmy najpierw ułamki na liczby, korzystając ze wzoru $a^{-n} = \frac{1}{a^{n}}$, czyli:
porządkując potęgi o takich samych podstawach będziemy kierowali się wykładnikiem potęgi. Im większy wykładnik – tym większa liczba. U nas wykładniki to $-2, -6~$ i $-3$, zatem w kolejności od najmniejszej do największej: $$2^{-6}~<~2^{-3}~<~2^{-2}.$$
Oblicz wartość wyrażenia:
- $(-2)^{4}+(1\frac{1}{3})^{2} – 3^{0}$
- $-3^{4} + (-3)^{2} – (2\frac{1}{2})^{3}$
Zatem:$$(-2)^{4}+\left(1\frac{1}{3}\right)^{2} – 3^{0} = 16 + \left(\frac{4}{3}\right)^{2}-1 = 16+\frac{16}{9}-1 =$$$$=\frac{144}{9}+\frac{16}{9}-\frac{9}{9}=\frac{144+16-9}{9}=\frac{151}{9}=16\frac{7}{9}$$
$$-3^{4} + (-3)^{2} – \left(2\frac{1}{2}\right)^{3}=-81+9-\left(\frac{5}{2}\right)^{3} = -72-\frac{125}{8} =$$$$= -\frac{576}{8} – \frac{125}{8} = \frac{-576-125}{8} = \frac{-701}{8} = 87\frac{5}{8}$$
