Czym jest proporcja?

Proporcją nazywamy równość dwóch ilorazów, co zapisujemy w postaci
$$\Large{\frac ab=\frac cd}$$
gdzie $b\neq0\;$ i $d\neq0\;$ (Nie dzielimy przez 0!).

Bardzo często styczność z proporcjami mamy w zadaniach związanych z obliczaniem procentów.

Do wyznaczenia naszej niewiadomej jedną z najbardziej przystępnych metod jest metoda “na krzyż”. Po ułożeniu odpowiedniej proporcji mnożymy wielkości po przekątnej i przyrównujemy je do siebie.

Uwaga: Najważniejsze jest ułożenie dobrej proporcji, dlatego należy pamiętać, że w słupku procenty są zawsze pod procentami, liczby po liczbami.
Przykład: Oblicz $25\%$ z liczby $20$.
Układamy proporcję:

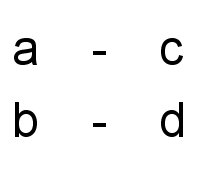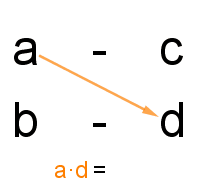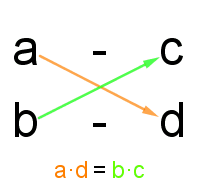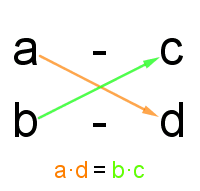
$\textcolor{red}{20}$ $-$ $\textcolor{blue}{100\%}$
$\textcolor{blue}{x}$ $-$ $\textcolor{red}{25\%}$		 liczba $20$ odpowiada $100\%$
$x$ jest szukaną liczbą odpowiadającą $25\%$ z liczby $20$

Teraz wymnażamy “na krzyż”:
$\textcolor{red}{20\cdot25\%}=\textcolor{blue}{100\%\cdot x}$
Zatem
$x=\frac{20\cdot25\%}{100\%}=5$

Odpowiedź: Liczbą, która stanowi $25\%$ liczby $20$ jest liczba $5$.

Uwaga: Analogicznie wykonując tę operację można zapamiętać, że liczbę znajdującą się po przekątnej niewiadomej od razu zapisujemy w mianowniku ułamka, a iloczyn pozostałych liczb w liczniku.
Przykład: Oblicz $5\%$ z liczby $70$.
Najpierw układamy proporcję:
$\textcolor{red}{70}$ $-$ $\textcolor{blue}{100\%}$
$\textcolor{blue}{x}$ $-$ $\textcolor{red}{5\%}$
 
Wymnażamy „na krzyż”:
$\textcolor{red}{70\cdot 5\%}=\textcolor{blue}{100\% \cdot x}$
Zatem
$x=\frac{70\cdot5\%}{100\%}=3,5$

Odpowiedź: Liczbą, która stanowi $5\%$ liczby $70$ jest liczba $3,5$.
Przykład: Oblicz, jakim procentem liczby $48$ jest liczba $4$.
Układamy proporcję:

$\textcolor{blue}{48}$ $-$ $\textcolor{red}{100\%}$
$\textcolor{red}{4}$ $-$ $x$		 liczba $48$ odpowiada $100\%$
$x$ jest szukanym procentem jaki stanowi liczba $4$ z liczby $48$

Wymnażamy „na krzyż”:
$48\cdot x=100\%\cdot 4$
Zatem
$x=\frac{4\cdot100\%}{48}=8\frac13\%$

Odpowiedź: Liczba $4$ stanowi $8\frac{1}{3}\%$ liczby $48$.

Przykład: Znajdź liczbę, której $165\%$ wynosi $495$.
Układamy proporcję:

$\textcolor{blue}{165\%}$ $-$ $\textcolor{red}{495}$
$\textcolor{red}{100\%}$ $-$ $x$		 liczba $495$ odpowiada $165\%$
$x$ jest szukaną liczbą, która odpowiada $100\%$

Następnie wymnażamy „na krzyż”:
$165\%\cdot x=495\cdot 100\%$
$x=\frac{495\cdot100\%}{165\%}=300$

Odpowiedź: Liczbą, której $165\%$ wynosi $495$ jest liczba $300$.

Więcej przykładów

Przykład: W sklepie obowiązuje $15\%$ obniżka cen. Oblicz cenę kurtki, która przed obniżką kosztowała $120$ zł.
Ceny obniżono o $15\%$. Zatem
$100\%-15\%=85\%$
 
Szukamy liczby odpowiadającej $85\%$ z liczby $120$.
Układamy następującą proporcję:
$\textcolor{blue}{100\%}$ — $\textcolor{red}{120}$
$\textcolor{red}{85\%}$ — $x$
 
Wymnażamy „na krzyż”:
$100\%\cdot x=120\cdot 85\%$
$x=\frac{120\cdot85\%}{100\%}=102$

Odpowiedź: Po obniżce kurtka kosztuje $102$ zł.
Przykład: Cena bluzki wynosiła $68$ zł. W ciągu roku cena ta została obniżona dwukrotnie: najpierw o $10\%$, a następnie o $20\%$. Ile kosztuje bluzka po obu obniżkach?
Krok 1: Najpierw cena bluzki została obniżona o $10\%$. Zatem
$100\%-10\%=90\%$
$ $
Szukamy $90\%$ z liczby $68$:
$\textcolor{blue}{100\%}$ $-$ $\textcolor{red}{68}$
$\textcolor{red}{90\%}$ $-$ $x$
 
Mnożymy „na krzyż”:
$100\%\cdot x=68\cdot 90\%$
Otrzymujemy, że
$x=\frac{68\cdot90\%}{100\%} = 61,20$

Krok 2: Nowo obliczona cena staje się naszą 100% wartością, od której odejmujemy jeszcze 20% wartości (druga obniżka cen):
$100\%-20\%=80\%%$
 
Zatem końcowa cena będzie odpowiadała $80\%$ ceny po pierwszej obniżce, czyli $61,20$. Otrzymujemy następującą proporcję:
$\textcolor{blue}{100\%}$ $-$ $\textcolor{red}{61,20}$
$\textcolor{red}{80\%}$ $-$ $x$
$100\%\cdot x=61,20\cdot 80\%$
 
Mamy, że
$x=\frac{61,20\cdot80\%}{100\%} = 48,96$

Odpowiedź: Cena bluzki po obu obniżkach wynosi $48,96$ zł.
Przykład: Liczba osobników pewnego zagrożonego wyginięciem gatunku zwierząt wzrosła w stosunku do liczby tych zwierząt z 31 grudnia 2011 r. o $120\%$ i obecnie jest równa $8910$. Ile zwierząt liczyła populacja tego gatunku w ostatnim dniu 2011 roku?
Skoro liczba populacji wzrosła o $120\%$ to do $100\%$ liczby zwierząt z 2011 roku dodajemy $120\%$. Zatem
$100\%+120\%=220\%$
 
Układamy proporcję, w której $220\%$ odpowiada liczbie $8910$, zaś $x$ to niewiadoma odpowiadająca $100\%$ obecnej populacji:
$\textcolor{blue}{220\%}$ $—$ $\textcolor{red}{8910}$
$\textcolor{red}{100\%}$ $—$ $x$
$220\%\cdot x=8910\cdot 100\%$
$x=\frac{8910\cdot100\%}{220\%}=4050$

Odpowiedź: W ostatnim dniu 2011 roku populacja liczyła 4050 zwierząt.
12+
Klaudia Mularczyk