Zanim opiszemy jak wyznaczyć równanie prostej prostopadłej do danej prostej lub sprawdzimy czy dane dwie proste są prostopadłe, przypomnijmy sobie niezbędne informacje.

Każda prosta posiada równanie kierunkowe postaci:
$$\Large{y=ax+b}$$
gdzie $a$ to współczynnik kierunkowy.

Kiedy dwie dane proste są prostopadłe?

Rozwiązując zadania tego typu mamy do dyspozycji dwie metody.

Metoda 1

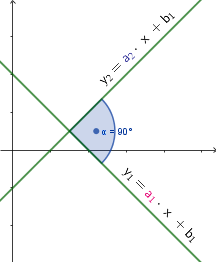
Dwie proste:

$$\Large{y_1={\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1}x+b_1\hspace{1,5cm} y_2={\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2}x+b_2}$$

są prostopadłe, gdy
$$\Large{\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1\cdot\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2}{\textcolor{black}=-1}$$
Lub prościej:
$$\Large{\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1{\textcolor{black}=}{\textcolor{black}-}\frac{\textcolor{black}1}{\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2}}$$
czyli $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$ jest odwrotny i przeciwny do $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$.

Przykład: Prosta o równaniu $y=mx+1$ jest prostopadła do prostej o równaniu $y=-\frac52x+2$. Wyznacz $m$.
Jeżeli dwie proste są prostopadłe, to za pomocą jednego współczynnika kierunkowego $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$
jesteśmy w stanie wyznaczyć $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$.

Z polecenia możemy wywnioskować, że

dla $y=-\frac52x+2$ $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$=${\color[rgb]{0.9, 0.0, 0.45}-\frac52}$

dla $y=mx+1$ $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$=${\color[rgb]{0.2, 0.2, 0.6}m}$.

Z własności $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$=$-\frac1{\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2}$ mamy, że

${\color[rgb]{0.9, 0.0, 0.45}-\frac52}=-\frac1{\color[rgb]{0.2, 0.2, 0.6}m}$ $|$ $\cdot $$m$
$-\frac52$ $\cdot$$m$=$-1$ $|:(-\frac52)$
$m=\frac25$

Odpowiedź: $m=\frac25$.

Uwaga: Dla $a_1=-\frac52$ czymś przeciwnym jest $\frac52$ a odwrotnym do tego jest $\frac25$. To analogiczny sposób wyznaczenia $m$.

Przykład: Które z podanych prostych są prostopadłe?

A. $y=2x+4$ $y=\frac12x+5$
B. $y=2x+2$ $y=2x-2$
C. $y=2x$ $y=-2x-1$
D. $y=2x-2$ $y=-\frac12x-4$
Aby zrozumieć ideę prostych prostopadłych przeanalizujemy przykład krok po kroku.
A. $y={\color[rgb]{0.9, 0.0, 0.45}2}x+4$ $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$=${\color[rgb]{0.9, 0.0, 0.45}2}$ $y={\color[rgb]{0.2, 0.2, 0.6}\frac12}x+5$ $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$=${\color[rgb]{0.2, 0.2, 0.6}\frac12}$ ${\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1}\cdot{\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2}\neq-1$
B. $y={\color[rgb]{0.9, 0.0, 0.45}2}x+2$ $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$=${\color[rgb]{0.9, 0.0, 0.45}2}$ $y={\color[rgb]{0.2, 0.2, 0.6}2}x-2$ $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$=${\color[rgb]{0.2, 0.2, 0.6}2}$ ${\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1}\cdot{\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2}\neq-1$
C. $y={\color[rgb]{0.9, 0.0, 0.45}2}x$ $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$=${\color[rgb]{0.9, 0.0, 0.45}2}$ $y={\color[rgb]{0.2, 0.2, 0.6}-2}x-1$ $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$=${\color[rgb]{0.2, 0.2, 0.6}-2}$ ${\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1}\cdot{\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2}\neq-1$
D. $y={\color[rgb]{0.9, 0.0, 0.45}2}x-2$ $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$=${\color[rgb]{0.9, 0.0, 0.45}2}$ $y={\color[rgb]{0.2, 0.2, 0.6}-\frac12}x-4$ $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$=${\color[rgb]{0.2, 0.2, 0.6}-\frac12}$ ${\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1}\cdot{\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2}=-1$

Proste w przykładzie D. są prostopadłe, ponieważ spełniają podany warunek.
Spójrz! Dla $a_1=2$ czymś odwrotnym jest $\frac12$ a czymś przeciwnym do $\frac12$ jest $-\frac12$ czyli nasze $a_2$.

Przykład: Proste opisane równaniami $y=\frac2{m-1}x+m-1$ oraz $y=mx+\sqrt{\frac1{m+7}}$ są prostopadłe, gdy

A. $m=2$

 B. $m=\frac12$ C. $m=\frac13$ D. $m=-2$
Do sprawdzania czy proste są prostopadłe potrzebujemy tylko współczynników kierunkowych
czyli tego co znajduje się przy $x$.
Przeanalizujmy:
$y$=$\color[rgb]{0.9, 0.0, 0.45}\frac2{m-1}$$x+m-1$ $y={\color[rgb]{0.2, 0.2, 0.6}m}x+\sqrt{\frac1{m+7}}$
Wiemy już, że
$\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$=$\color[rgb]{0.9, 0.0, 0.45}\frac2{m-1}$ $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$=${\color[rgb]{0.2, 0.2, 0.6}m}$

Podstawmy do wzoru który gwarantuje prostopadłość prostych:

$\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1\cdot\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2=-1$
$\color[rgb]{0.9, 0.0, 0.45}\frac2{m-1}$$\cdot$${\color[rgb]{0.2, 0.2, 0.6}m}$=$-1$
$\frac{2m}{m-1}$=$-1$ $|\cdot(m-1)$
 

$2m=-1\cdot(m-1)$
$2m=-(m-1)$
$2m=-m+1$ $|+m$
$3m=1$ $|:3$
$m$=$\frac13$

Odpowiedź: C.

Metoda 2

Dwie proste o równaniach ogólnych:

$$\Large{A_{1}x+B_{1}y+C_{1}=0 \hspace{1,5cm}A_{2}x+B_{2}y+C_{2}=0}$$

są prostopadłe, gdy
$$\Large{A_{1}A_{2}+B_{1}B_{2}=0}$$

Uwaga: Tego nie musisz wkuwać! Wybrane wzory matematyczne – CKE strona 5.
Przykład: Zbadaj, czy proste $5x-y+5=0$ i $-\frac15x-y+7=0$ są prostopadłe.
Korzystając z powyższej metody mamy, że:
$A_1+B_1+C_1=0$ $A_2+B_2+C_2=0$
$5x-y+5=0$ $-\frac15x-y+7=0$
${\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}A}_1}$=${\color[rgb]{0.0, 0.0, 0.5}5}$ $\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}B}_1$=${\color[rgb]{0.0, 0.5, 0.5}-1}$ $\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}A}_2$=${\color[rgb]{0.0, 0.5, 0.0}-\frac15}$ $\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}B}_2$=${\color[rgb]{0.51, 0.5, 0.0}-1}$
 

Musimy sprawdzić, czy ${\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}A}_1}$ $\cdot$ $\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}A}_2$ + $\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}B}_1$ $\cdot$ $\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}B}_2$ $=0$
Podstawmy $\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}A}_1$, $\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}A}_2$, $\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}B}_1$, $\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}B}_2$
${\color[rgb]{0.0, 0.0, 0.5}5}$ $\cdot$ ${\color[rgb]{0.0, 0.5, 0.0}-\frac15}$ + ${\color[rgb]{0.0, 0.5, 0.5}(-1)}$ $\cdot$ ${\color[rgb]{0.51, 0.5, 0.0}(-1)}$ = $-1+1$ = $0$

Odpowiedź: Zatem proste są prostopadłe.

Przykład: Zbadaj, czy proste $-2x-y+2$ i $-\frac12c-y+3=0$ są prostopadłe.
Korzystając z powyższej metody mamy, że:
$A_1+B_1+C_1=0$ $A_2+B_2+C_2=0$
$-2x-y+2=0$ $-\frac12x-y+3=0$
${\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}A}_1}$=${\color[rgb]{0.0, 0.0, 0.5}-2}$ $\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}B}_1$=${\color[rgb]{0.0, 0.5, 0.5}-}{\color[rgb]{0.0, 0.5, 0.5}1}$ $\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}A}_2$=${\color[rgb]{0.0, 0.5, 0.0}-\frac12}$ $\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}B}_2$=${\color[rgb]{0.51, 0.5, 0.0}-1}$
 

Musimy sprawdzić, czy ${\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}A}_1}$ $\cdot$ $\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}A}_2$ + $\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}B}_1$ $\cdot$ $\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}B}_2$ $=0$
Podstawmy $\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}A}_1$, $\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}A}_2$, $\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}B}_1$, $\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}B}_2$
${\color[rgb]{0.0, 0.0, 0.5}-2}$ $\cdot$ ${\color[rgb]{0.0, 0.5, 0.0}-\frac12}$ + ${\color[rgb]{0.0, 0.5, 0.5}(-1)}$ $\cdot$ ${\color[rgb]{0.51, 0.5, 0.0}(-1)}$ = $1+1$ = $2\neq0$

Odpowiedź: Zatem proste nie są prostopadłe.

Wyznaczanie prostej prostopadłej do danej prostej przechodzącej przez punkt

Przykład: Wyznacz równanie prostej $k$ prostopadłej do prostej $l:$ $y=x$ przechodzącej przez punkt $A=(2,1)$.
Równanie kierunkowe prostej dane jest wzorem $y=ax+b$.
Skoro proste $y=x$ i $y=ax+b$ są prostopadłe, to $a=-1$. Wiemy więc, że $k:$ $y=-x$+${\color[rgb]{0.5, 0.25, 0.0}b}$.
Aby wyznaczyć ${\color[rgb]{0.5, 0.25, 0.0}b}$ musimy skorzystać z tego, że prosta przechodzi przez punkt $A=({\color[rgb]{0.0, 0.8, 0.27}2},{\color[rgb]{1.0, 0.4, 0.0}1})$. Podstawmy punkt $A$ do prostej $k$, czyli przepiszmy ${\color[rgb]{0.0, 0.8, 0.27}x}={\color[rgb]{0.0, 0.8, 0.27}2}$ i ${\color[rgb]{1.0, 0.4, 0.0}y}={\color[rgb]{1.0, 0.4, 0.0}1}$ w odpowiednie miejsca równania prostej $k:$ ${\color[rgb]{1.0, 0.4, 0.0}y}=-{\color[rgb]{0.0, 0.8, 0.27}x}+{\color[rgb]{0.5, 0.25, 0.0}b}$. Mamy więc, że
${\color[rgb]{1.0, 0.4, 0.0}1}=$$-{\color[rgb]{0.0, 0.8, 0.27}2}$+${\color[rgb]{0.5, 0.25, 0.0}b}$
${\color[rgb]{0.5, 0.25, 0.0}b}=1+2$
${\color[rgb]{0.5, 0.25, 0.0}b}=3$
Zatem $k:$ $y=-x+{\color[rgb]{0.5, 0.25, 0.0}3}$.
Odpowiedź: $k:$ $y=-x+3$.

 

 

0
Anita Księżak