Zanim opiszemy jak wyznaczyć równanie prostej równoległej do danej prostej lub sprawdzimy,
czy dane dwie proste są równoległe, przypomnijmy sobie niezbędne informacje.

Każda prosta posiada równanie kierunkowe postaci:
$$\Large{y=ax+b}$$
gdzie $a$ to współczynnik kierunkowy.

Kiedy dwie dane proste są równoległe?

Rozwiązując zadania tego typu mamy do dyspozycji dwie metody.

Metoda 1

Dwie proste:

$$\Large{y_1={\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1}x+b_1\hspace{1,5cm} y_2={\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2}x+b_2}$$

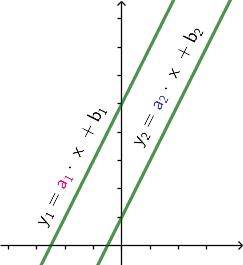
są równoległe, gdy ich współczynniki kierunkowe są równe, czyli
$$\Large{\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1=\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2}$$
Lub prościej: to co stoi przy $x$ jest takie samo.

Przykład: Które z podanych prostych są równoległe?

A $y=\frac13x+7$ $y=-\frac13x+7$
B $y=\frac28x+6$ $y=-\frac82x+9$
C $y=x+2$ $y=x+7$
D $y=7x+2$ $y=12x+7$
Aby rozwiązać to zadanie przeanalizujmy współrzędne kierunkowe poszczególnych równań. Następnie sprawdźmy, czy to co stoi przy $x$ jest takie samo.
A $y={\color[rgb]{0.9, 0.0, 0.45}\frac13}x+7$ $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$=${\color[rgb]{0.9, 0.0, 0.45}\frac13}$ $y={\color[rgb]{0.2, 0.2, 0.6}-\frac13}x+7$ $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$=${\color[rgb]{0.2, 0.2, 0.6}-\frac13}$ $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$ $\neq$ $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$
B $y={\color[rgb]{0.9, 0.0, 0.45}\frac28}x+6$ $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$=${\color[rgb]{0.9, 0.0, 0.45}\frac28}$ $y={\color[rgb]{0.2, 0.2, 0.6}-\frac82}x+9$ $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$=${\color[rgb]{0.2, 0.2, 0.6}-\frac82}$ $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$ $\neq$ $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$
C $y={\color[rgb]{0.9, 0.0, 0.45}1}x+2$ $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$=${\color[rgb]{0.9, 0.0, 0.45}1}$ $y={\color[rgb]{0.2, 0.2, 0.6}1}x+7$ $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$=${\color[rgb]{0.2, 0.2, 0.6}1}$ $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$ = $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$
D $y={\color[rgb]{0.9, 0.0, 0.45}7}x+2$ $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$=${\color[rgb]{0.9, 0.0, 0.45}7}$ $y={\color[rgb]{0.2, 0.2, 0.6}12}x+7$ $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$=${\color[rgb]{0.2, 0.2, 0.6}12}$ $\color[rgb]{0.9, 0.0, 0.45}{\color[rgb]{0.9, 0.0, 0.45}a}_1$ $\neq$ $\color[rgb]{0.2, 0.2, 0.6}{\color[rgb]{0.2, 0.2, 0.6}a}_2$

Odpowiedź: C.

Przykład: Ile wynosi współczynnik kierunkowy prostej równoległej do prostej $y=2x+1$?
Gdy $y=2x+1$ to $a_1=2$. Wynika z tego, że współczynnik kierunkowy prostej równoległej do niej wynosi $a_2=a_1$, czyli $a_2=2$.
$ $
Odpowiedź: Współczynnik kierunkowy prostej równoległej wynosi $a_2=2$.
Przykład: Prosta $k$ o równaniu $y=\frac12x+3$ jest równoległa do prostej $l$ o równaniu $y=(6-m)x+5$. Wyznacz $m$.
Jeśli proste $k$ i $l$ są równoległe, to ich współczynniki kierunkowe są równe.
Wiemy, że $a_1=\frac12$.
$ $
Skoro $a_1=6-m$, to mamy:
$\frac12-6=-m$
$-5\frac12=-m$
$m=5\frac12$
$ $
Odpowiedź: $m=5\frac12$.

Metoda 2

Dwie proste o równaniach ogólnych:

$$\Large{A_{1}x+B_{1}y+C_{1}=0 \hspace{1,5cm}A_{2}x+B_{2}y+C_{2}=0}$$

są równoległe, gdy
$$\Large{A_{1}B_{2}-A_{2}B_{1}=0}$$

Uwaga: Tego nie musisz wkuwać! Wybrane wzory matematyczne – CKE strona 5.
Przykład: Zbadaj, czy proste $x-y+2=0$ i $x-y+7=0$ są równoległe.
Korzystając z powyższej metody mamy, że:
$A_1x+B_1y+C_1=0$ $A_2x+B_2y+C_2=0$
$x-y+2=0$ $x-y+7=0$
${\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}A}_1}={\color[rgb]{0.0, 0.0, 0.5}1}$ $\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}B}_1={\color[rgb]{0.0, 0.5, 0.5}-}{\color[rgb]{0.0, 0.5, 0.5}1}$ $\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}A}_2={\color[rgb]{0.0, 0.5, 0.0}1}$ $\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}B}_2={\color[rgb]{0.51, 0.5, 0.0}1}$
 

Musimy sprawdzić, czy ${\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}A}_1}$ $\cdot$ $\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}B}_2$ $-$ $\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}A}_2$ $\cdot$ $\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}B}_1$ $=0$
Podstawmy $\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}A}_1$, $\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}A}_2$, $\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}B}_1$, $\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}B}_2$
${\color[rgb]{0.0, 0.0, 0.5}1}\cdot{\color[rgb]{0.0, 0.5, 0.5}-}{\color[rgb]{0.0, 0.5, 0.5}1}-{\color[rgb]{0.0, 0.5, 0.0}1}\cdot{\color[rgb]{0.51, 0.5, 0.0}1}=-1-(-1)=-1+1=0$

Odpowiedź: Proste są równoległe.

Przykład: Zbadaj, czy proste $2x+12y-3=0$ i $8x-12y-7=0$ są równoległe.
Korzystając z powyższej metody mamy, że:
$A_1x+B_1y+C_1=0$ $A_2x+B_2y+C_2=0$
$2x+12y-3=0$ $8x-12y-7=0$
${\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}A}_1}$=${\color[rgb]{0.0, 0.0, 0.5}2}$ ${\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}B}_1}$=${\color[rgb]{0.0, 0.5, 0.5}12}$ $\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}A}_2$=${\color[rgb]{0.0, 0.5, 0.0}8}$ $\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}B}_2$=${\color[rgb]{0.51, 0.5, 0.0}12}$
 

Musimy sprawdzić, czy ${\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}A}_1}$ $\cdot$ $\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}B}_2$ $-$ $\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}A}_2$ $\cdot$ $\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}B}_1$ $=0$
Podstawmy $\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}A}_1$, $\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}A}_2$, $\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}B}_1$, $\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}B}_2$
${\color[rgb]{0.0, 0.0, 0.5}2}$ $\cdot$ ${\color[rgb]{0.0, 0.5, 0.5}12}$ – ${\color[rgb]{0.0, 0.5, 0.0}8}$ $\cdot$ ${\color[rgb]{0.51, 0.5, 0.0}12}$ $=$ $-72$ $\neq$ $0$

Odpowiedź: Proste $2x+12y-3=0$ i $8x-12y-7=0$ nie są równoległe.

Wyznaczanie prostej równoległej do danej prostej przechodzącej przez punkt

Przykład: Wyznacz równanie prostej $k$ równoległej do prostej $l:$ $y=2x+6$ przechodzącej przez punkt $A=(1,3)$.
Równanie kierunkowe prostej dane jest wzorem $y=ax+b$.
Skoro proste $y=2x+6$ i $y=ax+b$ są równoległe, to $a=2$.
Wiemy więc, że $k:$ $y=2x+{\color[rgb]{0.5, 0.25, 0.0}b}$.
$ $
Aby wyznaczyć ${\color[rgb]{0.5, 0.25, 0.0}b}$ musimy skorzystać z tego, że prosta przechodzi przez punkt $A=({\color[rgb]{0.0, 0.8, 0.27}1},{\color[rgb]{1.0, 0.4, 0.0}3})$.
Podstawmy punkt $A$ do prostej $k$, czyli przepiszmy ${\color[rgb]{0.0, 0.8, 0.27}x}={\color[rgb]{0.0, 0.8, 0.27}1}$ i ${\color[rgb]{1.0, 0.4, 0.0}y}={\color[rgb]{1.0, 0.4, 0.0}3}$ w odpowiednie miejsca równania prostej $k:$ ${\color[rgb]{1.0, 0.4, 0.0}y}=2{\color[rgb]{0.0, 0.8, 0.27}x}+{\color[rgb]{0.5, 0.25, 0.0}b}$.
$ $
Mamy więc, że
${\color[rgb]{1.0, 0.4, 0.0}3}=2\cdot{\color[rgb]{0.0, 0.8, 0.27}1}+{\color[rgb]{0.5, 0.25, 0.0}b}$
$3=2+{\color[rgb]{0.5, 0.25, 0.0}b}$
${\color[rgb]{0.5, 0.25, 0.0}b}=1$
Zatem $y=2x+{\color[rgb]{0.5, 0.25, 0.0}1}$.
$ $
Odpowiedź: $k:$ $y=2x+1$.
Przykład: Wyznacz równanie prostej $k$ równoległej do prostej $l:$ $y=2x+6$ przechodzącej przez początek układu współrzędnych.
Wiemy, że szukana prosta $k:$ $y=ax+b$ przechodzi przez początek układu współrzędnych, czyli $B=(0,0)$.
Z faktu, że jest ona równoległa do $l:$ $y=2x+6$ mamy, że $k:$ $y=2x+b$.

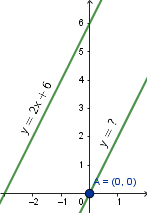
W celu wyznaczenia ${\color[rgb]{0.5, 0.25, 0.0}b}$ podstawmy punkt $B$ do prostej $k$, czyli przepiszmy ${\color[rgb]{0.0, 0.8, 0.27}x}={\color[rgb]{0.0, 0.8, 0.27}0}$ i ${\color[rgb]{1.0, 0.4, 0.0}y}={\color[rgb]{1.0, 0.4, 0.0}0}$
w odpowiednie miejsca równania prostej $k:$ ${\color[rgb]{1.0, 0.4, 0.0}y}=2{\color[rgb]{0.0, 0.8, 0.27}x}+{\color[rgb]{0.5, 0.25, 0.0}b}$.
$ $
Mamy więc, że
${\color[rgb]{1.0, 0.4, 0.0}0}=2$ $\cdot$ ${\color[rgb]{0.0, 0.8, 0.27}0}+{\color[rgb]{0.5, 0.25, 0.0}b}$
${\color[rgb]{0.5, 0.25, 0.0}b}=0$
Zatem $y=2x+{\color[rgb]{0.5, 0.25, 0.0}0}$.
$ $
Odpowiedź: $k:$ $y=2x$.
1+
Anita Księżak