Kąt
Zanim omówimy rodzaje kątów, zdefiniujmy pojęcie kąta.
Kąt to figura geometryczna składająca się z dwóch półprostych o wspólnym początku oraz z obszaru płaszczyzny wyznaczonego przez te półproste.
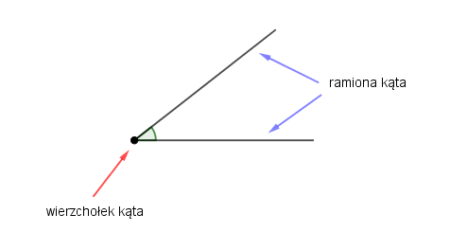
Uwaga: Najczęściej stosowaną miarą kąta jest miara stopniowa.
Rodzaje kątów
- Kąt zerowy ma miarę $0^\circ$.

- Kąt ostry to kąt, którego miara stopniowa należy do przedziału $(0^\circ,90^\circ)$ .

- Kąt prosty ma miarę $90^\circ$.

Uwaga: Kąt prosty zaznaczamy kropką.
- Kąt rozwarty to kąt, którego miara stopniowa należy do przedziału $(90^\circ,180^\circ)$.

- Kąt półpełny ma miarę $180^\circ$.

- Kąt pełny ma miarę $360^\circ$.

- Kąt wypukły to kąt, którego miara stopniowa należy do $<0^\circ,180^\circ>\hspace{0,10cm}\cup\hspace{0,10cm}\{360^\circ\}$.
- Kąt wklęsły to kąt, którego miara stopniowa należy do przedziału $(180^\circ,360^\circ)$.
Przykład: Przez wierzchołek rozwartego kąta ABC poprowadzono dwie proste prostopadłe do ramion kąta. Proste te przecinają się pod kątem $40^\circ$. Oblicz miarę kąta ABC.
Rozwiązanie:
Mamy kąt rozwarty ABC:

Poprowadzimy teraz proste prostopadłe do ramion kąt ABC:
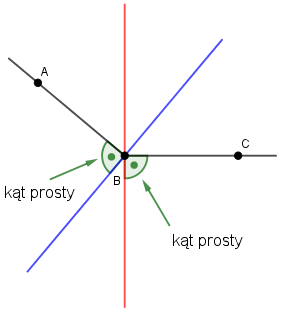
Z treści zadania wiemy, że proste prostopadłe przecinają się pod kątem $40^\circ$.
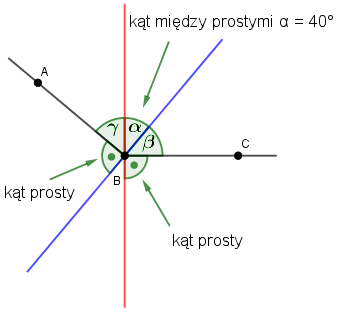
Zatem kąt $\beta=90^\circ-\alpha=90^\circ-40^\circ=50^\circ$.
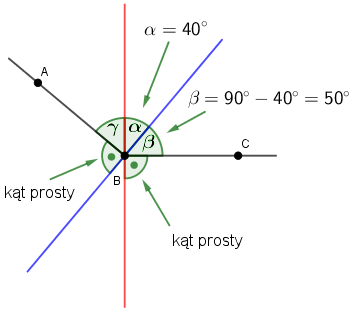
Analogicznie obliczamy kąt $\gamma=90^\circ-\alpha=90^\circ-40^\circ=50^\circ$.
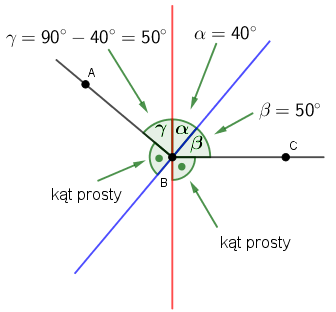
Zatem miara kąta ABC wynosi:
$|\measuredangle{ABC}|=\alpha+\beta+\gamma=40^\circ+50^\circ+50^\circ=140^\circ$.
Odpowiedź: Miara kąta ABC wynosi $140^\circ$.
Mamy kąt rozwarty ABC:

Poprowadzimy teraz proste prostopadłe do ramion kąt ABC:

Z treści zadania wiemy, że proste prostopadłe przecinają się pod kątem $40^\circ$.

Zatem kąt $\beta=90^\circ-\alpha=90^\circ-40^\circ=50^\circ$.

Analogicznie obliczamy kąt $\gamma=90^\circ-\alpha=90^\circ-40^\circ=50^\circ$.

Zatem miara kąta ABC wynosi:
$|\measuredangle{ABC}|=\alpha+\beta+\gamma=40^\circ+50^\circ+50^\circ=140^\circ$.
Odpowiedź: Miara kąta ABC wynosi $140^\circ$.
Dwusieczna kąta
Dwusieczna kąta to półprosta dzieląca go na dwa równe kąty.

16+
