Miara łukowa
Zapewne najczęściej spotykałeś/aś się z miarą kątów podawaną w stopniach. Miara łukowa, o której tu mowa, podawana jest w radianach. Jak wyznaczyć miarę łukową?
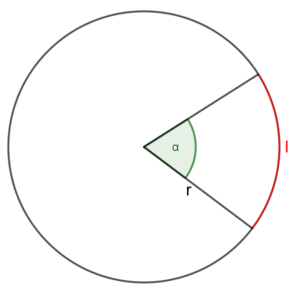
Powstał łuk długości $l$.
Miara łukowa $α$ to stosunek długości $l$ wyciętego przez ten kąt do długości promienia $r$.
$$\Large{α = \frac {l}{r} rad}$$
Wstawiając do wzoru $r = \frac {3}{2}$, $l = \frac{π}{3}$.
$α = \frac {l}{r}$$ = \frac {\frac{π}{3}}{\frac {3}{2}}$$ = \frac{π}{3} \cdot \frac{2}{3}$$ = \frac {2}{9} π$
Odpowiedź: Miara łukowa kąta $α$ wynosi $\frac {2}{9} π$.
Rysujemy okrąg o promieniu $r=1$ (jednostkowy) i zaznaczamy kąt półpełny.

Wstawiamy do wzoru:
$α = \frac {l}{r}$$ = \frac{\frac{180°}{360°} \cdot 2π \cdot r}{r}$$ = \frac{180°}{360°} \cdot 2π$$ = \frac{360°}{360°} \cdot π$$ = π$
Uwaga: Postępując analogicznie wyznaczamy miary kątów :
- prostego $90° = \frac {π}{2}$
- pełnego $360° = 2π$
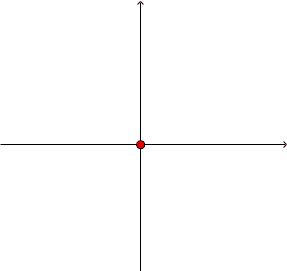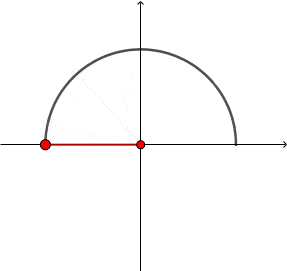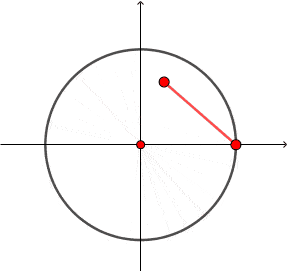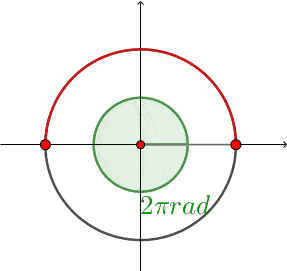
Zamiana stopni na radiany
Musisz zapamiętać, że $360° = 2π$ (lub stąd $180° = π$)
Łatwo wyznaczysz miarę kąta stosując wzór $α (rad) = \frac {α(°) \cdot π}{180°} rad$ lub stosując proporcję.
Wstawiamy do wzoru:
$α (rad) = \frac {α(°) \cdot π}{180°} $$ = \frac {235° \cdot π}{180°} $$ = \frac{47}{36} π rad$
Układamy proporcję:
$180° – π$
$60° – α$
$α = \frac{60° \cdot π}{180°}$$ = \frac {π}{3}$
Odpowiedź: Miara łukowa kąta kąta $60°$ wynosi $\frac{π}{3}$.
Zamiana radianów na stopnie
Przekształcamy wzór wyznaczając $α(°)$
$α (rad) = \frac {α(°) \cdot π}{180°} $
$α (°) = \frac {α(rad) \cdot 180°}{π} $
$α = \frac{ \frac{2}{3} π \cdot 180°}{π}$$ = \frac{2}{3} \cdot 180°$$ = 120°$
Odpowiedź: $α = \frac{2}{3} π = 120°$.
Układamy proporcję:
$180° – π$
$α$ – $1$
$α = \frac{180°}{π}$.
Odpowiedź: Jeden radian to $\frac{180°}{π}$.
