Stożek
Stożek jest bryłą obrotową powstałą przez obrót o $360^{\circ}$ trójkąta prostokątnego dookoła prostej zawierającej jedną z przyprostokątnych tego trójkąta.
- przyprostokątna trójkąta zawarta w osi obrotu jest wysokością ostrosłupa, oznaczamy ją przez $h.$
- przyprostokątna trójkąta, która nie jest zawarta w osi obrotu jest promieniem podstawy stożka, oznaczamy ja przez $r.$
- Przeciwprostokątna tego trójkąta jest tworzącą stożka, oznaczamy ją przez $l.$
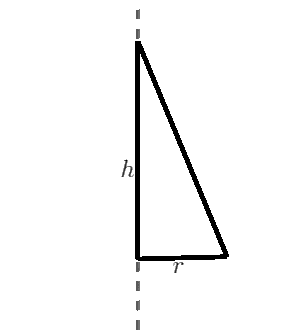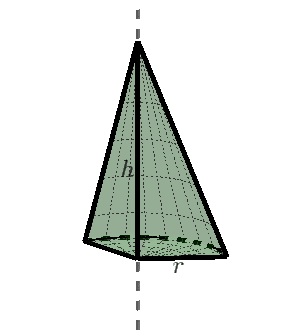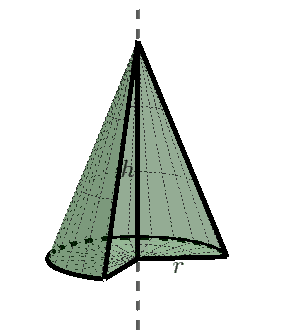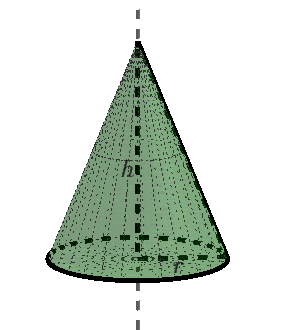
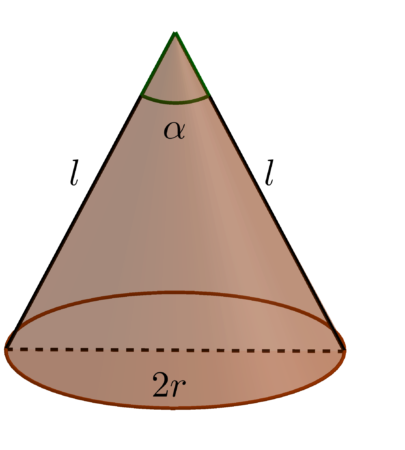
Przekrój osiowy stożka i kąt rozwarcia stożka
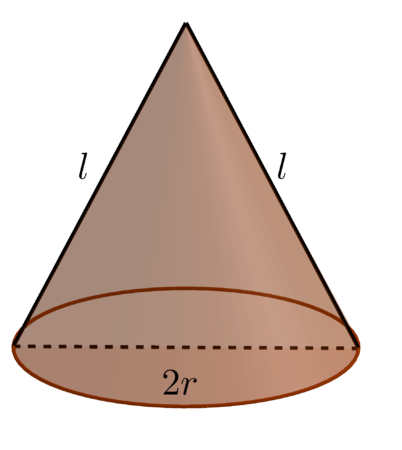
Jeżeli wyobrazimy sobie, że nas stożek jest stożkiem drogowym, to przekrój osiowy stożka jest trójkątem, który widzimy, gdy ktoś przetnie ten stożek dokładnie na pół tnąc równolegle do osi obrotu.

Objętość stożka
Objętość stożka podobnie jak w przy ostrosłupach korzystając ze wzoru:
Różnica polega na tym, że podstawą stożka jest koło, zatem:
Objętość stożka wyraża się wzorem:
$$V=\frac{1}{3}\underbrace{\pi r^2}_{Pole\: podstawy}\cdot h$$
Pole powierzchni bocznej stożka/Pole powierzchni całkowitej stożka
Jak można odczytać z zamieszczonego wyżej rysunku siatki, po „rozwinięciu” stożka powierzchnią boczną stożka jest wycinek koła o promieniu $l.$
$$P_{B}=\pi rl$$
Spróbujmy wyprowadzić powyższy wzór znając promień podstawy stożka i tworzącą stożka.
Zauważmy, że pole powierzchni bocznej stożka określa wzór $P_{B}=\frac{\alpha}{360^\circ}\cdot \pi l^2.$ Niestety nie znamy kąta $\alpha.$ Jeśli zauważymy, że we wzorze na pole wycinka koła proporcja $\frac{\alpha}{360^\circ}$ odpowiada proporcji $\frac{Długość\: łuku\: wycinka\: koła}{Obwód\: pełnego\: koła},$ to dla naszego przypadku możemy zapisać zależność: $\frac{\alpha}{360^\circ}=\frac{2\pi r}{2\pi l}.$ Stąd mamy:
$$P_{B}=\frac{2\pi r}{2\pi l}\cdot \pi l^2=\pi rl$$
Pole powierzchni całkowitej stożka określa się jako:
Czyi po prostu:
$$P_{C}=\pi r(r+l)$$
Faktycznie:
$P_{C}=\underbrace{\pi r^2}_{Pole\: podstawy}+\underbrace{\pi rl}_{Pole\: boczne}=\pi r(r+l)$
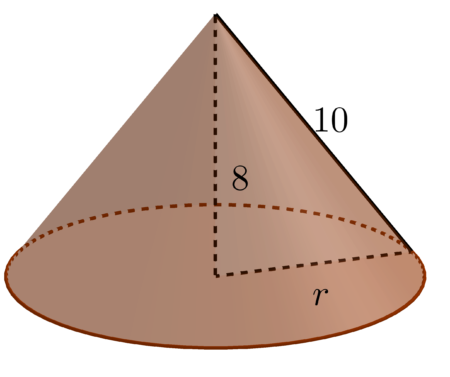
Aby policzyć objętość stożka potrzebna jest nam długość promienia podstawy stożka, policzymy ją z twierdzenia Pitagorasa.
$r^2+8^2=10^2$
$r^2+64=100$
$r^2=36$
$r=6\quad \vee \quad r=-6$
Długość musi być wartością nieujemną, zatem $r=6.$
Podstawiając wyliczoną wartość do wzory na objętość stożka otrzymujemy:
$V=\frac{1}{3}\pi r^2 h=\frac{1}{3}\pi 6^2\cdot 8=96\pi $
Odpowiedź: Objętość podanego stożka, to $96\pi .$
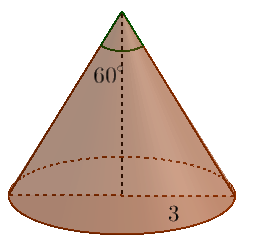
Zauważmy, że skoro kąt rozwarcia stożka ma miarę$60^{\circ },$ to przekrój osiowy stożka musi być trójkątem równobocznym, jeśli dodatkowo wiemy, że promień podstawy stożka ma długość 3, to długość boku przekroju osiowego stożka musi mieć długość 6. Ze wzoru na wysokość trójkąta równobocznego mamy:
$h=\frac{3\sqrt{3}}{2}$
Ze wzoru na pole powierzchni całkowitej stożka mamy:
$P_{C}=\pi r(r+l)=\pi 3(3+6)=27\pi$
Ze wzoru na objętość stożka mamy:
$V=\frac{1}{3}\pi r^2h=\frac{1}{3}\pi 9\frac{3\sqrt{3}}{2}=\frac{9\sqrt{3}}{2}\pi$
Odpowiedź: Pole powierzchni całkowitej tego stożka jest równe $27\pi ,$ a jego objętość, to $\frac{9\sqrt{3}}{2}\pi .$

Z zależności trygonometrycznych mamy:
$\frac{h}{8}=sin60^{\circ}$
$\frac{h}{8}=\frac{\sqrt3}{2}$
$h=4\sqrt3$
oraz
$\frac{2a}{8}=cos60^{\circ}$
$\frac{a}{4}=\frac{1}{2}$
$a=2$
Aby obliczyć $x$ pozostaje skorzystać z twierdzenia Pitagorasa dla trójkąta o bokach $h,x,a.$
$h^2+a^2=x^2$
$(4\sqrt3 )^2 +2^2=x^2$
$48+4=x^2$
$52=x^2$
$x=\sqrt{52}\quad \vee \quad x=-\sqrt{52}$
Ponieważ długość musi być nieujemna:
$x=\sqrt{52}=\sqrt{4\cdot 13}=2\sqrt{13}$
Odpowiedź: Długość szukanego odcinka, to $2\sqrt{13} .$
