Sześcian
Sześcianem nazywamy prostopadłościan, którego wszystkie krawędzie są równej długości.
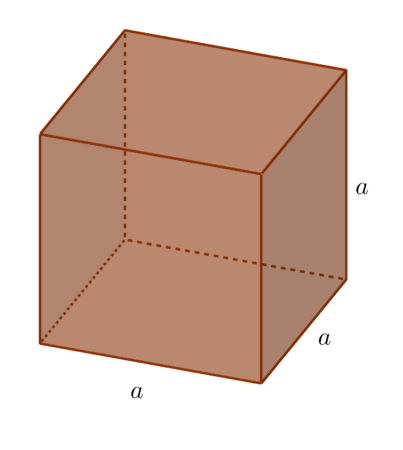

Wprost z definicji widać, że sześcian jest szczególnym przypadkiem prostopadłościanu, oraz szczególnym przypadkiem graniastosłupa prawidłowego czworokątnego, tzn.
- każdy sześcian jest graniastosłupem prawidłowym czworokątnym.
- każdy graniastosłup prawidłowy czworokątny jest prostopadłościanem.
Sześcian ma zawsze
- 6 ścian
- 12 krawędzi
- 8 wierzchołków
Ponieważ sześcian jest prostopadłościanem, pojęcie „przekątnej” odnosi się również do sześcianu, tzn. możemy zdefiniować:
Przekątną sześcianu nazywamy odcinek łączący dwa jego przeciwległe wierzchołki.
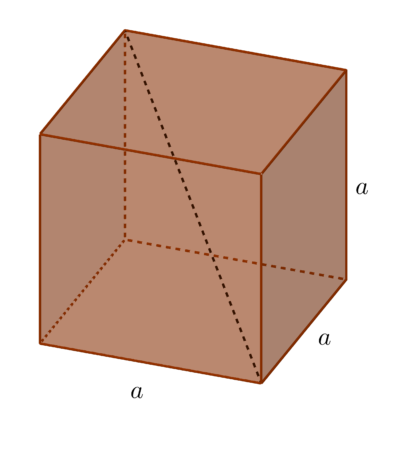

Wartym uwagi faktem jest to, że dla sześcianu takiego jak poniżej, długość przekątnej sześcianu jest zawsze równa $a\sqrt{3}.$
Faktycznie z twierdzenia Pitagorasa mamy, że
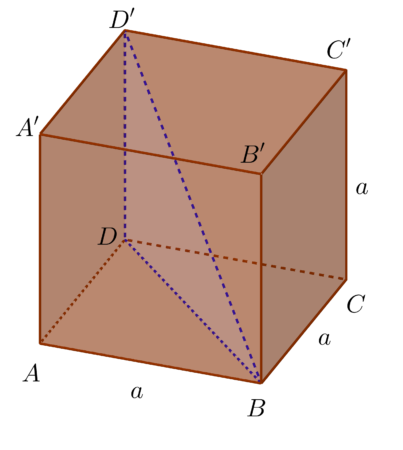

$a^2+(a\sqrt{2})^2=\mid BD^{\prime}\mid ^2$
$a^2+2a^2=\mid BD^{\prime}\mid ^2$
$\mid BD^{\prime}\mid ^2=3a^2$
$\mid BD^{\prime}\mid =a\sqrt3 \quad \vee \quad \mid BD^{\prime}\mid =-a\sqrt3$
Ponieważ długość musi być nieujemna przekątna sześcianu ma długość $a\sqrt3 .$
Faktycznie z twierdzenia Pitagorasa mamy, że

$a^2+(a\sqrt{2})^2=\mid BD^{\prime}\mid ^2$
$a^2+2a^2=\mid BD^{\prime}\mid ^2$
$\mid BD^{\prime}\mid ^2=3a^2$
$\mid BD^{\prime}\mid =a\sqrt3 \quad \vee \quad \mid BD^{\prime}\mid =-a\sqrt3$
Ponieważ długość musi być nieujemna przekątna sześcianu ma długość $a\sqrt3 .$
Korzystając ze wzorów na pole powierzchni całkowitej i objętość prostopadłościanu przyjmując $a=a^{\prime}=b^{\prime}=c^{\prime},$ gdzie $a-$ długość krawędzi sześcianu, $a^{\prime},b^{\prime},c^{\prime}-$ długości krawędzi prostopadłościanu, otrzymujemy:
Objętość sześcianu
Objętość graniastosłupa liczymy wzorem:
$Objętość=Pole\: podstawy \cdot wysokość$
W przypadku sześcianu mamy:
$Pole\: podstawy=a^2$
Zatem:
Objętość sześcianu określa się wzorem:
$$V=a^3$$
gdzie $a$ jest długością krawędzi sześcianu.
$$V=a^3$$
gdzie $a$ jest długością krawędzi sześcianu.
Pole powierzchni całkowitej sześcianu
$Pole\: powierzchni\: całkowitej=Pole\: powierzchni\: bocznej+2\cdot Pole\: podstawy$
$Pole\: powierzchni\: bocznej=a^2+a^2+a^2+a^2=4 \cdot a^2$
$Pole\: podstawy=a^2$
Pole powierzchni całkowitej sześcianu określa się wzorem:
$$P_{C}=6a^2$$
gdzie $a$ jest długością krawędzi sześcianu.
$$P_{C}=6a^2$$
gdzie $a$ jest długością krawędzi sześcianu.
Przykład 1: Oblicz pole powierzchni całkowitej oraz objętość sześcianu o krawędzi długości 4.
Korzystając ze wzorów na pole powierzchni całkowitej i objętość sześcianu mamy:
$P_{C}=6a^2=6\cdot 4^2=6\cdot 16=96$
$V=a^3=4^3=64$
Odpowiedź: Pole powierzchni całkowitej podanego sześcianu to 96, a jego objętość to 64.
$P_{C}=6a^2=6\cdot 4^2=6\cdot 16=96$
$V=a^3=4^3=64$
Odpowiedź: Pole powierzchni całkowitej podanego sześcianu to 96, a jego objętość to 64.
Przykład 2: Oblicz długość krawędzi sześcianu, którego przekątna jest o 1 dłuższa od jego krawędzi.
Narysujmy obrazek poglądowy:
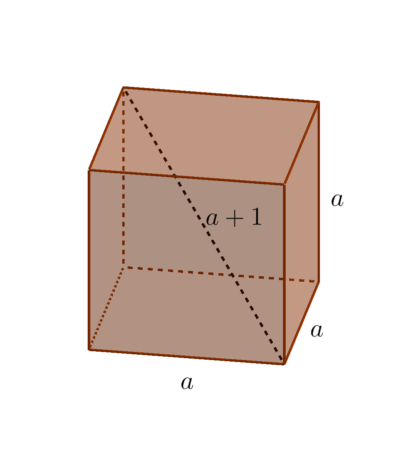
Z wyprowadzonego wcześniej wzoru na długość przekątnej sześcianu mamy:
$a\sqrt3=a+1$
$a\sqrt3-a=1$
$a(\sqrt3-1)=1$
$a=\frac{1}{\sqrt3-1}=\frac{1(\sqrt3+1)}{(\sqrt3-1)(\sqrt3+1)}=\frac{\sqrt3+1}{3-1}=\frac{1+\sqrt3}{2}$
Odpowiedź: Krawędź tego sześcianu ma długość $\frac{1+\sqrt3}{2}.$

Z wyprowadzonego wcześniej wzoru na długość przekątnej sześcianu mamy:
$a\sqrt3=a+1$
$a\sqrt3-a=1$
$a(\sqrt3-1)=1$
$a=\frac{1}{\sqrt3-1}=\frac{1(\sqrt3+1)}{(\sqrt3-1)(\sqrt3+1)}=\frac{\sqrt3+1}{3-1}=\frac{1+\sqrt3}{2}$
Odpowiedź: Krawędź tego sześcianu ma długość $\frac{1+\sqrt3}{2}.$
7+
