Trójkąty charakterystyczne to
- trójkąt o kątach $30°$, $60°$, $90°$
- trójkąt o kątach $45°$, $45°$, $90°$
Trójkąt $30°, 60°, 90°$ charakteryzuje się następującymi stosunkami długości boków:
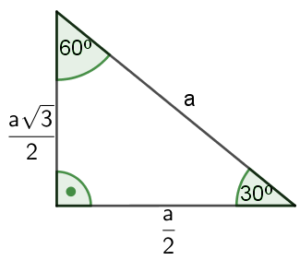
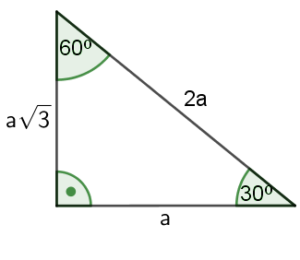
Przykład: Wyznacz długości pozostałych boków trójkąta.
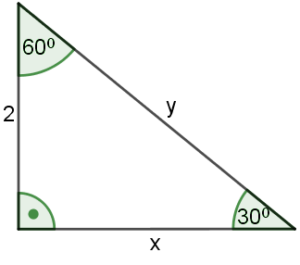
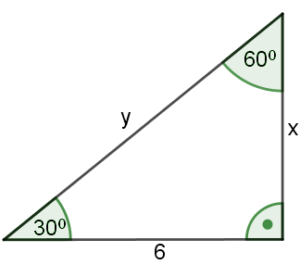
a) Znana długość przeciwprostokątnej leży naprzeciw kąta $30°$, czyli
$2 = \frac{a}{2}$
$a = 4$
Stąd: $x= \frac{a\sqrt{3}}{2}$$ = \frac{4\sqrt{3}}{2}$$ = 2\sqrt{3}$
$y = 4$
b) Znana długość przeciwprostokątnej leży naprzeciw kąta $60°$, czyli
$6 = \frac{a\sqrt{3}}{2}$
$12=a\sqrt{3}$
$a = \frac{12}{\sqrt{3}}$ $\qquad$ |usuwamy niewymierność
$a = \frac{12}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}}$$ = 4\sqrt{3}$
Stąd $x = \frac{a}{2}$$ = \frac{4\sqrt{3}}{2}$$ = 2\sqrt{3}$
$y = 4\sqrt{3}$
Przykład: W trójkącie prostokątnym jeden z boków ma miarę $30°$, a wysokość poprowadzona z wierzchołka kąta prostego jest równa $3$. Oblicz długość przyprostokątnych.
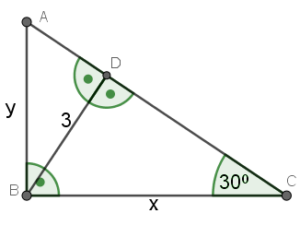
Z tego, że suma miar kątów wewnętrznych w trójkącie wynosi $180°$ mamy, że kąt przy wierzchołku A jest równy $60°$. Wiemy, że wysokość pada na podstawę pod kątem prostym. Z tego, oraz ponownie korzystając z sumy miar kątów wewnętrznych w trójkącie, mamy dwa trójkąty o kątach $30°, 60°, 90°$.

Długość $x$ jest przeciwprostokątną.
Z własności tego trójkąta: $3 = \frac{a}{2}$
$a = 6$, czyli $x = 6$

Z drugiego trójkąta mamy
$3 = \frac{a\sqrt{3}}{2}$
$6 = a\sqrt{3}$
$a = \frac{6}{\sqrt{3}}$$ = \frac{6\sqrt{3}}{3}$$ = 2\sqrt{3}$
Stąd $y = 2\sqrt{3}$
Odpowiedź: Długości przyprostokątnych trójkąta to $6$ i $2\sqrt{3}$.
Przykład: Oblicz pole i obwód trójkąta prostokątnego, którego jeden z boków ma miarę $30°$, a przeciwprostokątna jest równa $4$.
Zgodnie z oznaczeniami trójkąta pole i obwód to:
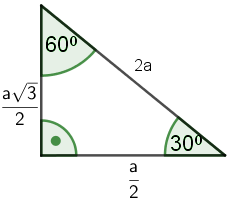
$L = a + \frac{a}{2} + \frac{a\sqrt{3}}{2}$$ = \frac{2a + a + a\sqrt{3}}{2}$$ = \frac{3a + a\sqrt{3}}{2}$$ = \frac{a(3+\sqrt3)}{2}$
$P = \frac{1}{2} \cdot \frac{a\sqrt{3}}{2} \cdot \frac{a}{2}$$ = \frac{a^2\sqrt{3}}{8}$
Podstawiając $a=4$ mamy:
$L = \frac{a(3+\sqrt3)}{2}$$ = \frac{4(3+\sqrt3)}{2}$$ = 2(3+3\sqrt{3})$
$P = \frac{a^2\sqrt{3}}{8}$$ = \frac{4^2\sqrt{3}}{8}$$ = \frac{16\sqrt{3}}{8}$$ = 2\sqrt3$
Odpowiedź: Pole tego trójkąta wynosi $2\sqrt3$, a obwód $2(3+3\sqrt{3})$.

Matura z matematyki?
Oferujemy SuperKorepetycje - korki online połączone z przejrzyście zrozumiałymi filmikami do nauki własnej
Zobacz więcej