Trójkąt prostokątny
Najpierw wprowadzimy definicję trójkąta prostokątnego.
Trójkąt prostokątny jest to trójkąt, którego jeden z kątów wewnętrznych jest kątem prostym.


Uwaga: Mówiąc przyprostokątna nie precyzujemy o którą z dwóch przyprostokątnych nam chodzi.
Twierdzenie Pitagorasa
Twierdzenie Pitagorasa będziemy wykorzystywać do obliczania długości jednego boku trójkąta znając długości dwóch pozostałych boków. Możemy z niego korzystać tylko dla trójkątów prostokątnych.
Twierdzenie Pitagorasa
Jeżeli trójkąt jest prostokątny, to kwadrat długości przeciwprostokątnej jest równy sumie kwadratów długości przyprostokątnych.

Jeżeli trójkąt jest prostokątny, to kwadrat długości przeciwprostokątnej jest równy sumie kwadratów długości przyprostokątnych.

Przykład 1: W trójkącie prostokątnym przyprostokątne mają długość 4 i 5. Znajdź przeciwprostokątną.
Rozwiązanie:

Korzystamy z twierdzenia Pitagorasa:
$5^2+4^2=x^2$
$x^2=25+16$
$x^2=41$
$x=\sqrt{41}$
Odpowiedź: Przeciwprostokątna ma długość $\sqrt{41}$.

Korzystamy z twierdzenia Pitagorasa:
$5^2+4^2=x^2$
$x^2=25+16$
$x^2=41$
$x=\sqrt{41}$
Odpowiedź: Przeciwprostokątna ma długość $\sqrt{41}$.
Przykład 2: W trójkącie prostokątnym krótsza przyprostokątna ma długość 5, a przeciwprostokątna jest o 1 dłuższa niż dłuższa przyprostokątna. Znajdź długość boków tego trójkąta.
Rozwiązanie:

Korzystamy z twierdzenia Pitagorasa:
$x^2+5^2=(x+1)^2$
$x^2+25=x^2+2x+1$
$24=2x$
$x=12$
$x+1=13$
Odpowiedź: Długości boków wynoszą 5, 12 i 13.

Korzystamy z twierdzenia Pitagorasa:
$x^2+5^2=(x+1)^2$
$x^2+25=x^2+2x+1$
$24=2x$
$x=12$
$x+1=13$
Odpowiedź: Długości boków wynoszą 5, 12 i 13.
Przykład 3: Obwód trójkąta prostokątnego wynosi 30, a jego boki to: x, 17-x, 2x+3. Znajdź pole tego trójkąta.
Rozwiązanie:
Obliczmy x:
$30=x+17−x+2x+3$
$30=2x+20$
$2x=10$
$x=5$
Otrzymujemy, że miary boków są następujące: 5, 12, 13. Mamy, że
$5^2+12^2=13^2$
Zatem bok długości 13 jest przeciwprostokątną. Obliczmy pole trójkąta
$P=\frac{1}{2}\cdot5\cdot12=30$
Odpowiedź: Pole trójkąta wynosi 30.
Obliczmy x:
$30=x+17−x+2x+3$
$30=2x+20$
$2x=10$
$x=5$
Otrzymujemy, że miary boków są następujące: 5, 12, 13. Mamy, że
$5^2+12^2=13^2$
Zatem bok długości 13 jest przeciwprostokątną. Obliczmy pole trójkąta
$P=\frac{1}{2}\cdot5\cdot12=30$
Odpowiedź: Pole trójkąta wynosi 30.
Przykład 3: Na symetralnej odcinka AB obrano punkt, który jest odległy od końców odcinka o 12 cm, a od środka odcinka o 6 cm. Oblicz długość odcinka AB.
Rozwiązanie:

Korzystamy z twierdzenia Pitagorasa.
$a^2+6^2=12^2$
$a^2=144-36=108$
$a=\sqrt{108}=\sqrt{36\cdot3}=6\sqrt{3}$
Teraz policzymy długość odcinka AB.
$|AB|=2a=12\sqrt{3}$
Odpowiedź: Długość odcinka AB wynosi $12\sqrt{3}$ cm.

Korzystamy z twierdzenia Pitagorasa.
$a^2+6^2=12^2$
$a^2=144-36=108$
$a=\sqrt{108}=\sqrt{36\cdot3}=6\sqrt{3}$
Teraz policzymy długość odcinka AB.
$|AB|=2a=12\sqrt{3}$
Odpowiedź: Długość odcinka AB wynosi $12\sqrt{3}$ cm.
Przykład 4: Oblicz długości środkowych trójkąta prostokątnego o przyprostokątnych długości 6 cm i 8 cm.
Rozwiązanie:
Najpierw policzymy długość przeciwprostokątnej:
$c=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10$
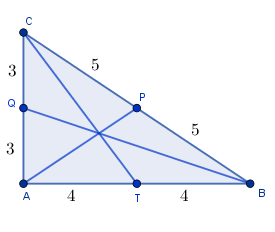
Na rysunku mamy zaznaczone środkowe trójkąta, które dzielą boki tego trójkąta na połowę. Środkowa jest to odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku. Więcej o środkowej trójkąta napisaliśmy tutaj.
Po zaznaczeniu środkowych powstało więcej trójkątów prostokątnych, dzięki czemu dalej będziemy korzystać z twierdzenia Pitagorasa.
Policzymy teraz długości środkowych tego trójkąta:
$|BQ|^2=3^2+8^2=9+64=73$
$|BQ|=\sqrt{73}$
$|CT|^2=4^2+6^2=16+36=52$
$|CT|=\sqrt{52}=\sqrt{4\cdot13}=2\sqrt{13}$
Środek okręgu opisanego na trójkącie prostokątnym jest środkiem przeciwprostokątnej, dlatego odcinki PA, PB, PC są promieniami tego okręgu. Stąd:
$|PA|=5$
Odpowiedź: Długości środkowych wynoszą $\sqrt{73}$ cm, $2\sqrt{13}$ cm oraz $5$ cm.
Najpierw policzymy długość przeciwprostokątnej:
$c=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10$

Na rysunku mamy zaznaczone środkowe trójkąta, które dzielą boki tego trójkąta na połowę. Środkowa jest to odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku. Więcej o środkowej trójkąta napisaliśmy tutaj.
Po zaznaczeniu środkowych powstało więcej trójkątów prostokątnych, dzięki czemu dalej będziemy korzystać z twierdzenia Pitagorasa.
Policzymy teraz długości środkowych tego trójkąta:
$|BQ|^2=3^2+8^2=9+64=73$
$|BQ|=\sqrt{73}$
$|CT|^2=4^2+6^2=16+36=52$
$|CT|=\sqrt{52}=\sqrt{4\cdot13}=2\sqrt{13}$
Środek okręgu opisanego na trójkącie prostokątnym jest środkiem przeciwprostokątnej, dlatego odcinki PA, PB, PC są promieniami tego okręgu. Stąd:
$|PA|=5$
Odpowiedź: Długości środkowych wynoszą $\sqrt{73}$ cm, $2\sqrt{13}$ cm oraz $5$ cm.
Uwaga: Istnieje twierdzenie odwrotne do twierdzenia Pitagorasa, które mówi nam, że jeżeli kwadrat długości przeciwprostokątnej jest równy sumie kwadratów długości przyprostokątnych to trójkąt jest prostokątny.
Twierdzenie o wysokości poprowadzonej z wierzchołka kąta prostego
Wprowadzimy teraz twierdzenie, które mówi nam o stosunku wysokości poprowadzonej z wierzchołka kąta prostego do długości przeciwprostokątnej.
Twierdzenie
Wysokość poprowadzona z wierzchołka kąta prostego dzieli dany trójkąt na dwa trójkąty podobne do niego: $\triangle{ABC}\sim\triangle{ABD}\sim\triangle{BCD}$, a ponadto $h^2=xy$.
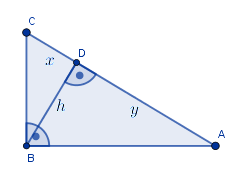
Wysokość poprowadzona z wierzchołka kąta prostego dzieli dany trójkąt na dwa trójkąty podobne do niego: $\triangle{ABC}\sim\triangle{ABD}\sim\triangle{BCD}$, a ponadto $h^2=xy$.

Uwaga: Jest to bardzo prosty wzór, o którym często zapominamy, a dzięki niemu możemy znacznie skrócić rozwiązanie zadania.
Przykład 6: W trójkącie prostokątnym przeciwprostokątna jest podzielona przez wysokość w stosunku 1:3. Oblicz stosunek długości przyprostokątnych tego trójkąta.
Rozwiązanie:
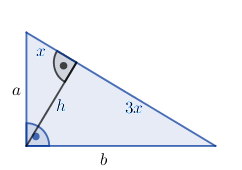
Należy policzyć $\frac{a}{b}$.
Najpierw wyznaczymy h.
$h^2=x\cdot3x$
$h^2=3x^2$
$h=x\sqrt{3}$
Teraz wyznaczymy a i b.
$a^2=h^2+x^2=3x^2+x^2=4x^2$
$a=2x$
$b^2=h^2+(3x)^2=3x^2+9x^2=12x^2=3\cdot4x^2$
$b=2x\sqrt{3}$
Zatem otrzymujemy, że
$\frac{a}{b}=\frac{2x}{2x\sqrt{3}}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.
Odpowiedź: Stosunek długości przyprostokątnych tego trójkąta wynosi $\frac{\sqrt{3}}{3}$.

Należy policzyć $\frac{a}{b}$.
Najpierw wyznaczymy h.
$h^2=x\cdot3x$
$h^2=3x^2$
$h=x\sqrt{3}$
Teraz wyznaczymy a i b.
$a^2=h^2+x^2=3x^2+x^2=4x^2$
$a=2x$
$b^2=h^2+(3x)^2=3x^2+9x^2=12x^2=3\cdot4x^2$
$b=2x\sqrt{3}$
Zatem otrzymujemy, że
$\frac{a}{b}=\frac{2x}{2x\sqrt{3}}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.
Odpowiedź: Stosunek długości przyprostokątnych tego trójkąta wynosi $\frac{\sqrt{3}}{3}$.
Przykład 7: W trójkącie prostokątnym wysokość o długości 4 cm dzieli przeciwprostokątną w stosunku 10:19 . Oblicz pole trójkąta.
Rozwiązanie:
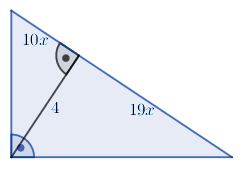
Na podstawie twierdzenia o wysokości opuszczonej na przeciwprostokątną trójkąta mamy:
$4^2=10x\cdot19x$
$16=190x^2$
$x^2=\frac{16}{190}$
$x=\frac{4}{\sqrt{190}}=\frac{4\sqrt{190}}{190}=\frac{2\sqrt{190}}{95}$
Obliczamy długość przeciwprostokątnej
$10x+19x=29x=29\cdot\frac{2\sqrt{190}}{95}=\frac{58\sqrt{190}}{95}$.
Teraz policzymy pole trójkąta.
$P=\frac{1}{2}\cdot29x\cdot4=2\cdot\frac{58\sqrt{190}}{95}=\frac{116\sqrt{190}}{95}$
Odpowiedź: Pole trójkąta wynosi $\frac{116\sqrt{190}}{95}$.

Na podstawie twierdzenia o wysokości opuszczonej na przeciwprostokątną trójkąta mamy:
$4^2=10x\cdot19x$
$16=190x^2$
$x^2=\frac{16}{190}$
$x=\frac{4}{\sqrt{190}}=\frac{4\sqrt{190}}{190}=\frac{2\sqrt{190}}{95}$
Obliczamy długość przeciwprostokątnej
$10x+19x=29x=29\cdot\frac{2\sqrt{190}}{95}=\frac{58\sqrt{190}}{95}$.
Teraz policzymy pole trójkąta.
$P=\frac{1}{2}\cdot29x\cdot4=2\cdot\frac{58\sqrt{190}}{95}=\frac{116\sqrt{190}}{95}$
Odpowiedź: Pole trójkąta wynosi $\frac{116\sqrt{190}}{95}$.
26+
