Naszym celem będzie sprowadzenie ułamków do wspólnego mianownika.
To działanie jest niezbędne np. przy dodawaniu i odejmowaniu ułamków.
Jak to zrobić?
Żeby znaleźć wspólny mianownik, to znajdujemy jego najmniejszą wspólną wielokrotność (NWW), to znaczy:
- Wypisujemy po kolei wielokrotności danych liczb. Dla 4 i 3 mamy:
4 $\rightarrow$ 4,8,12,16,20,24,…
3 $\rightarrow$ 3,6,9,12,15,18,… - Wypisujemy te wielokrotności aż do momentu, jak pierwszy raz znajdziemy wielokrotność liczb 4 i 3. Jest to liczba 12.
- Zatem NWW(4,3) $=$ 12, czyli liczba 12 jest ich wspólnym mianownikiem.
Rozszerzamy więc nasze ułamki tak, aby w mianowniku pojawiła się 12, to znaczy: $$\frac{2}{4} = \frac{2}{4} \cdot \color{blue}{\frac{3}{3}} \color{black}{= \frac{2\cdot3}{4\cdot3}=\frac{6}{12}}$$ $$\frac{1}{3} = \frac{1}{3} \cdot \color{blue}{\frac{4}{4}}\color{black}{ = \frac{1\cdot4}{3\cdot4}=\frac{4}{12}}$$Po tym procesie uzyskaliśmy wspólny mianownik. Jest to liczba 12.
Dodawanie ułamków zwykłych
Żeby wyjaśnić idee dodawania ułamków, to spójrz na powyższe przykłady.
Oblicz $\frac{1}{3} + \frac{1}{4}$.
Z poprzedniej części wiemy, że wspólnym mianownikiem 3 i 4 jest liczba 12.
Zatem:
Oblicz $1\frac{1}{5} + \frac{3}{5}$.
$$1\frac{1}{5} = \frac{1 \cdot 5 + 1}{5} = \frac{5+1}{5} = \frac{6}{5}$$Teraz możemy wykonać działanie:$$\frac{6}{5} + \frac{3}{5} = \frac{9}{5}$$
Oblicz $2\frac{1}{4} + 2\frac{1}{6}$.
$$2\frac{1}{6} = \frac{2 \cdot 6 + 1}{6} = \frac{12+1}{6} = \frac{13}{6}$$Znajdujemy NWW(4,6), tzn. wypisujemy wielokrotności liczb 4 i 6:
4 $\rightarrow$ 4,8,12,16,20,24,…
6 $\rightarrow$ 6,12,18,24,30,…
Zatem NWW(4,6) $=$ 12.
Wobec tego:
Odejmowanie ułamków zwykłych
Schemat odejmowania ułamków jest taki sam jak przy dodawaniu ułamków zwykłych.
Oblicz $\frac{3}{4} – \frac{1}{4}$.
Oblicz $\frac{1}{3} – \frac{1}{7}$.
Zatem:
Oblicz $2\frac{1}{3} – 1\frac{1}{9}$.
$$2\frac{1}{3} = \frac{2 \cdot 3 + 1}{3} = \frac{6+1}{3} = \frac{7}{3}$$ $$1\frac{1}{9} = \frac{1 \cdot 9 + 1}{3} = \frac{9+1}{9} = \frac{10}{9}$$Następnie sprowadzamy do wspólnego mianownika, licząc NWW(3,9). Tym razem
NWW(3,9) $=$ 9.
Wobec tego:
Mnożenie ułamków zwykłych
Żeby łatwiej wytłumaczyć zasadę mnożenia ułamków zwykłych, to spójrz na ten przykład:
Oblicz $2 \cdot \frac{2}{5}$.
$$\frac{a \cdot b}{c \cdot d} = \frac{a}{b} \cdot \frac{c}{d},\;\;\;\;gdzie: c, d \neq 0$$mamy:$$2 \cdot \frac{2}{5} = \frac{2}{1} \cdot \frac{2}{5} = \frac{2 \cdot 2}{1 \cdot 5} = \frac{4}{5}$$
Nie trzeba ich nawet sprowadzać do wspólnego mianownika.
Oblicz $2\frac{3}{4} \cdot 3\frac{2}{5}$.
Dzielenie ułamków zwykłych
Oblicz $\frac{1}{2} \div \frac{2}{3}$.
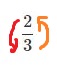
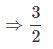
Teraz możemy obie liczby pomnożyć.
Zatem:$$\frac{1}{2} \div \frac{2}{3} = \frac{1}{2} \cdot \frac{3}{2} = \frac{1 \cdot 3}{2 \cdot 2} = \frac{3}{4}$$
Oblicz $3 \div \frac{1}{2}$.
Odwrotnością ułamka $\frac{1}{2}$ jest liczba $\frac{2}{1}$ czyli 2.
Zatem:
Oblicz $2\frac{2}{3} \div 3\frac{1}{4}$.
Zatem:
