Matura z matematyki? Poznaj nasze SuperKorepetycje! Zobacz więcej

Podstawowe wzory na pole trójkąta

1. Dowolny trójkąt – najprostszy wzór z podstawą i wysokością

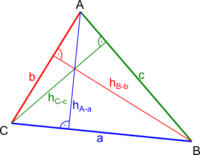
$$ P = \frac{a\cdot{h_a}}{2} = \frac{b\cdot{h_b}}{2} = \frac{c\cdot{h_c}}{2}$$
h$_a$, h$_b$, h$_c$ – wysokość w trójkącie
a, b, c – boki w trójkącie
Przykład: Oblicz pole trójkąta, gdzie a = 3 i wysokość poprowadzona na bok a wynosi 12.

Rozwiązanie:
Wystarczy podstawić wartości do wzoru i mamy gotowy wynik.
$$ P = \frac{a\cdot{h}}{2} = \frac{3\cdot{12}}{2} = 18 $$
Odp: Pole trójkąta wynosi 18.

2. Trójkąt prostokątny

trójkąt prostokątny

$$ P = \frac{a\cdot{b}}{2}$$
a = h – wysokość w trójkącie prostokątnym
b – podstawa w trójkącie prostokątnym

Przykład: Oblicz pole trójkąta prostokątnego, gdzie a = 3, b = 4, c = 5.

Rozwiązanie:

trójkąt prostokątny

Zauważmy, że najdłuższy bok
w trójkącie prostokątnym to jego
przeciwprostokątna, dalej mamy: $$a = h = 3$$ $$b = 4 $$ Skorzystajmy ze wzoru na pole
trójkąta prostokatnego$$ P = \frac{3\cdot{4}}{2} = 6 $$

Odp: Pole trójkąta prostokątnego wynosi 6.

3. Trójkąt równoboczny

trójkąt równoboczny

$$ h = \frac{a\sqrt{3}}{2} $$ $$ P = \frac{a^{2}\sqrt{3}}{4} $$
a – bok trójkąta równobocznego
h – wysokość w trójkącie równobocznym
Przykład: Oblicz pole trójkąta równobocznego, jeżeli jego wysokość ma długość 10.

Rozwiązanie:

Skorzystajmy ze wzoru na wysokość
i obliczmy a$$ 10 = \frac{a\sqrt{3}}{2} /\cdot{2} $$ $$ 20 = a\sqrt{3} /:\sqrt{3} $$ $$ \frac{20}{\sqrt{3}} = a $$ Usuwając niewymierność otrzymujemy: $$ a = \frac{20\sqrt{3}}{3}$$

Znamy długość podstawy a, zatem podstawmy ją do wzoru na pole $$ P = \frac{\left(\frac{20\sqrt{3}}{3}\right)^{2}\cdot\sqrt{3}}{4} $$ $$ P = \frac{\frac{400 \cdot 3}{9}\cdot\sqrt{3}}{4} $$ $$ P = \frac{\frac{400\sqrt{3}}{3}}{4} $$ Ostatecznie$$ P = \frac{400\sqrt{3}}{12}=\frac{100\sqrt{3}}{3} $$

Odp: Pole trójkąta równobocznego wynosi $\frac{100\sqrt{3}}{3}$ .

Pole trójkąta z wykorzystaniem sinusa

pole trójkkąta z sinusem

$$ \hspace{2cm} P=\frac{a\cdot b}{2} \cdot\sin\alpha$$
a, b – boki trójkąta
${\color[rgb]{0, 0, 0}\alpha}$ – kąt pomiędzy bokami a i b
Przykład: W trójkącie równoramiennym dany jest obwód równy 24, oraz kąt przy podstawie równy $60^{\circ}$. Oblicz pole trójkąta.

pole trójkkąta z sinusem

Zauważmy, że obwód możemy wyrazić tak
(patrz: rysunek)$$2a + 2b = 24 \Leftrightarrow a + b = 12$$

Jednocześnie zauważamy, że wysokość dzieli trójkąt na dwa trójkąty prostokątne.
Wykorzystajmy proporcję z cosinusem:
$$\frac{a}{b} = \cos60^\circ\Leftrightarrow\frac{a}{b} =\frac{1}{2}\Leftrightarrow b = 2a$$ Teraz, do równości $a + b = 12$ otrzymanej powyżej, wstawiamy $b=2a$. $$a + b = 12 \Leftrightarrow a + 2a = 12 \Leftrightarrow a= 4$$ Mając $a=4$ możemy wyznaczyć $b$: $$b = 2a \Leftrightarrow b = 8$$Korzystając ze wzoru na pole trójkąta i wiedząc, że boki mają długość $2a=8$ i $b=8$, a kąt między nimi jest równy $60^{\circ}$, otrzymujemy $$P = \frac{1}{2}\cdot2a\cdot b \cdot \sin60^\circ = \frac{1}{2}\cdot 8 \cdot 8 \cdot \frac{\sqrt{3}}{2} = 16\sqrt{3}$$
Odp: Pole trójkąta wynosi $16\sqrt{3}$.

Wzór Herona – dowolny trójkąt, znamy długości boków

$$ P = \sqrt{p\cdot(p-a)\cdot(p-b)\cdot(p-c)}$$
$$ p = \frac{a+b+c}{2}$$
p – połowa obwodu trójkąta
a, b, c – kolejno boki trójkąta
Przykład: Oblicz pole trójkąta, gdzie a = 5, b = 7, c = 8.

Rozwiązanie:

Obliczmy połowę obwodu trójkąta
$$ p = \frac{5+7+8}{2}$$ $$ p = 10 $$Zastosujmy wzór na pole dowolnego trójkąta
$$ P = \sqrt{10\cdot(10-5)\cdot(10-7)\cdot(10-8)}$$Ostatecznie
$$ P = \sqrt{300} = 2\sqrt{75} $$

Odp: Pole trójkąta wynosi $2\sqrt{75}$.

Matura z matematyki?

Oferujemy SuperKorepetycje - korki online połączone z przejrzyście zrozumiałymi filmikami do nauki własnej

Zobacz więcej
22+
Patryk Ciesielski