Zdefiniujmy na początku współczynnik korelacji liniowej Pearsona.

Współczynnik korelacji liniowej Pearsona mówi nam jaka jest siła i kierunek zależności liniowej pomiędzy 2 zmiennymi – x i y.
  • Współczynnik r przyjmuje wartości z przedziału [-1,1],
  • Im wartość bliższa 1 tym zależność jest silniejsza i dodatnia (jeżeli x rośnie to y rośnie),
  • Im wartość bliższa -1 tym zależność jest silniejsza i ujemna (jeżeli x rośnie to y maleje),
  • r=0 oznacza brak związku liniowego pomiędzy zmiennymi.

Wzory

Wzór 1 – najpopularniejszy

$$r = \frac{\sum_i\left(x_{i}-\overline{x}\right)\left(y_{i}-\overline{y}\right)}{\sqrt{\sum_i\left(x_{i}-\overline{x}\right)^{2}}\sqrt{\sum_i\left(y_{i}-\overline{y}\right)^{2}}}$$

Wzór 2

$$r=\frac{\frac{1}{n} \sum_{i=1}^{n}x_{i}y_{i}-\overline{x} \cdot \overline{y}}{\sqrt{\left(\frac{1}{n} \sum_{i=1}^{n}x_{i}^{2}-\overline{x}^{2}\right) \cdot \left(\frac{1}{n} \sum_{i=1}^{n}y_{i}^{2}-\overline{y}^{2}\right)}}$$

Wzór 3

$$r = \frac{n \cdot \sum XY – \sum X \cdot \sum Y}{\sqrt{\left[n\sum X^{2}-\left(\sum X\right)^{2}\right]}\cdot\sqrt{\left[n\sum Y^{2}-\left(\sum Y\right)^{2}\right]}}$$
Wzór 4

$$r = \frac{cov(x,y)}{\sqrt{VarX}\cdot\sqrt{VarY}}=\frac{cov(x,y)}{s(x) \cdot s(y)}$$

gdzie:

  • cov(x,y) oznacza kowariancję zmiennych $x$ i $y$,
  • s(x) – odchylenie standardowe zmiennej $x$,
  • s(y) – odchylenie standardowe zmiennej $y$,
  • VarX – wariancję zmiennej $x$,
  • VarY – wariancję zmiennej $y$.
Wzory mogą się wydajać skomplikowane, ale obliczanie współczynnika korelacji liniowej sprowadza się do zrobienia tabelki i zsumowania kolumn : )

Przykład 1.
Policzymy korelację pomiędzy zmienną X-liczba lat doświadczenia jazdy na nartach i Y- ilość złamań lub skręceń kończyny w powodu wypadku.

$x_{i}$ $y_{i}$
0 1
2 2
1 3
4 6
1 2

Na początku potrzebujemy obliczyć średnią $\overline{x}$ i $\overline{y}$:

$$\overline{x} = \frac{0+2+1+4+1}{5} = \frac{8}{5} = 1,6$$
$$\overline{y} = \frac{1+2+3+6+2}{5} = \frac{14}{5} = 2,8$$

Dalej:

  • kolumna 3. i 4. to odjęte wartości średnich od x i y.
  • kolumna 5. i 6. to kwadraty wartości w kolumnach 3. i 4.
  • kolumna 7. to iloczyn wartości z kolumn 3. i 4.

Zatem:

$x_{i}$ $y_{i}$ $x_{i}-\overline{x}$ $y_{i}-\overline{y}$ $\left(x_{i}-\overline{x}\right)^{2}$ $\left(y_{i}-\overline{y}\right)^{2}$ $\left(x_{i}-\overline{x}\right)\left(y_{i}-\overline{y}\right)$
0 1 -1,6 -1,8 2,56 3,24 2,88
2 2 0,4 -0,8 0,16 0,64 -0,32
1 3 -0,6 0,2 0,36 0,04 -0,12
4 6 2,4 3,2 5,76 10,24 7,68
1 2 -0,6 -0,8 0,36 0,64 0,48
$\sum$ – – – – 9,2 14,8 10,60

Podstawiamy do wzoru:

$$r = \frac{\sum_i\left(x_{i}-\overline{x}\right)\left(y_{i}-\overline{y}\right)}{\sqrt{\sum_i\left(x_{i}-\overline{x}\right)^{2}}\sqrt{\sum_i\left(y_{i}-\overline{y}\right)^{2}}} = \frac{10,6}{\sqrt{9,2} \cdot \sqrt{14,8}} \approx 0,9084$$

 

Odpowiedź: Współczynnik korelacji liniowej Pearsona wynosi 0,9084 co oznacza zależność silniejszą i jest ona dodatnia.

Interpretacja współczynnika korelacji liniowej Pearsona ($|r|$)

współczynnik korelacji $|r|$ interpretacja
0-0,3 słaba korelacja
0,3-0,5 korelacja umiarkowana
0,5-0,7 korelacja silna
0,7-1 korelacja bardzo silna

Wykres rozrzutu

Relację liniową jesteśmy w stanie odczytać z wykresu rozrzutu – wartości zmiennej X są na osi OX a zmiennej Y na osi OY:

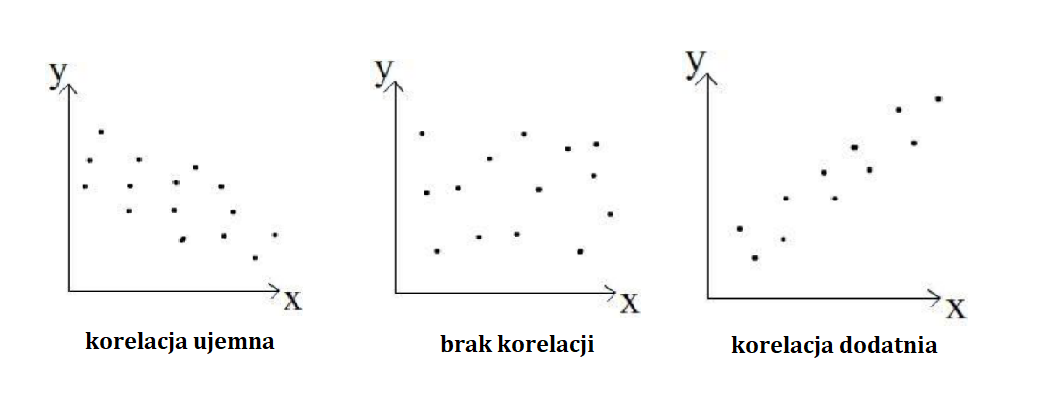
Więcej zależności pokazuje zbiór wykresów rozrzutu:


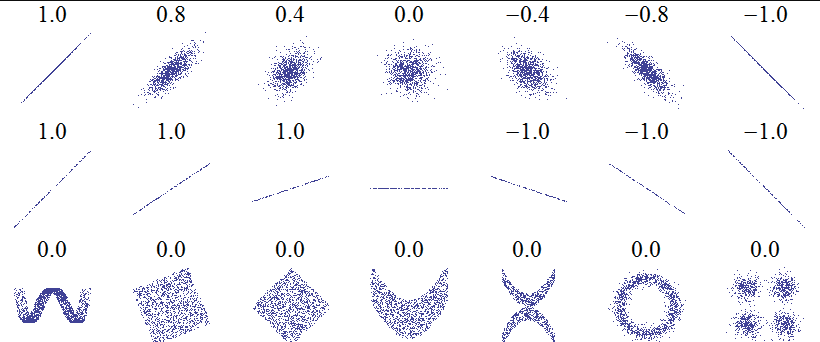
Źródło: wikipedia.org

Korelacja a regresja

Istnienie korelacji liniowej pomiędzy zmiennymi oznacza, że możemy ten związek opisać równaniem prostej regresji.
Wyznaczanie  prostej regresji dla zmiennych podanych w tabelce jest bardzo podobne co w przypadku korelacji liniowej.

Jeżeli korelacja liniowa jest dodatnia to współczynnik liniowy a regresji będzie dodatni (i odwrotnie).

Na tej stronie  wytłumaczyłem jak możemy przekształcać wzory na korelację we wzory na regresję (i odwrotnie).
Z obu pojęciami związany jest  współczynnik determinacji (zbieżności) który liczymy podnosząc współczynnik korelacji do kwadratu.
Mówi on jak dobrze dopasowany jest model regresji do danych.

Inne wzory na korelację Pearsona:

Przykład 2.
Czy istnieje liniowa zależność między liczbą nowych użytkowników (x) a liczbą nieregulaminowych tematów (y) w poszczególnych godzinach działania forum?

$i$ $x_{i}$ $y_{i}$ $x_{i}y_{i}$ $x_{i}y_{i}-\overline{x}\cdot\overline{y}$ $x_{i}^{2}$ $x_{i}^{2}-\overline{x}^{2}$ $y_{i}^{2}$ $y_{i}^{2}-\overline{y}^{2}$
1 0 1 0 -4,88 0 -2,56 1 -6,84
2 2 2 4 -0,48 4 1,44 4 -3,84
3 1 3 3 -1,48 1 -1,56 9 1,16
4 4 6 24 19,52 16 13,44 36 28,16
5 1 2 2 -2,48 1 -1,56 4 -3,84
$\sum$ 8 14 33 10,6 22 9,2 54 14,8
Dla $n=5$ średnie arytmetyczne $\overline{x}$ i $\overline{y}$ wynoszą: $$\overline{x} = \frac{1}{5} \cdot 8 = 1,6$$ $$\overline{y} = \frac{1}{5} \cdot 14 = 2,8$$ $$\overline{x}\cdot\overline{y}=4,88$$
Ze wzoru 2 mamy:

$$r = \frac{\frac{1}{5} \cdot 10,6}{\sqrt{\left(\frac{1}{5} \cdot 9,2\right)}\cdot \sqrt{\left(\frac{1}{5} \cdot 14,8\right)}} \approx 0,9084$$

Wnioski:

  • $r>0$ – korelacja dodatnia (wraz ze wzrostem liczby nowych użytkowników rośnie liczba nieregulaminowych tematów,
  • $r = 0,9084$ – zależność liniowa między liczbą nowych użytkowników a liczbą nieregulaminowych tematów jest dość silna.

 

Podstawiamy do wzoru 3:

$$r = \frac{5 \cdot 33 – 8 \cdot 14}{\sqrt{\left[5\sum 22-8^{2}\right]}\cdot\sqrt{\left[5 \cdot 54 -14^{2}\right]}} \approx 0,9084$$

Korelacja a kowariancja, wariancja i odchylenie standardowe

Zauważmy że we wzorze (2):

$$r=\frac{\frac{1}{n} \sum_{i=1}^{n}x_{i}y_{i}-\overline{x}\overline{y}}{\sqrt{\left(\frac{1}{n} \sum_{i=1}^{n}x_{i}^{2}-\overline{x}\right)^{2} \cdot \left(\frac{1}{n} \sum_{i=1}^{n}y_{i}^{2}-\overline{y}\right)^{2}}}$$

Licznik to wzór na kowariancję:

$$cov(x,y) = \frac{1}{n} \sum \left(X_{i}-\overline{X}\right)\left(Y_{i}-\overline{Y}\right) = \frac{1}{n} \sum X_{i}Y_{i} – \overline{XY}$$

A mianownik to wzór na pierwiastek iloczynów wariancji $x$ i $y$:

wzór na wariancję $x$ wzór na wariancję $y$
$s^{2} = \frac{1}{n} \sum_{i=1}^{n}\left(x_{i}^{2}-\overline{x}\right)^{2}$ $s^{2} = \frac{1}{n} \sum_{i=1}^{n}\left(y_{i}^{2}-\overline{y}\right)^{2}$
Przydaje się to w zadaniach, gdzie mamy podane rozkłady zmiennych losowych $X$ i $Y$ i mamy policzyć korelację pomiędzy nimi.

Założenia korelacji liniowej Pearsona

Abyśmy mogli liczyć współczynnik korelacji liniowej Pearsona:

  • zmienne muszą być ilościowe,
  • muszą one pochodzić z populacji o rozkładzie zbliżonym do normalnego,
  • i nie zawierać obserwacji odstających (zaburzą one wynik).

Dla cech jakościowych (lub wg. Innego podziału porządkowych), np. poziom wykształcenia, nie możemy policzyć współczynnika korelacji Pearsona, ale możemy policzyć współczynnik rang Spearmana.

Istotność korelacji

Skąd mamy wiedzieć czy obliczony współczynnik korelacji mamy traktować “na serio”?

Co świadczy “lepiej” o istniejącej korelacji? Współczynnik korelacji równy 0.4 dla 50 par zmiennych czy równy 0.5 dla 5 par zmiennych?

Możemy sprawdzić “wiarygodność” obliczonego współczynnika dla korelacji Pearsona i korelacji Spearmana korzystając z testu istotności korelacji. Wtedy możemy z pewnym przyjętym prawdopodobieństwem stwierdzić czy korelacja jest istotna statystycznie.

Bibliografia:

  • Greń Jerzy, Statystyka matematyczna: Modele i zadania, Wyd. 4, Warszawa, PWN, 1974
  • Stanisławek Jędrzej, Podstawy statystyki, Warszawa, Oficyna Wydawnicza Politechniki Warszawskiej, 2010, ISBN 978-83-7207-882-7
5+
Martyna Szczygieł