Test dla jednej średniej to najpopularniejsze zadanie na kolokwiach i egzaminach z działu wnioskowanie statystyczne.
Mamy do wyboru 3 modele:
Model 1 (rozkład normalny, znana wariancja)
- $X$ – zmienna losowa o rozkładzie normalnym $N(m,\sigma)$,
- wartość oczekiwana $m=EX$ nie jest znana,
- wariancja $\sigma^{2}=D^{2}X$ jest znana.
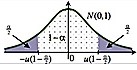
$$U = \frac{\overline{X}-m_{0}}{\sigma} \cdot \sqrt{n}$$ ma rozkład $N(0,1)$ przy założeniu prawdziwości hipotezy zerowej $H_{0}:m=m_{0}$.
|
Hipoteza |
Obszar krytyczny |
|
|
zerowa |
alternatywna |
|
| $$H_{0}: m = m_{0}$$ |
$$H_{1}: m \neq m_{0}$$ |
$$(-\infty;-U_{1-\frac{\alpha}{2}}>$$ $$\cup <U_{1-\frac{\alpha}{2}};\infty)$$ |
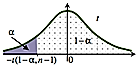
| $$H_{1}: m < m_{0}$$ | $$(-\infty;-U_{1-{\alpha}}>$$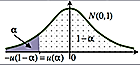 |
|
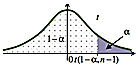
| $$H_{1}: m > m_{0}$$ | $$<U_{1-\alpha};\infty)$$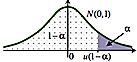 |
|
Model 2 (rozkład normalny, parametry nieznane)
- $X$ – zmienna losowa o rozkładzie normalnym $N(m,\sigma)$,
- parametry $m$ i $\sigma$ nie są znane
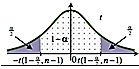
$$t = \frac{\overline{X}-m_{0}}{S} \cdot \sqrt{n-1}$$ma rozkład Studenta z $n-1$ stopniami swobody przy założeniu, że prawdziwa jest hipoteza zerowa $H_{0}:m=m_{0}$.
|
Hipoteza |
Obszar krytyczny |
|
|
zerowa |
alternatywna |
|
|
$$H_{0}: m = m_{0}$$ |
$$H_{1}: m \neq m_{0}$$ |
$$(-\infty;-t_{1-\frac{\alpha}{2},n-1}> $$$$\cup <t_{1-\frac{\alpha}{2},n-1};\infty)$$
|
|
$$H_{1}: m < m_{0}$$ |
$$(-\infty;-t_{1-\alpha,n-1}>$$
|
|
|
$$H_{1}: m > m_{0}$$ |
$$<t_{1-\alpha,n-1};\infty)$$
|
|
Model 3 (rozkład nieznany, duża próba $n \geq 30$)
W rezultacie do weryfikacji hipotez stosujemy statystykę
$$U = \frac{\overline{X}-m_{0}}{S} \cdot \sqrt{n}$$
przy założeniu, że prawdziwa jest hipoteza zerowa $H_{0}:m=m_{0}$.
|
Hipoteza |
Obszar krytyczny |
|
|
zerowa |
alternatywna |
|
| $$H_{0}: m = m_{0}$$ |
$$H_{1}: m \neq m_{0}$$ |
$$(-\infty;-U_{1-\frac{\alpha}{2}}>$$ $$\cup <U_{1-\frac{\alpha}{2}};\infty)$$ |
| $$H_{1}: m < m_{0}$$ | $$(-\infty;-U_{1-\alpha}>$$ |
|
| $$H_{1}: m > m_{0}$$ | $$<U_{1-\alpha};\infty)$$ |
|
Schemat rozwiązania jest następujący:
Krok 1:
- Wypisujemy wszystkie dane (potrzebne do policzenia statystyki testowej – może się okazać że dostaniemy jedynie szereg i np. średnią i wariancję musimy policzyć samemu).
- Zapisujemy poziom istotności $\alpha$.
- Wybieramy model i zapisujemy hipotezę zerową i alternatywną. Hipoteza alternatywna może być w postaci <>, więc trzeba zwracać uwagę na polecenie.
Krok 2:
- Zgodnie z wybranym modelem w kroku 1 zapisujemy wzór statystyki testowej a następnie podstawiamy dane i obliczamy ją.
Krok 3:
- Wyznaczamy wartość krytyczną i obszar krytyczny testu.
- Na tym etapie będziemy musieli odczytać odpowiednią wartość z tablic rozkładu normalnego lub tablic rozkładu t-Studenta
Dla testu Z będziemy używać tablic rozkładu normalnego a dla testu T tablic t-Studenta.
Krok 4:
- Jeżeli statystyka testowa (z kroku 2) należy do obszaru krytycznego (z kroku 3) to odrzucamy hipotezę zerową i przyjmujemy hipotezę alternatywną.
- Jeżeli statystyka testowa nie należy do obszaru krytycznego to nie odrzucamy hipotezy zerowej.
- Na końcu piszemy również wniosek merytoryczny dotyczący treści polecenia.
Przykłady:
$$H_{0}: m = 15$$ $$H_{1}: m < 15$$
Dane mamy dla $n=225$.
Populacja ta ma rozkład normalny oraz znana jest wariancja, więc korzystamy z modelu 1, tzn.:
Obliczamy wartość krytyczną dla $\alpha = 0,02$, korzystając z tabelki dla modelu 1 oraz z tablicy rozkładu normalnego:
$$Z_{kryt} = Z_{1-\alpha} = Z_{0,98} = 2,05$$
Zatem:
$$W_{\alpha} = \left(-\infty,-2,05\right) \ni Z$$
Odpowiedź: Obliczona statystyka testowa należy do obszary krytycznego, więc na poziomie istotności 0,02 odrzucamy hipotezę zerową $(H_{0})$ na rzecz hipotezy alternatywną $(H_{1})$. Średnia jest istotnie mniejsza od 15.
- średni wiek $\overline{x} = 38$ lata,
- $s = 4$ lata.
Na poziomie istotności $\alpha = 0,01$ zweryfikować hipotezę, że przeciętny wiek pracowników w tym zakładzie jest wyższy niż 35 lat?
$$H_{0}: m = 35$$ $$H_{1}: m > 35$$
$n=26$. Odchylenie standardowe populacji nie jest znane oraz $n<30$ (mała próba), więc korzystamy z modelu 2.
Zatem:
Obszar krytyczny $<w_{k}; \infty)$, gdzie:
$w_{k}$ – dla t-Studenta o poziomie istotności $1-\alpha = 0,99$ oraz $n-1=25$ stopni swobody mamy:
$$w_{k} = 2,485$$
Stąd:
$$t_{k} = 3,75 \in <2,485,\infty)$$
Odpowiedź: Statystyka opisowa należy do obszaru krytycznego, więc odrzucamy $H_{0}$ na rzecz $H_{1}$. Przeciętny wiek jest większy niż 35 lat.
$$H_{0}: m = 15$$ $$H_{1}: m < 15$$
Dane mamy dla $n=225$.
Populacja ta ma rozkład normalny oraz znana jest wariancja, więc korzystamy z modelu 3, tzn.:
Obliczamy wartość krytyczną dla $\alpha = 0,02$, korzystając z tabelki dla modelu 3 oraz z tablicy t-Studenta:
$$t_{kryt} = t_{1-\alpha} = t_{0,98} = 2,05$$
Zatem:
$$W_{\alpha} = \left(-\infty,-2,05\right) \ni Z$$
Odpowiedź: Obliczona statystyka testowa należy do obszary krytycznego, więc na poziomie istotności 0,02 odrzucamy hipotezę zerową $(H_{0})$ na rzecz hipotezy alternatywnej $(H_{1})$. Średnia jest istotnie mniejsza od 15.
W tym celu wylosowano próbę 6 pudełek proszku. Każde pudełko zważono i otrzymano następujące wyniki (w kg): 2,93; 2,97; 3,05; 2,91; 3,02; 2,87.
Wiadomo, że rozkład wagi pudełka z proszkiem jest normalny. Na poziomie istotności 0,01 zweryfikować hipotezę, że średnia waga pudełka jest mniejsza niż 3 kg.
Policzmy na początku średnią i odchylenie standardowe:
Ustalamy hipotezę zerową i alternatywną:
$$H_{0}: m = 3$$ $$H_{1}: m < 3$$
Dane mamy dla $n=6$.
Skorzystajmy z modelu 3, czyli:
Otrzymując z tablicy t-Studenta otrzymujemy:
Obszarem krytycznym jest przedział:
$$(-\infty;3,365> \notin t$$
Odpowiedź: Statystyka opisowa nie należy do obszaru krytycznego, więc nie ma podstaw do odrzucenia $H_{0}$. Średnia waga nie jest mniejsza niż 3 kg.