Często w poleceniach z szeregiem rozdzielczym mamy dodatkowo wyznaczyć dominantę graficznie.
Przypomnijmy, że dominantą nazywamy liczbę, która podczas badania pojawia się najczęściej.

Przykład:

Numer klasy (i) Długość konsultacji telefonicznej $(x_{0i}-x_{1i})$ Liczebność $w_{i}$
1 5-15 1
2 15-25 2
3 25-35 3
4 35-45 5
5 45-55 8
6 55-65 1
razem 20

Wiemy, że dominantę liczymy ze wzoru:

$$D_{0} = x_{0} + \frac{n_{0}-n_{-1}}{(n_{0}-n_{-1})+(n_{0}-n_{+1})}\cdot h_{0},$$

gdzie:

  • $x_{0}$ – dolna wartość przedziału dominanty,
  • $n_{0}$ – liczebność przedziału dominanty,
  • $n_{-1}$ – liczebność przedziału poprzedzającego przedział dominanty,
  • $n_{+1}$ – liczebność przedziału następującego po przedziale w którym znajduje się dominanta,
  • $h_{0}$ – rozpiętość przedziału dominanty.

 
 
U nas:

  • $x_{0} = 45$,
  • $n_{0} = 8$,
  • $n_{-1} = 5$,
  • $n_{+1} = 1$,
  • $h_{0} =10$.

 
Wobec tego:

$$D_{0} =45 + \frac{8-5}{(8-5)+(8-1)} \cdot 10 = 48$$.

 
Teraz wyznaczymy ją graficznie.
 
Zaczniemy od narysowania histogramu:


 
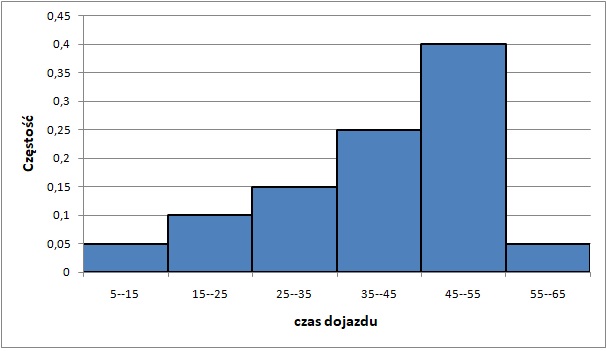
Przedziałem dominanty jest 45-55 (jest to najwyższy słupek).
 
Następnie wykonujemy operacje (patrz na gif):
 

 
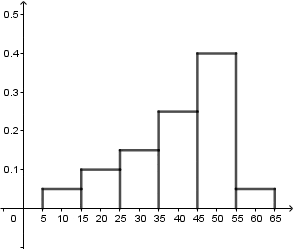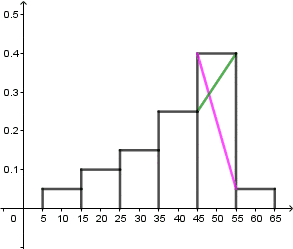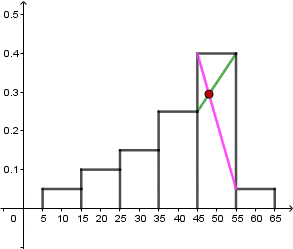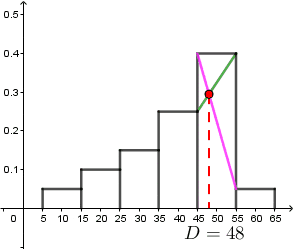
Więc dominanta jest równa: $$D=48$$.

1+
Martyna Szczygieł