Dziedzina funkcji
Zanim przejdziemy do tłumaczenia, czym jest dziedzina funkcji pomnijmy, że dla funkcji $f$ działającej ze zbioru $X$ w zbiór $Y$, dla $x\in X, y\in Y$ mamy:
$$\overbrace{f(\underbrace{x}_{Argument})}^{Wartość funkcji}=\overbrace{y}^{Wartość funkcji}$$
Dokładniejsze wyjaśnienie pojęć argumentu i wartości funkcji znajdziesz tutaj.
Dziedziną funkcji nazywamy zbiór wszystkich argumentów tej funkcji.
Czasem dziedzinę funkcji zmniejszamy tylko do interesującego nas przedziału.
Pamiętaj o tym, że punkty zaznaczone na wykresie pustym kółeczkiem nie należą do dziedziny, natomiast zamalowane tak.
Przykłady:
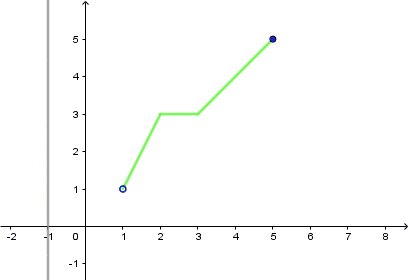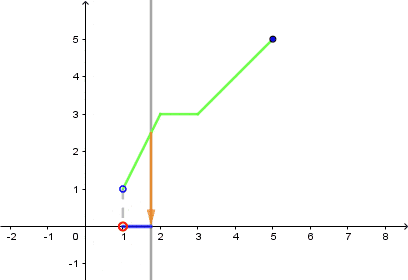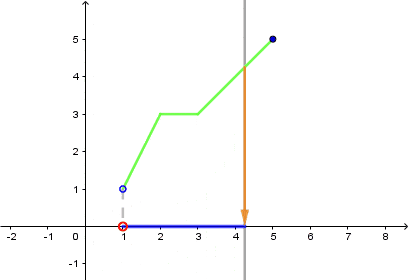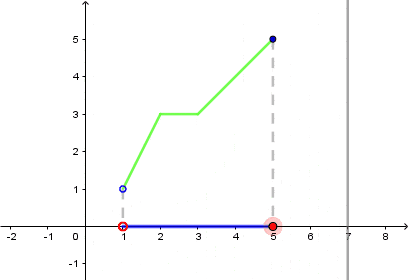
Dziedzina tej funkcji to zbiór: $(1,5>.$
Jak wyznaczyć dziedzinę funkcji?
Szukając dziedziny funkcji musimy znaleźć te $x$-sy dla których dany mamy $y$. Najłatwiej zrobić to przy pomocy opisanego niżej sposobu:
- Wyobraź sobie prostą prostopadłą do osi $OX$.
- Przesuwaj ją do lewej/do prawej.
- Gdy Twoja prosta przetnie się z wykresem funkcji, zrzutuj ten punkt na oś $OX$.
- Po wyczerpaniu się miejsc przecięcia wykresu i prostej zaznaczony przez Ciebie przedział będzie dziedziną.
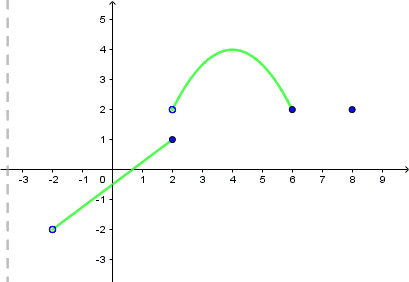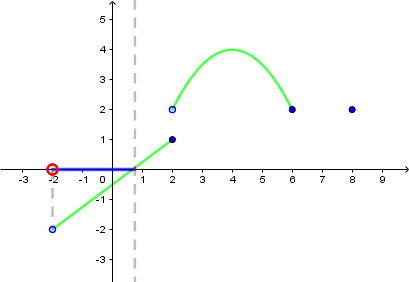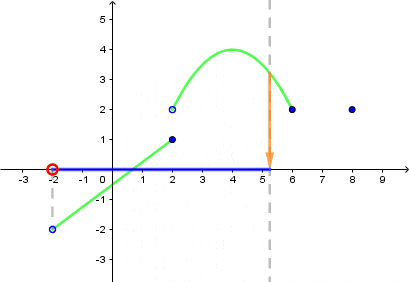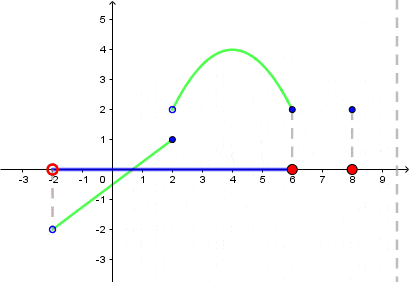
Dziedzina tej funkcji to zbiór: $(-2,6>\cup \{ 8\}.$
Zwróćmy uwagę na to, że 2 należy do dziedziny, pomimo tego, że niezamalowane kółeczko nie należy do wykresu funkcji. Dzieje się tak, gdyż zamalowane kółeczko w punkcie $(2,1)$ jest częścią funkcji.
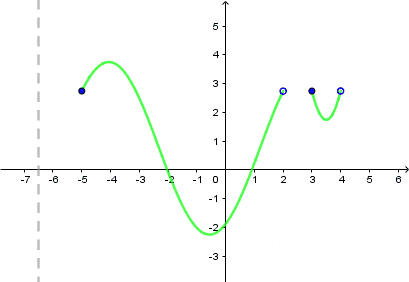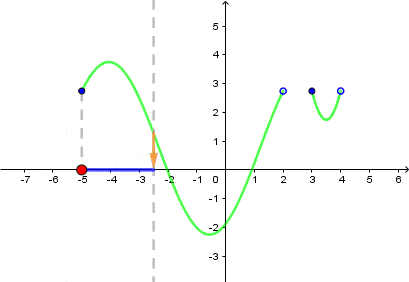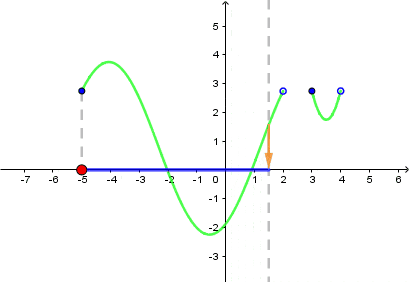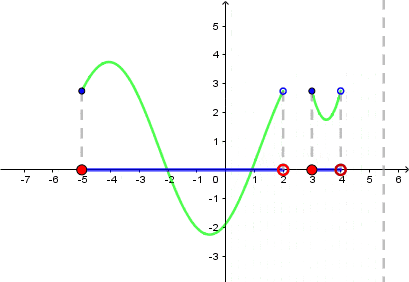
Dziedzina tej funkcji to zbiór: $<-5,2)\cup <3,4).$
18+
