Czym jest łuk?

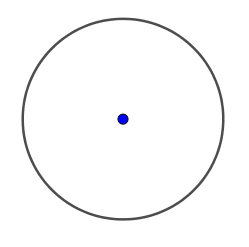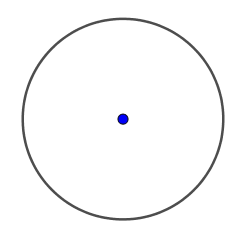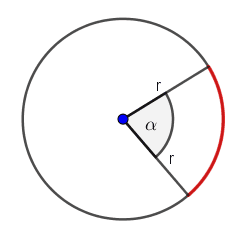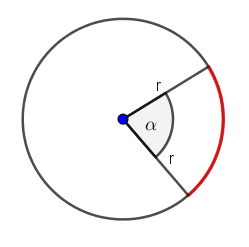
Aby wyobrazić sobie co to jest łuk poprowadź dwa promienie z środka okręgu pod pewnym kątem $α$.Te dwa promienie wycięły z okręgu łuk.

Długość łuku obliczamy ze wzoru:

$$\Large{l = \frac{α}{360°} \cdot {2π} \cdot r}$$

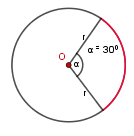
Przykład: Oblicz długość krótszego łuku wyznaczonego przez dwa promienie o długości $5$ $cm$, które są narysowane pod kątem $30°$.
Rysujemy pomocniczy szkic. Zgodnie z treścią zadania kąt między ramionami ma mierzyć $30°$, czyli:

Liczymy długość krótszego łuku (zaznaczonego na czerwono) podstawiając do wzoru $r = 5$ $cm$ i $α = 30°$.$l = \frac{30°}{360°} \cdot {2π} \cdot 5$$ = \frac{1}{12} \cdot {10π}$$ = \frac{10}{12}π$$ = \frac 56π$

Odpowiedź: Długość krótszego łuku wynosi $l = \frac 56π$ $cm$.

Styczna

Styczna to taka prosta, która ma DOKŁADNIE JEDEN punkt wspólny z okręgiem.

Ważny jest fakt, że w punkcie styczności promień pada na styczną pod kątem prostym.

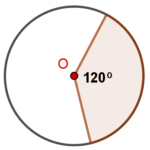
Przykład: Kąt utworzony przez dwa promienie ma miarę $120°$. Oblicz kąt, który tworzą styczne do okręgu poprowadzona przez końce tych promieni.
Zaznaczamy kąt między promieniami: $120°$

Rysujemy styczne i zaznaczamy szukany kąt.

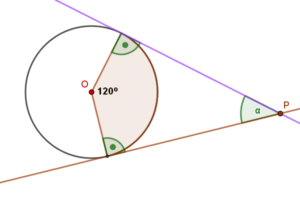
Suma kątów w czworokącie wynosi $360°$. Skoro promień pada na styczną pod kątem prostym to zadanie sprowadza się do zwykłego równania, w którym sumujemy miary kątów:$120° + 2 \cdot 90° + α = 360°$$α = 360° – (120°+2 \cdot 90°)$$= 60°$
Odpowiedź: Styczne tworzą kąt $α = 60°$.

Styczna a sieczna i cięciwa

Jeśli chodzi o sieczną, sytuacja jest o wiele prostsza, bo sieczna jest prostą, która przecina okrąg w dwóch dowolnych punktach, np.

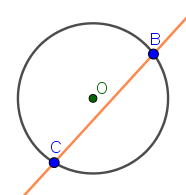
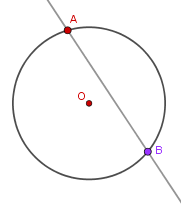
Powstały z siecznej odcinek $AB$ nazywamy cięciwą. Zauważ, że średnica okręgu też jest cięciwą (co więcej – najdłuższą z możliwych).

OGÓLNIE: Cięciwa to odcinek łączący dwa dowolne punkty okręgu.

Twierdzenie o odcinkach siecznych okręgu:

Dla punktu $P$, który nie należy do okręgu, i dwóch siecznych przecinających się w nim zachodzi zależność:

$|PA| \cdot |PB| = |PC| \cdot |PD|$

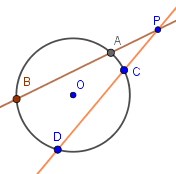
Równoważnie dla stycznej i siecznej powstaje:

$|PA|^2 = |PC| \cdot |PD|$
$|PA| \cdot |PB| = |PC| \cdot |PD|$
Przykład: Punkt $P$ leży na zewnątrz okręgu o środku $S$. Odległość punktu $P$ od środka okręgu jest trzykrotnie większa od odległości punktu $P$ od okręgu. Z punktu $P$ poprowadzono styczną do okręgu i punkt $A$ jest punktem styczności. Oblicz wartość ilorazu $\frac {|PA|}{|PS|}$.
Długość odcinka $|PB|$ to odległość punktu $P$ od okręgu, oznaczamy ją jako $a$.

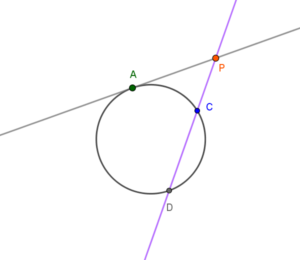
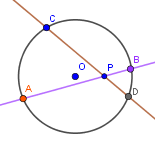
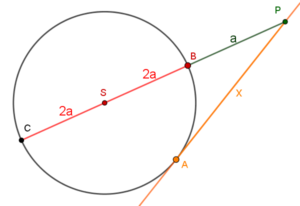
Skoro $|PS|$ jest 3-razy większy od $|PB|$ to cały odcinek $|PS|$ jest równy $3a$. Zatem skoro wiemy, że $|PB| = a$, $|PS| = 3a$, to$|SB| = 2a$ i |SB| jest promieniem okręgu, czyli wnioskujemy, że również $|CS| = 2a$ (też jest promieniem okręgu).
Niech $|AP| = x$.
Szukamy takiego ilorazu:
$\frac {|PA|}{|PS|}$$=\frac {x}{3a}$.
Z twierdzenia o odcinkach siecznej i stycznej mamy równanie:
$|PB| \cdot |PC|$$=|PA|^2$$a \cdot{5a} = x^2$
Wyliczamy $x$:
$x = \sqrt{5a^2}$$ = \sqrt{5} \cdot \sqrt{a^2}$ ($a$ jest długością odcinka, dlatego nie może być ujemny)
$x = a\sqrt{5}$

Podstawiamy do ilorazu:
$\frac {|PA|}{|PS|}$$=\frac {x}{3a}$$=\frac {a\sqrt{5}}{3a}$$=\frac {\sqrt{5}}{3}$

Odpowiedź: Szukany stosunek długości to $\frac {\sqrt{5}}{3}$.

Przykład: Odległość cięciwy $AB$ od środka okręgu wynosi $3$. Cięciwa ma długość $8$. Znajdź długość promienia tego okręgu.

Odległość punktu $O$ – środka okręgu od cięciwy jest mierzona pod kątem prostym.

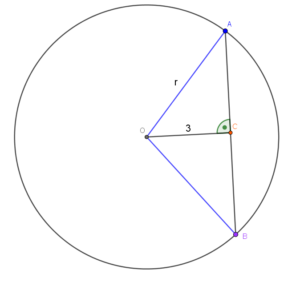
Rysujemy dowolną cięciwę $AB$. Dorysowujemy do punktów $A$ i $B$ promienie. Powstały trójkąt $OAB$ jest równoramienny ze względu na promienie, a $OC$ jest wysokością, która dzieli $AB$ na dwie równe części: $\frac {8}{2} = 4$.

Z twierdzenia Pitagorasa wyznaczamy długość promienia:

$r^2 = 3^2 + 4^2$

$r^2 = 25$

$r = 5$ (odrzucamy ujemną liczbę, bo długość nigdy nie jest z “-” ).

Odpowiedź: Długość promienia okręgu wynosi $5$.

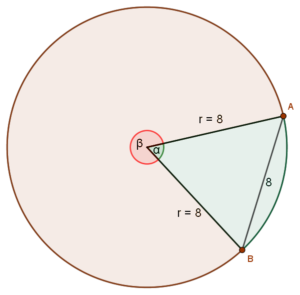
Przykład: W okręgu o promieniu $8$ $cm$ poprowadzono cięciwę o długości $8$ $cm$. Oblicz długości łuków, na które cięciwa dzieli ten okrąg.
Krok 1: Zaznaczamy na rysunku wszystkie długości:

Zauważmy, że powstaje trójkąt równoboczny, czyli w takiej sytuacji wszystkie jego kąty są równe $3α = 180°$
$α = 60°$

Krok 2: Obliczamy długość krótszego łuku:

$l_1 = \frac{60°}{360°} \cdot {2π} \cdot 8$$ = \frac{1}{6} \cdot {16π}$$ = \frac{8}{3}π$

Krok 3: Obliczamy długość dłuższego łuku:

$l_2 = \frac{300°}{360°} \cdot {2π} \cdot 8$$ = \frac{5}{6} \cdot {16π}$$ = \frac{40}{3}π$

Można również zauważyć, że długość dłuższego łuku to długość całego okręgu pomniejszona o krótszy łuk, czyli

$l_2 = 2πr – \frac{8}{3}π$$ =16π – \frac{8}{3}π$$ = \frac{40}{3}π$.

Odpowiedź: Długości łuków wynoszą $\frac{8}{3}π$ $cm$ i $\frac{40}{3}π$ $cm$.

Przykład: Dana jest długość odcinka $|AS| = 16$ $cm$ i $|AC| = 20$ $cm$. Oblicz $|BC|$, jeżeli promień jest równy $r = 8$ $cm$.

Odcinek $|AS|$ składa się z promienia i odcinka $|AD| = a$, którego długość wynosi $a = |AS| – r $$= 16 – 8 = 8$.

Dodatkowo oznaczamy $|AB| = b$, a stąd $|BC| = 20 – b$.

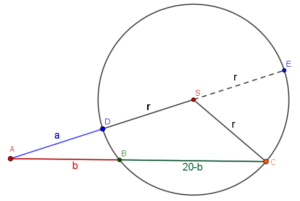
Do obliczenia $|BC|$ używamy twierdzenia i odcinkach siecznych. Żeby jednak skorzystać z tego wzoru dorysowujemy promień $r = |SE|$, czyli $|AE| = |AS| + r $$= 16 + 8 = 24$

Z twierdzenia otrzymujemy:

$|AB| \cdot |AC| = |AD| \cdot |AE|$

$b \cdot 20 = 8 \cdot 24$

$b = \frac {8 \cdot 24}{20}$$ = \frac{48}{5}$, a stąd

$|BC| = 20 – \frac{48}{5}$$= \frac{100 – 48}{5} = \frac{52}{5}$.

Odpowiedź: Długość odcinka $|BC|$ wynosi $\frac{52}{5}$ $cm$.

Przykład: Przekątna $AC$ czworokąta $ABCD$ wpisanego w okrąg jest średnicą okręgu o długości $24$ $cm$. Przekątna $BD$ dzieli $AC$ w stosunku $1:5$. Oblicz długość przekątnej $BD$ wiedząc, że krótsza część odcięta punktem przecięcia przekątnych ma długość $6$ $cm$.

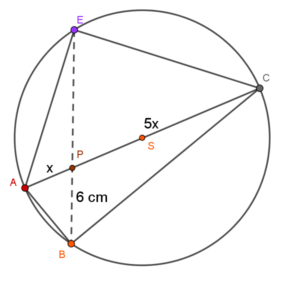
Rysujemy dowolny czworokąt tak, aby średnica była przekątną. Wyobraźmy sobie, że $|AC|$ składa się z 6 równych części, długości $x$, (bo $1 + 5 =6$). Rysujemy przekątną $|BD|$ tak, że dzieli $|AC|$ na długości $x$ i $5x$.

Wiemy, że średnica wynosi $24$ $cm$, zatem
$6x = 24$
$x = 4$ $cm$Zbierając nasze dane rysunek wygląda następująco:

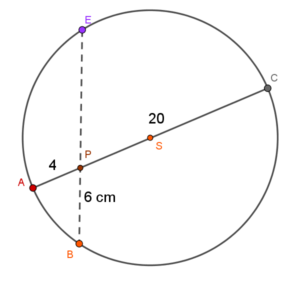
Z tw. o odcinkach siecznych:$|PA| \cdot |PC| = |PB| \cdot |PD|$
$ 4 \cdot (8 + 12) = 6 \cdot |PD|$$|PD| = \frac{4 \cdot 20}{6} = \frac{40}{3}$

Cała długość
$|BD| = |BP| + |PD| $$= 6 + \frac{40}{3} $$= \frac{18 + 40}{3}$$ = \frac{58}{3}$

Odpowiedź: Długość przekątnej |BD| wynosi $\frac{58}{3}$ $cm$.

Przykład: Cięciwy $AB$ i $CD$ okręgu o środku $S$ przecinają się w punkcie $P$. Wykaż, że trójkąty $ACP$ i $BPD$ są podobne.

>$α = β$ – to kąty wierzchołkowe

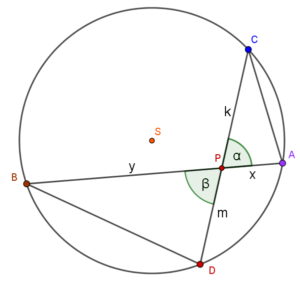
Na podstawie twierdzenia o odcinkach siecznych mamy:
$|PA| \cdot |PB| = |PC| \cdot |PD|$$ x \cdot y = k \cdot m  \hspace{0,5 cm} $ | dzielimy przez $m$ i $y$$ \frac {x}{m} = \frac {k}{y}$

W trójkątach $ACP$ i $BPD$ odpowiednie boki są proporcjonalne, a kąty zawarte między tymi bokami są równe – dlatego na mocy cechy bok-kąt-bok trójkąty $ACP$ i $BPD$ są podobne.

2+
Klaudia Mularczyk