Długość odcinka – teoria
Długość odcinka o końcach w punktach $A=(x_a,y_a)$ i $B=(x_b,y_b)$ jest dana wzorem:
Interpretacja geometryczna:
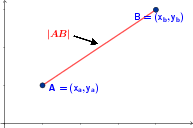
Wyznaczanie długości odcinka
Skoro $B=(-2,3)$, to $x_b=-2$, $y_b=3$.
Podstawiamy odpowiednio do wzoru na długość odcinka:
$\left|AB\right|$$=\sqrt{(x_b-x_a)^2+(y_b-y_a)^2}$$=\sqrt{(-2-0)^2+(3-5)^2}$$=\sqrt{(-2)^2+(-2)^2}$$=\sqrt8$$=2\sqrt2$
Odpowiedź: Długość odcinka o końcach w punktach $A$ i $B$ wynosi $\left|AB\right|=2\sqrt2$.
Uwaga: Długość odcinka $AB$ – $\left|AB\right|$ może być interpretowana jako “Odległość punktu $A$ od punktu $B$”. W powyższym przykładzie polecenie można zamienić na “Oblicz odległość punktu $A=(0,5)$ od punktu $B=(-2,3)$”.
Współrzędne punktów przecięcia prostej $3x+y-3=0$ z osiami układu współrzędnych możemy odczytać wprost z wykresu (nie zawsze) lub wyliczyć.
Pamiętaj! Jeżeli znasz dwa sposoby na rozwiązanie zadania, możesz samodzielnie sprawdzać swój wynik 🙂
Wyznaczymy szukane współrzędne, spróbuj odczytać je z wykresu i porównaj nasze wyniki.
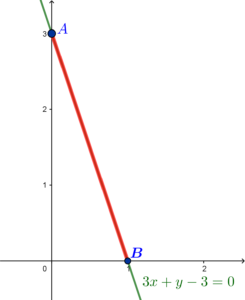
Jeżeli $x=0$ $:$ $y-3=0$, czyli $y=3$, co daje punkt $A=(0,3)$.
Jeżeli $y=0$ $:$ $3x-3=0$, czyli $3x=3$, $x=1$ co daje punkt $B=(1,0)$.
Skoro $B=(1,0)$, to $x_b=1$, $y_b=0$.
Podstawiamy odpowiednio do wzoru:
$\left|AB\right|=\sqrt{(x_b-x_a)^2+(y_b-y_a)^2}$$=\sqrt{(1-0)^2+(0-3)^2}$$=\sqrt{1^2+(-3)^2}$$=\sqrt{10}$.
.
Uwaga: Czy trójkąt jest prostokątny?
W dowolnym trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej tego trójkąta.

Zachodzi równość:
$$\Large{a^2+b^2=c^2}$$
gdzie $(c>a)\cap (c>b)$ dla przyprostokątnych $a$, $b$ i przeciwprostokątnej $c$.
Przykład: Dany jest trójkąt o wierzchołkach $A=(0,3)$, $B=(4,2)$, $C=(3,4)$. Wyznacz obwód trójkąta $ΔABC$. Czy trójkąt jest prostokątny?
$AB$, $AC$, $BC$.
Skoro $B=(4,2)$, to $x_b=4$, $y_b=2$.
Skoro $c=(3,4)$, to $x_c=3$, $y_c=4$.
Podstawiamy odpowiednio do wzoru:
$\left|AB\right|=\sqrt{(x_b-x_a)^2+(y_b-y_a)^2}$$=\sqrt{(4-0)^2+(2-3)^2}$$=\sqrt{4^2+(-1)^2}$$=\sqrt{17}$.
$\left|AC\right|=\sqrt{(x_c-x_a)^2+(y_c-y_a)^2}$$=\sqrt{(3-0)^2+(4-3)^2}$$=\sqrt{3^2+1^2}$$=\sqrt{10}$.
$\left|BC\right|\sqrt{(3-4)^2+(4-2)^2}$$=\sqrt{(-1)^2+2^2}$$=\sqrt5$.
Wyznaczamy obwód trójkąta $ΔABC$
$L$$=\left|AB\right|+\left|AC\right|+\left|BC\right|$$=\sqrt{17}+\sqrt{10}+\sqrt5$
Sprawdzamy, czy $$\left|AC\right|^2+\left|BC\right|^2=\left|AB\right|^2$$
$$\sqrt{10}^2+\sqrt5^2 \neq \sqrt{17}^2$$
$$10+5 \neq 17$$
$$15 \neq 17$$
Przykład: Znajdź pole kwadratu $ABCD$, którego dwoma sąsiednimi wierzchołkami są punkty $A=(-1,3)$ i $B=(2,1)$.
$$\left|AC\right|^2+\left|BC\right|^2=a^2$$$$2^2+3^2=a^2$$$$4+9=a^2$$$$a^2=13$$
Dla $A=(-1,3)$ i $B=(2,1)$ mamy:
$\left|AB\right|$$\sqrt{(2-(-1))^2+(1-3)^2}$$=\sqrt{13}$$
Zatem długość boku prostokąta $ABCD$ wynosi $a=\sqrt{13}$.
