Wyróżniamy następujące typy szeregów statystycznych:

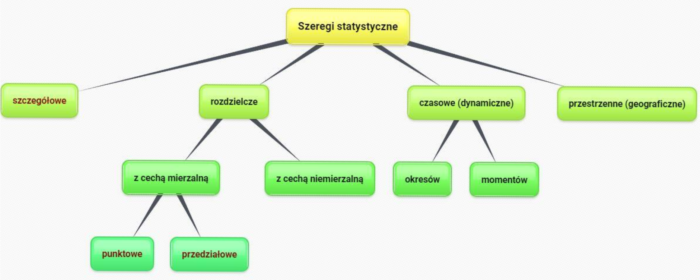
Teraz zdefiniujemy pojęcia, które są pogrubione na czerwono w powyższym schemacie.

Szereg szczegółowy (indywidualny, prosty, wyliczający) to ciąg liczbowych wielkości statystycznych uporządkowanych według badanej cechy (rosnąco lub malejąco).
W praktyce ma zastosowanie przy małych zbiorowościach.
Przykład.
Zbadano liczbę komputerów dla 6 gospodarstw domowych. Otrzymano wyniki: 2,4,3,1,2,3
Szereg szczegółowy to: 1, 2, 2, 3, 3, 4.

 

Tutaj opisałam jak liczyć kwartyle w szeregach szczegółowych.

Szereg rozdzielczy składa się z dwóch kolumn:

  • w pierwszej kolumnie znajdują się warianty badanej cechy$(x_{k})$,
  • w drugiej kolumnie liczba jednostek zbiorowości statystycznej, która posiada dany wariant cechy $(n_{k})$.

Na osobnej stronie opisałam (tutaj) jak tworzyć szeregi rozdzielcze krok po kroku jeżeli mamy podane dane.

Szeregi rozdzielcze dla cech mierzalnych dzielą się na:

  • szeregi punktowe – stosowane, gdy liczba wariantów cechy jest niewielka,
  • szeregi z przedziałami klasowymi – stosowane, gdy liczba wariantów badanej cechy jest duża.

Szereg punktowy – przykład

Liczba wizyt w teatrze

Liczba studentów

0

16

1

27

2

25

3

21

4

7

5

4

Szereg przedziałowy – przykład

Liczba dni nieobecności $x_{i}$

Liczba pracowników $n_{i}$

4 i mniej

100

5-9

150

10-14

200

15-19

130

20-24

120

Wzory

Co liczymy? Szereg przedziałowy
średnia  

$$\overline{x} = \frac{\sum x_{i} \ n_{i}}{n}$$
wariancja $$s^{2} = \frac{1}{N} \sum_{i=1}^{k} (\tilde{x} – \overline{x})^{2} \cdot n_{i}$$
dominanta $$D_{0} = x_{0} + \frac{n_{0}-n_{-1}}{(n_{0}-n_{-1})+(n_{0}-n_{+1})}\cdot h_{0}$$
mediana $$Q_{2} = x_{0Q2} + (N_{Q_{2}}-n_{isk-1}) \cdot \frac{h_{Q_{2}}}{n_{Q_{2}}}$$

Przykład 1 – szereg szczegółowy

Co liczymy?

Szereg przedziałowy

średnia

 $$\overline{x_{a}} = \frac{\sum_{i=1}^{N} x_{i}}{N}$$

wariancja

  $$s^{2} = \frac{1}{N} \sum_{i=1}^{k} (x_{i} – \overline{x})^{2}$$

dominanta

 Najczęściej powtarzająca się wartość

mediana

 Środkowa wartość
Zadanie.
Wartości temperatur (w stopniach C) zaobserwowanych w dniu 18 lipca 2009 r. o godzinie 12.00 w miastach wojewódzkich były następujące:
19, 24, 27, 27, 28, 29, 28, 29, 26, 19, 22, 25, 23, 25, 28, 26.
Na podstawie powyższych informacji należy obliczyć średnią arytmetyczną, wariancję, dominantę, medianę.

Na początku przyporządkujmy wartości rosnąco: 19, 19, 22, 23, 24, 25, 25, 26, 26, 27, 27, 28, 28, 28, 29, 29.

Średnia arytmetyczna (zwykła) wynosi:

$$\overline{x_{a}} = \frac{\sum_{i=1}^{N} x_{i}}{N} = \frac{19+…+29}{16} = \frac{405}{16} = 25,31$$

Wariancja wynosi:

$$s^{2} = \frac{1}{N} \sum_{i=1}^{k} (x_{i} – \overline{x})^{2} = \frac{(19-25,31)^{2}+…+(29-25,31)^{2}}{16} = \frac{153,44}{16} \approx 9,59$$

Średnia temperatura 18 lipca 2009 r. o godzinie 12:00 w miastach wojewódzkich wynosiła  $25,31^{\circ}$ C.
Dominanta
$D=28$.
Wśród miast wojewódzkich dominowały te, w których temperatura 18 lipca 2009 r. o godzinie 12:00 wynosiła $28^{\circ}$ C.
Mediana
Szereg parzysty (n=16), więc: $$k = \frac{N}{2} = \frac{16}{2} = 8$$

$$M_{e} = \frac{x_{k} + x_{k+1}}{2} = \frac{x_{8}+x_{9}}{2} = \frac{26+26}{2} = 26$$

W połowie miast wojewódzkich temperatura 18 lipca 2009 r. o godzinie 12:00 była nie wyżza niż $26^{\circ}$ C, a w połowie nie niższa niż $26^{\circ}$ C.

Szereg punktowy

Co liczymy?

Szereg przedziałowy

średnia

 $$\overline{x_{a}} = \frac{\sum x_{i}\cdot n_{i}}{N}$$

wariancja

 $$s^{2} = \frac{1}{N} \sum_{i=1}^{k} (x – \overline{x})^{2} \cdot n_{i}$$

dominanta

 Najczęściej powtarzająca się wartość

mediana

 Środkowa wartość

 

Przykład – szereg punktowy

Rozważmy następujące dane z tabelki:

Liczba wizyt w teatrze Liczba studentów
0 16
1 27
2 25
3 21
4 7
5 4

Policzmy średnią arytmetyczną, wariancję, medianę i dominantę.

Średnia
Korzystamy ze wzoru:
$$\overline{x_{a}} = \frac{\sum x_{i}\cdot n_{i}}{N}$$Do powyższej tabelki dokładamy kolumnę z danymi z mianownika, tzn.:

Liczba wizyt w teatrze

Liczba studentów

$x_{i}\cdot n_{i}$

0

16

0

1

27

27

2

25

50

3

21

63

4

7

28

5

4

20

$\sum$

–

188

Zatem:

$$\overline{x} = \frac{0 \cdot 16 + … + 5 \cdot 4}{16+…4} = \frac{188}{100} = 1,88$$

Wariancja
Korzystamy ze wzoru:
$$s^{2} = \frac{1}{N} \sum_{i=1}^{k} (x – \overline{x})^{2} \cdot n_{i}$$

Tworzymy tabelkę, dodając kolumnę potrzebną do policzenia $s^{2}$:

Liczba wizyt w teatrze Liczba studentów $x_{i}\cdot n_{i}$ $(x – \overline{x})^{2} \cdot n_{i}$
0 16 0 56,5504
1 27 27 20,9088
2 25 50 0,36
3 21 63 26,3424
4 7 28 31,4608
5 4 20 38,9376
$\sum$ – – 174,56

Zatem:
$$s^{2} = \frac{174.56}{100} = 1,7456$$

Mediana

Mamy łącznie $n=100$ elementów, więc pozycję mediany wyliczymy ze wzoru:
$$N_{Q_{2}} = \frac{n+1}{2} = \frac{101}{2} = 50,5$$

Mediana będzie średnią arytmetyczną 50. i 51. elementu.
Tworzymy kolumnę z wartościami skumulowanymi aby móc ocenić gdzie leży 50. i 51. element:

Liczba wizyt w teatrze

 Liczba studentów

Wartości skumulowane

0

16

16

1

27

43

2

25

68

3

21

89

4

7

96

5

4

100

Widzimy, że elementy 1 do 16 to 0, 17 do 43 to 1, 44 do 68 to 2, więc szukany 50. I 51. Element to 2 i 2.
Zatem:
$$M_{e} = \frac{x_{50}+x_{51}}{2} = 2$$

Dominanta
Dominanta jest równa 1, gdyż jest to element o największej liczebności.

Szereg rozdzielczy – wzory

Co liczymy?

Szereg przedziałowy

średnia

 $$\overline{x} = \frac{\sum x_{i} \ n_{i}}{n}$$

wariancja

  $$s^{2} = \frac{1}{N} \sum_{i=1}^{k} (\tilde{x} – \overline{x})^{2} \cdot n_{i}$$

dominanta

  $$D_{0} = x_{0} + \frac{n_{0}-n_{-1}}{(n_{0}-n_{-1})+(n_{0}-n_{+1})}\cdot h_{0}$$

mediana

 $$Q_{2} = x_{0Q2} + (N_{Q_{2}}-n_{isk-1}) \cdot \frac{h_{Q_{2}}}{n_{Q_{2}}}$$

Przykład – szereg rozdzielczy

Wysokość wydatków na pieczywo (w zł) podniesionych w grudniu 2009 r. przez 200 losowo wybranych gospodarstw domowych z Konina kształtowała się następująco:

Wydatki (w zł)

 30-40 40-50 50-60 60-70 70-80 80-90

90-100

Liczba gospodarstw

 12 25 37 62 34 22

8

Źródło: Dane umowne
W oparciu o powyższe informacje należy policzyć średnią ważoną, odchylenie standardowe i dominantę.

Tworzymy tabelkę:

Wydatki w zł $(x_{i})$

 Liczba gospodarstw $(n_{i})$ $x_{i}’$ $x_{i}\cdot n_{i}$ Wartość skumul. $x_{i} – \overline{x}$

$(x_{i} – \overline{x})^{2} \cdot n_{i}$

30-40

12

35

420

12

-28,95

10057,2

40-50

25

45

1125

37

-18,95

8977,5

50-60

37

55

2035

74

-8,95

2963,7

60-70

62

65

4030

136

1,05

68,2

70-80

34

75

2550

170

11,05

4151,4

80-90

22

85

1870

192

21,05

9748,2

90-100

8

95

760

200

31,05

7712,8

$\sum$

200

–

12790

–

–

43679,0

Średnia arytmetyczna ważona wynosi:

$$\overline{x_{a}} = \frac{\sum_{i=1}^{k} x’_{i} \cdot n_{i}}{N} = \frac{12790}{200} = 63,95$$

czyli:
Przeciętne wydatki na pieczywo poniesione w grudniu 2009 r. przez losowo wybrane gospodarstwa domowe wynosiły 63,95 zł.

Odchylenie standardowe:

$$s(x) = \sqrt{\frac{\sum_{i=1}^{k} (x’_{i} – \overline{x})^{2} \cdot n_{i}}{N}} = \sqrt{\frac{43679}{200}} = 14,78$$

czyli:
Wydatki na pieczywo w grupie losowo wybranych gospodarstw domowych odchylały się od wydatków średnich przeciętne o 14,78 zł.

Dominanta:

$$D = x_{0} + \frac{n_{0}-n_{-1}}{(n_{0}-n_{-1})+(n_{0}-n_{+1})}\cdot h_{0} = $$ $$=60 + \frac{62-37}{(62-37)+(62-34)}\cdot 10 = 64,72$$

czyli:
Wśród losowo wybranych gospodarstw dominowały te, które w grudniu 2009 r. przeznaczyły na pieczywo 64,72 zł.

 

Dokładne obliczenia dominanty w szeregu rodzielczym przedziałowym opisałam tutaj.

A tutaj opisałam, jak obliczyć kwartyle w szeregu przedziałowym.

Bibliografia:

  • Maksimowicz-Ajchel Alicja, Wstęp do statystyki: Metody opisu statystycznego, Warszawa, Wydawnictwo Uniwersytetu Warszawskiego, 2007, ISBN 978-83-235-0267-8
  • Stanisławek Jędrzej, Podstawy statystyki, Warszawa, Oficyna Wydawnicza Politechniki Warszawskiej, 2010, ISBN 978-83-7207-882-7
12+
Martyna Szczygieł