Co to jest ciąg geometryczny?

Ciągiem geometrycznym nazywamy ciąg, którego kolejne wyrazy są mnożone przez tą samą liczbę.
Liczbę tę nazywamy ilorazem ciągu. Jest ona stała, oznaczamy ją literą $q$.

Przykłady:

  • $1, 2, 4, 8, …$
  • $9, 3, 1, \frac13, \frac19, …$
  • $4, -2, 1, -\frac12, …$

Zatem $q$ w podanych przykładach:

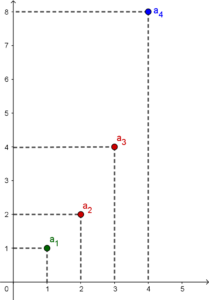
  • dla ciągu $1, 2, 4, 8, …$ → $\color{red}{q = 2}$
  • dla ciągu $9, 3, 1, \frac13, \frac19, …$ → $\color{red}{q = \frac13}$
  • dla ciągu $4, -2, 1, -\frac12, …$ → $\color{red}{q = -\frac12}$

Możemy wywnioskować prosty wzór:

$$\Large{a_{n+1} = {\color{blue}a_n }\cdot {\color{red}q}}$$
gdzie:
$a_n$ – $n$-ty wyraz ciągu
$q$ – iloraz ciągu

Uwaga: Na wykresie wyrazy ciągu geometrycznego najczęściej gwałtownie rosną lub maleją. Wykresy podanych wcześniej ciągów przedstawiają się odpowiednio:

  • Ciąg $1, 2, 4, 8, …$ o ilorazie $\color{red}{q = 2}$:
  • Ciąg $9, 3, 1, \frac13, \frac19, …$ o ilorazie $\color{red}{q = \frac13}$:
  • Ciąg $4, -2, 1, -\frac12, …$ o ilorazie $\color{red}{q = -\frac12}$:

Przykład: Dany jest ciąg geometryczny o wzorze ogólnym $a_n = (\frac12)^n$. Znajdź $a_1$, $a_5$, $a_7$.

Rozwiązując to zadanie wstawiamy liczby do wzoru:
$a_n = (\frac12)^n$
Pierwszy wyraz ciągu $a_1$:
$a_1 = (\frac12)^1 = \frac12$
Piąty wyraz ciągu $a_5$:
$a_5 = (\frac12)^5 =\frac{1}{32}$
Siódmy wyraz ciągu $a_7$:
$a_7 = (\frac12)^7 = \frac {1}{128}$
Odpowiedź: Szukane liczby to $a_1 = \frac12$, $a_5 = \frac{1}{32}$, $a_7 = \frac {1}{128}$.

Wzór ogólny ciągu geometrycznego

Wzór ogólny na $n$-ty wyraz ciągu geometrycznego wyraża się postaci:

$$\Large{a_n = {\color{blue}a_1} \cdot {\color{red}q}^{{\color{#008000}n} – 1}}$$
gdzie:
$a_1$ – pierwszy wyraz ciągu,
$q$ – różnica ciągu
$n$ – numer wyrazu, który chcemy obliczyć.

Przykład: Dany jest ciąg $5, 15, 45$. Znajdź wzór na $n$-ty wyraz tego ciągu.

Aby uzyskać wzór na $n$-ty wyraz potrzebujemy $a_1$ oraz $q$. Odczytujemy wprost, że

$a_1=5$

Aby obliczyć $q$, przekształcamy poznany na początku wzór do postaci dzieląc obie strony przez $a_n$:

$q=\frac{a_{n+1}}{a_n}$, do którego wstawiamy $a_1 = 5$ i $a_2 = 15$.

$q=\frac{15}{5} = 3$, więc $q = 3$.

Mamy już wszystko co potrzebne, wstawiamy $a_1$ i $q$ do wzoru:

$a_n = a_1 \cdot q^{n – 1} = 5 \cdot 3^{n – 1}$

Odpowiedź: Wzór na $n$-ty wyraz ciągu to $a_n = 5 \cdot 3^{n – 1}$.

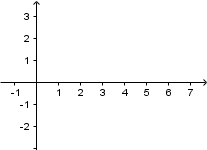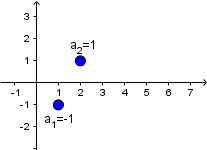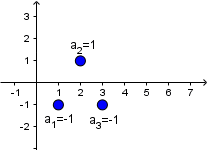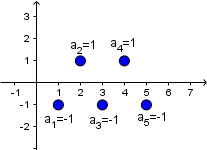
Przykład: Zaznacz na wykresie pierwsze pięć wyrazów ciągu geometrycznego, jeżeli
a) $a_n = 2^n$
b) $b_n = ( – 1 )^n$

a) $a_1 = 2^1 = 2$$a_2 = 2^2 = 4$

$a_3 = 2^3 = 8$

$a_4 = 2^4 = 16$

$a_5 = 2^5 = 32$

b) $b_1 = ( – 1 )^1 = – 1$

$b_2 = ( – 1 )^2 = 1$

$b_3 = ( – 1 )^3 = – 1$

$b_4 = ( – 1 )^4 = 1$

$b_5 = ( – 1 )^5 = – 1$

Przykład: Dany jest trzy-wyrazowy ciąg geometryczny $24, 6, a − 1$ . Ile wynosi $a$?

Krok 1: Mając podane dwa pierwsze wyrazy ciągu, wprost ze wzoru, obliczamy iloraz $q$:

$a_2 = a_1 \cdot q$

$q = \frac{a_2}{a_1}$

$q = \frac{6}{24}= \frac14$

Krok 2: Teraz możemy analogicznie wyznaczyć trzeci wyraz ciągu, ponieważ znamy już $q$ oraz mamy podane $a_1$:

$a_3 = a_1 \cdot {q^2}$

$a_3 = 24 \cdot {(\frac14)^2}$

$a_3 = \frac64 = \frac 32$

Krok 3: Skoro trzeci wyraz wyraża się w postaci $a_3 = a – 1$, to wykonujemy działanie, aby wyliczyć $a$:

$\frac32 = a – 1$

$ \frac32 + 1 = a$

$a = \frac52$

Odpowiedź: LIczba $a$ wynosi $\frac52$.

Przykład: W ciągu geometrycznym $a_n$ mamy $a_3 = 5$ i $a_4 = 15$. Ile jest równy wyraz $a_5$?

Znając $a_3$ i $a_4$ wyliczamy $q$, wiedząc, że między nimi jest jeden iloraz, czyli:
$a_4 = a_3 \cdot q$

$q = \frac{a_4}{a_3}$

$q = \frac {15}{5}= 3$

Analogicznie między $a_4$ i $a_5$ jest również jeden iloraz:

$a_5 = a_4 \cdot q$

$a_5 = 15 \cdot 3 = 45$

Odpowiedź: Wyraz piąty jest równy $a_5 = 45$.

4+
Klaudia Mularczyk