Co można odczytać z wykresu funkcji kwadratowej?
1. Dziedzina. Dla każdej funkcji kwadratowej naturalną dziedziną zawsze jest cały zbiór liczb rzeczywistych $D = \mathbb{R}$.
2. Zbiór wartości. Zbiór wartości wyznaczany jest przez współczynnik $a$ i współrzędną $q$ wierzchołka paraboli. Ma ona postać $<q , +\infty)$ dla paraboli uśmiechniętych i $(-\infty, q>$ dla paraboli smutnych. Więcej znajdziesz tutaj.
3. Najmniejsza i największa wartość. Najmniejsza/największa wartość to wartość wierzchołka. Największa jest osiągana dla paraboli o $a<0$, najmniejsza gdy $a>0$.
4. Monotoniczność. Funkcja kwadratowa nie jest monotoniczna, ale jest przedziałami monotoniczna. Monotoniczność funkcji zmienia się w wierzchołku. Dla paraboli uśmiechniętych funkcja maleje w przedziale $(-\infty, p)$ i rośnie $(p, \infty)$, dla smutnych rośnie $(-\infty, p)$ i $(p, \infty)$ maleje.
5. Miejsca zerowe. Punkty przecięcia z osią $OX$ to miejsca zerowe. Więcej znajdziesz tutaj.
6. Dla jakich argumentów funkcja przyjmuje wartości dodatnie/ujemne. Jeśli wykres jest powyżej osi $OX$ to dla tych argumentów $f(x)>0$, jeśli wykres jest poniżej osi $OX$ to $f(x)<0$.
7. Punkt przecięcia z osią $OY$. Punkt przecięcia paraboli z osią $OY$ to $(0,c)$, gdzie $c$ jest współczynnikiem ze wzoru ogólnego $f(x) = ax^2 + bx +c$.
Przykład: Odczytaj z wykresu własności funkcji kwadratowej.

1. Dziedzina: $D = \mathbb{R}$
2. Zbiór wartości: (parabola jest uśmiechnięta) $Z_w = <-9, +\infty)$
3. Najmniejsza wartość to $9$ dla argumentu $x = -2$, co możemy zapisać $f(-2)= -9$.
4. Przedziały monotoniczności: funkcja maleje w przedziale $(-\infty, -2)$, a rośnie w przedziale $(-2, +\infty)$.
5. Miejsca zerowe: $x_1 = -5$ i $x_2 = 1$.
6. Wartości dodatnie/ujemne:
funkcja przyjmuje wartości dodatnie dla $x\in(-\infty, -5)\cup(1, +\infty)$
funkcja przyjmuje wartości ujemne dla $x\in(-5, 1)$
7. Punkt przecięcia z osią $OY$: $P=(0,-5)$
Przykład: Wyznacz przedziały monotoniczności oraz zbiór wartości funkcji $f(x) = -5x^2 -15x +1$.
Współczynnik $a = -5 <0$, czyli parabola ma ramiona skierowane w dół. Do wyznaczenia przedziałów monotoniczności obliczamy $p=\frac{-b}{2a}$, czyli $x$ – ową współrzędną wierzchołka.
$p=-\frac{-15}{2 \cdot -5}$$ =-\frac{15}{10}$$ = -1,5$, zatem
funkcja rośnie w przedziale $(-\infty, -1,5)$
funkcja maleje w przedziale $(-1,5, +\infty)$
Do wyznaczenia zbioru wartości obliczamy $q$. Można to zrobić ze wzoru $q=\frac{-\Delta}{4a}$ lub skorzystać z wyznaczonego wcześniej $p$ (bo $f(p) = q$).
$f(-1,5) = -5(-1,5)^2 -15 \cdot (-1,5) + 1$$=-11,25 +22,5 +1 $$= 12,25 = 12\frac{1}{4}$
Stąd, i z tego, że $a<0$,
$Z_w = (-\infty, 12\frac{1}{4}>$.
Przykład: (CKE) Na rysunku przedstawiono fragment wykresu funkcji kwadratowej $f(x) = ax^2 + bx +c$, której miejsca zerowe to: $-3$ i $1$.
Współczynnik $c$ we wzorze jest równy
a) $1 \hspace{0,5cm}$ b) $2 \hspace{0,5cm}$ c) $3 \hspace{0,5cm}$ d) $4$
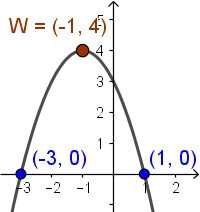
Współczynnik $c$ we wzorze wyznacza punkt przecięcia z osią $OY$, zatem odczytujemy, że $c=3$
Odpowiedź: c) $3$.
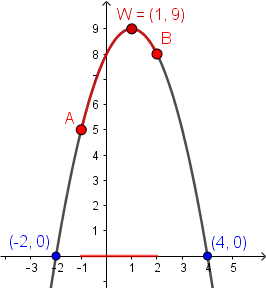
Przykład: Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej $f$. Wierzchołkiem tej paraboli jest punkt $W = (1, 9)$. Liczby $-2$ i $4$ to miejsca zerowe funkcji $f$. Wyznacz zbiór wartości funkcji $f$ oraz najmniejszą wartość funkcji $f$ w przedziale $<-1,2>$.
Zbiór wartości odczytujemy z wykresu $Z_w=(-\infty,9>$.
Zaznaczamy przedział $<-1,2>$ na osi, przenosimy na parabolę i sprawdzamy, gdzie funkcja jest najniżej. Najmniejsza wartość na danym przedziale to $5$ dla $x=-1$.