Co to jest ciąg?
Ciąg jest to szereg kolejnych liczb o danej zależności.
Przykład: Poniżej mamy przykłady ciągów:
• $1, 2, 3, 4, 5, …$ ← kolejne wyrazy zwiększają się o $1$
• $2, 5, 8, 11, 14, \ldots$ ← kolejne wyrazy zwiększają się o $3$
• $9, 9\frac12, 10, 10\frac12, 11, \ldots$ ← kolejne wyrazy zwiększają się o $\frac12$
• $- 4, – 8, – 16, – 32, – 64, \ldots$ ← kolejne wyrazy zmniejszają się o $-4$
• $10, 100, 1000, 10000, 100000, \ldots$ ← kolejne wyrazy zwiększają się $10$ razy
• $2, 5, 8, 11, 14, \ldots$ ← kolejne wyrazy zwiększają się o $3$
• $9, 9\frac12, 10, 10\frac12, 11, \ldots$ ← kolejne wyrazy zwiększają się o $\frac12$
• $- 4, – 8, – 16, – 32, – 64, \ldots$ ← kolejne wyrazy zmniejszają się o $-4$
• $10, 100, 1000, 10000, 100000, \ldots$ ← kolejne wyrazy zwiększają się $10$ razy
Kolejne liczby w ciągu nazywamy jego wyrazami. Oznaczamy je literą z dolnym indeksem.
Przykład: Mamy następujący ciąg: $- 2, 1, 4, 7, 10, \ldots$
- Pierwszy wyraz ciągu → $a_1 = – 2$.
- Drugi wyraz ciągu → $a_2 = 1$.
- Czwarty wyraz ciągu → $a_4 = 7$.
Wzór ogólny ciągu (wzór na n-ty wyraz ciągu)
Wzór ogólny jest to swojego rodzaju “przepis” na ciąg. Dzięki niemu możemy wyznaczyć dowolny wyraz tego ciągu (np. pierwszy, piąty czy setny wyraz).
Przykład: Ciąg $3, -1, -3, -5, \ldots$ ma wyraz ogólny $a_n=5-2\cdot n$.
| Jak to sprawdzić? Liczymy kolejne wyrazy podstawiając pod $n$ kolejne liczby naturalne $1, 2, 3, \ldots$: |
|
| Pierwszy wyraz ciągu to | $a_1=5-2\cdot 1= 3$ |
| Drugi wyraz ciągu to | $a_2=5-2\cdot 2=1$ |
| Trzeci wyraz ciągu to | $a_3=5-2\cdot 3=-1$ |
| Wzór ogólny pozwala nam wyznaczyć dowolny wyraz ciągu. | |
| Piętnasty wyraz to | $a_{15}=5-2\cdot 15= -25$ |
| Setny wyraz to | $a_{100}=5-2\cdot 100= -195$ |
Uwaga: W zadaniach maturalnych wzór ogólny ciągu może być nazwany wzorem na n-ty wyraz ciągu. To znaczy, że gdy mamy znaleźć wzór na n-ty wyraz ciągu, szukamy wzoru ogólnego.
Przykład: Znajdź pierwsze 3 wyrazy ciągów o podanych wzorach ogólnych: $a_n=2\cdot n – 10$, $b_n=-\frac12\cdot n+\frac32$, $c_n=3^{n-2}$.
Rozwiązując to zadanie musimy po prostu podane liczby wstawiać do wzoru ( jako $n$ ):
Dla ciągu $a_n$:
Dla ciągu $a_n$:
| Pierwszy wyraz ciągu: | $a_1=2\cdot 1 – 10= 2 – 10 = -8$ |
| Drugi wyraz ciągu: | $a_2=2\cdot 2 – 10= 4 – 10 = -6$ |
| Trzeci wyraz ciągu: | $a_3=2\cdot 3 – 10= 6 – 10 = -4$ |
Analogicznie obliczamy ciąg $b_n$ i $c_n$
| $b_1=-\frac12\cdot 1+\frac32= \frac22=1$ | $c_1=3^{1-2}= 3^{-1}=\frac13$ |
| $b_2=-\frac12\cdot 2+\frac32=\frac12$ | $c_2=3^{2-2}= 3^{0}=1$ |
| $b_3=-\frac12\cdot 3+\frac32= 0$ | $c_3=3^{3-2}= 3^{1}=3$ |
Przykład: Znajdź pierwszy, piąty i setny wyraz ciągu o wyrazie ogólnym $b_n=\frac13\cdot n+\frac23$.
Aby znaleźć te wyrazy ciągu wystarczy podstawić jedynkę, piątkę i setkę do wzoru ogólnego ciągu $b_{n}$:
| Pierwszy wyraz ciągu: | $b_1=\frac13\cdot 1+\frac23=\frac13 + \frac23=1$ |
| Piąty wyraz ciągu: | $b_5=\frac13\cdot 5+\frac23=\frac53+\frac23=\frac73=2\frac13$ |
| Setny wyraz ciągu: | $b_{100}=\frac13\cdot 100+\frac23= \frac{100}3 + \frac 23=\frac{102}3=34$ |
Przykład: Który wyraz ciągu o wzorze ogólnym $a_n=-30\cdot n + 140$ jest równy $-10$?
Rozwiązując to zadanie używamy podanego wzoru ogólnego i wstawiamy do niego $a_n$, czyli podaną liczbę $-10$. Powstanie wtedy proste równanie, gdzie jedyną niewiadomą będzie $n$ – numer wyrazu ciągu, którego wartość jest równa $-10$. Wygląda ono tak:
$-10=-30\cdot n + 140$
$-30\cdot n =-150$
$n=5$
Odpowiedź: Liczba $-10$ jest piątym wyrazem tego ciągu.
$-10=-30\cdot n + 140$
$-30\cdot n =-150$
$n=5$
Odpowiedź: Liczba $-10$ jest piątym wyrazem tego ciągu.
Wykres ciągu
Ciąg możemy potraktować jak funkcję i narysować go w układzie współrzędnych. Jego wykresem nie będzie linia, tylko zbiór punktów, gdzie na osi $OX$ zaznaczamy kolejne numery wyrazów, a na osi $OY$ ich wartości.
Przykład: Dany jest ciąg o wzorze ogólnym $a_n=2\cdot n – 3$. Oblicz wartości pierwszych trzech wyrazów.
| $a_1=2\cdot 1 – 3=-1$ | $x=1, y=-1$ ($x=1$ bo to wyraz nr 1, a $y=-1$ bo taką ma wartość pierwszy wyraz) |
| $a_2=2\cdot 2 – 3=1$ | $x=2, y=1$ |
| $a_3=2\cdot 3 – 3=3$ | $x=3, y=3$ |
Poniższy wykres ilustruje ciąg $a_{n}$:

Monotoniczność ciągu
Określając monotoniczność ciągu (dokładnie tak samo jak funkcji) po prostu stwierdzamy czy jest on rosnący, malejący czy stały.
| Ciąg rosnący – każdy jego wyraz jest większy od poprzedniego. | Ciąg malejący – każdy jego wyraz jest mniejszy od poprzedniego. | Ciąg stały – wszystkie jego wyrazy są takie same. |
| Przykład: $\frac13, 1, 3, 9, 27$ | Przykład:$ 8, 5, 2, – 1$ | Przykład: $3, 3, 3, 3$ |
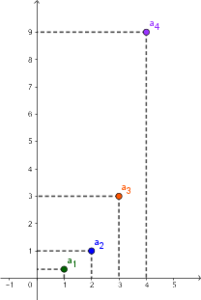 |
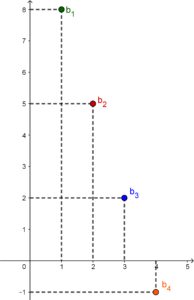 |
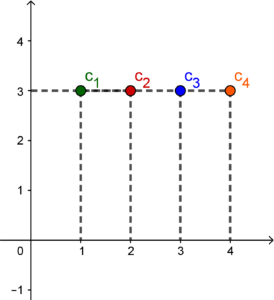 |
Ciąg nie musi być jednym z powyższych. Weźmy np. ciąg $4, -2, 1, -\frac12$( kolejne wyrazy są pomnożone przez $-\frac12$). Ciąg ten nie jest ciągiem monotonicznym, czyli ani rosnącym, ani malejącym, ani stałym.
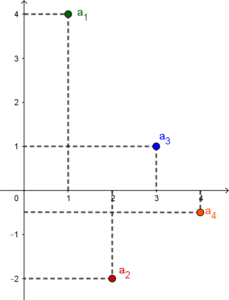
Uwaga: Określenie czy ciąg jest monotoniczny (czy jest rosnący, malejący czy stały) jest potrzebne kiedy w zadaniu obliczamy iloraz ciągu $„q”$ (przejdź do Ciąg geometryczny)
Przykład: Dany jest ciąg o wzorze ogólnym $a_n=2\cdot n – 17$. Określ czy ciąg jest rosnący, malejący czy stały.
Obliczymy trzy pierwsze wyrazy tego ciągu, dokładnie tak samo jak w poprzednich przykładach:
$a_1=2\cdot 1 – 17= 2 – 17 = – 15$
$a_2=2\cdot 2 – 17= 4 – 17 = – 13$
$a_3=2\cdot 3 – 17= 6 – 17 = – 11$
Odpowiedź: Ponieważ widzimy, że każdy wyraz jest większy od poprzedniego, to ciąg jest rosnący.
$a_1=2\cdot 1 – 17= 2 – 17 = – 15$
$a_2=2\cdot 2 – 17= 4 – 17 = – 13$
$a_3=2\cdot 3 – 17= 6 – 17 = – 11$
Odpowiedź: Ponieważ widzimy, że każdy wyraz jest większy od poprzedniego, to ciąg jest rosnący.
Przykład: Określ monotoniczność ciągu danego wzorem ogólnym $a_n=10-2\cdot n$.
Określamy monotoniczność, czyli stwierdzamy czy ciąg jest rosnący, malejący czy stały (analogicznie do poprzedniego przykładu). Wyliczamy trzy pierwsze wyrazy ciągu:
$a_1=5-2\cdot 1=10 – 2 = 8$
$a_2=5-2\cdot 2=10 – 4 = 6$
$a_3=5-2\cdot 3=10 – 6 = 4$
Odpowiedź: W tym przypadku każdy kolejny wyraz jest mniejszy od poprzednika – jest to ciąg malejący.
$a_1=5-2\cdot 1=10 – 2 = 8$
$a_2=5-2\cdot 2=10 – 4 = 6$
$a_3=5-2\cdot 3=10 – 6 = 4$
Odpowiedź: W tym przypadku każdy kolejny wyraz jest mniejszy od poprzednika – jest to ciąg malejący.
Przykład: Wzór na n-ty wyraz pewnego ciągu to $a_n=-2^{1-n}$. Czy ten ciąg jest monotoniczny?
Jak w poprzednich przykładach obliczymy trzy pierwsze wyrazy ciągu $a_{n}$:
$a_1=-2^{1-1}= -2^{0} = 1$
$a_2=-2^{1-2}= -2^{-1} = -\frac12$
$a_3=-2^{1-3}= -2^{-2} = \frac14$
W tym ciągu, mimo iż drugi wyraz jest mniejszy od poprzedniego to wyraz trzeci jest większy od drugiego. Aby ciąg był malejący to każdy jego wyraz musi być mniejszy od poprzedniego. Analogicznie, aby był rosnący to każdy jego wyraz musi być większy od poprzedniego. Dlatego nie jest to ani ciąg rosnący ani malejący. Jego wyrazy nie są też takie same, więc nie jest to także ciąg stały.
$a_1=-2^{1-1}= -2^{0} = 1$
$a_2=-2^{1-2}= -2^{-1} = -\frac12$
$a_3=-2^{1-3}= -2^{-2} = \frac14$
W tym ciągu, mimo iż drugi wyraz jest mniejszy od poprzedniego to wyraz trzeci jest większy od drugiego. Aby ciąg był malejący to każdy jego wyraz musi być mniejszy od poprzedniego. Analogicznie, aby był rosnący to każdy jego wyraz musi być większy od poprzedniego. Dlatego nie jest to ani ciąg rosnący ani malejący. Jego wyrazy nie są też takie same, więc nie jest to także ciąg stały.
Uwaga: Jeśli ciąg nie jest ani rosnący, ani malejący, ani stały, to znaczy, że nie jest monotoniczny.
4+
