Jednym z technik statystyki opisowej jest wyznaczanie miar rozkładów. Miary rozkładów dzielimy na:
Do miar rozproszenia należą między innymi:
| wariancja | Pokazuje, jak wartości danej cechy są rozrzucone (rozproszone) wokół jej średniej. |
| odchylenie standardowe | Pokazuje, jak wartości danej cechy są rozrzucone wokół jej średniej.
Różni się od wariancji tym, że jest jej pierwiastkiem. Im mniejsza wartość odchylenia tym odchylenie standardowe zbliża się do jej średniej. Im większa wartość, tym ono się oddala od jej średniej. |
| średnie odchylenie bezwzględne | Interpretacja jest podobna do odchylenia standardowego. |
| współczynnik zmienności rozkładu (klasyczny lub pozycyjny) | Bezwzględna miara zmienności rozkładu – pozwala zmierzyć w procentach jak bardzo zróżnicowany jest rozkład |
| rozstęp | Pokazuje, jaka jest największa różnica (skrajna wartość) pomiędzy najmniejszą wielkością a największą. |
| rozstęp ćwiartkowy | Pokazuje, jaka jest różnica pomiędzy kwantylem rzędu a kwantylem rzędu. |
| odchylenie ćwiartkowe | Pokazuje, gdzie się znajduję połowa rozstępu ćwiartkowego. |
Te wymienione miary rozproszenia (inaczej: zróżnicowania, dyspersji) dzielą się na:
| miary klasyczne | |
| średnie odchylenie bezwzględne (rzadko używane) | $$d = \frac{\sum_i^n|x_{i}-\bar x|}{n}$$ |
| odchylenie standardowe | $$s = \sqrt{\frac{\sum_i^n\left(x_{i}-\bar x\right)^2}{n}}$$ |
| wariancja | $$s^2 = \frac{\sum_i^n\left(x_{i}-\bar x\right)^2}{n}$$ |
| klasyczny współczynnik zmienności | $$V_s = \frac{s}{\bar x} $$ |
| miary pozycyjne | |
| rozstęp | $$R=x_{max}-x_{min}$$ |
| rozstęp ćwiartkowy | $$Q=Q_{3}-Q_{1}$$ |
| odchylenie ćwiartkowe | $$Q_{\sigma}=\frac{Q_{3}-Q_{1}}{2}$$ |
| pozycyjny współczynnik zmienności | $$V_Q = \frac{Q_{\sigma}}{Me} $$ |
gdzie $Q_{3}$ – kwantyl rzędu $\frac{3}{4}$ ; $Q_{1}$- kwantyl rzędu $\frac{1}{4}$; $\sum$- sumowanie wszystkich składników; $n$ – ilość wszystkich elementów.
Przyjmijmy, że $x_{1},…,x_{n}$ są wynikami uzyskanymi podczas badania danej cechy oraz $\bar x$ jest średnią arytmetyczną liczb $x_{1},…,x_{n}$.
Przykład
Drużyna seniorska koszykarzy KS Nędza dzieli się na dwie mniejsze drużyny: Pierwsza i Druga. W każdej drużynie jest po 10 zawodników. Ich wzrosty to:
Pierwsza: 176,181,182,187,182,195,192,200,170,185
Druga: 185,184,186,180,190,185,191,186,178,185.
Na podstawie tych danych wyliczyć miary rozproszenia.
Dla drużyny I średnia arytmetyczna wynosi:$$\bar x = \frac{176+…+185}{10}$$ $$\bar x = \frac{1850}{10}$$ $$\bar x = 185$$Analogicznie liczymy dla drużyny II:$$\bar x = 185$$Zatem średnia arytmetyczna dla obu drużyn jest taka sama.Przejdźmy do policzenia wariancji.Dla drużyny I wariancja wynosi:
$$s^2 = 71.8$$
Analogicznie liczymy dla drużyny II:
$$s^2 = 13.8$$
Jak mamy policzoną wariancję, to od razu możemy policzyć odchylenie standardowe oraz średnie odchylenie bezwzględne.
Dla drużyny I wynoszą:
$$s=\sqrt{s^{2}}=\sqrt{71.8}=8.47$$
$$d=\frac{68}{10}$$ $$d={6.8}$$
Analogicznie liczymy dla drużyny II:
$$s=\sqrt{s^{2}}=\sqrt{13.8}\approx{3.71}$$
$$d={3.6}$$
Policzmy współczynniki zmienności dla obu drużyn
$$V_{s1} = \frac{s}{\bar x} =\frac {8.47}{185}=0.0458=4.58\% $$
$$V_{s2} = \frac{s}{\bar x} =\frac {3.71}{185}=0.02=2\% $$
Współczynnik zmienności w drużynie II ma mniejszą wartość, więc w drużynie II są mniej zróżnicowane.
Zróżnicowanie w obu drużynach możemy zobaczyć na następującym wykresie.
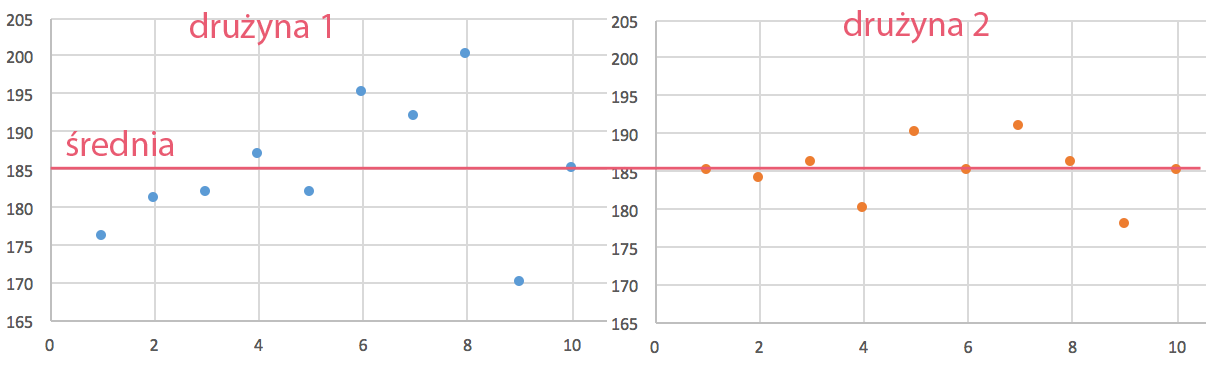
Widać, że w drugim przypadku wartości są bliżej średniej niż w pierwszym przypadku.
Liczenie pozycyjnych miar pozycyjnych wymaga najpierw wyliczenia kwartyli, co omawiamy szerzej tutaj: kwartyle w szeregu szczegółowym i kwartyle w szeregu przedziałowym
Bibliografia:
- Kopczyński Michał, Podstawy statystyki: Podręcznik dla humanistów, Warszawa, Oficyna Wydawnicza „Mówią wieki”, 2005, ISBN 83-86156-22-8
- Rószkiewicz Małgorzata, Statystyka: Kurs podstawowy, Warszawa, EFEKT, 2002, ISBN 83-87338-15-X
