Zadanie: Wzrost kobiet w pewnej populacji ma rozkład normalny $N(165, 15)$. Oznacza to, że zmienna losowa jaką jest wzrost kobiet ma rozkład normalny ze średnią równą 165 cm odchyleniem standardowym równym 15 cm. Jaki jest udział w populacji kobiet o wzroście:

  • do 160 cm
  • w przedziale 165-170 cm
  • powyżej 175 cm
  • dokładnie 150 cm
Uwaga: Więcej zagadnień matematycznych odnoszących się do powyższego zadania znajdziesz na stronie rozkład normalny.

Rozwiąż zadanie za pomocą widgetu:

Rozwiązanie:

  • Interesuje nas obliczenie prawdopodobieństwa zaznaczonego na niebiesko:

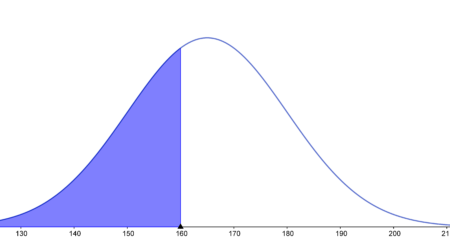
    Robimy standaryzacje zmiennej losowej:
    $$P(X < 160)=P \Big(\frac{x-\mu}{\sigma} < \frac{160-\mu}{\sigma} \Big)=$$

    Możemy wprowadzić zmienną $U$ – zmienną losową rozkładu normalnego standaryzowanego i podstawiamy dane:
    $$=P \Big(U < \frac{160-\mu}{\sigma} \Big)=P \Big(U < \frac{160-165}{15} \Big)=P(U < -0.333)=\Phi(-0.333)$$

    Uwaga:     W tablicach rozkładu normalnego najczęściej nie ma ujemnych wartości. Zatem stosujemy „przejście” w postaci: $\Phi(-\alpha)=1-\Phi(\alpha)$ bo dodatnią wartość już łatwo odnajdziemy w tablicach rozkładu normalnego.
    $$\Phi(-0.333)=1-\Phi(0.333)=1-0.6293=0.3707$$

    Odpowiedź: Szukane prawdopodobieństwo wynosi 37.07% (czyli pole zacieniowanej części wykresu wynosi 0.3707 na rysunku powyżej).

  • w przedziale 165-170 cm

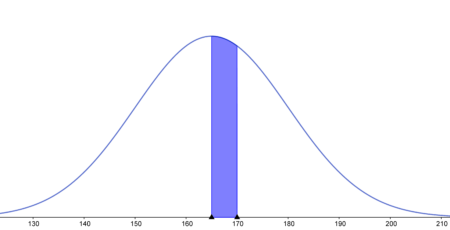
    $P(165 < X < 170)=P \Big( \frac{165-165}{15} < \frac{X-165}{15} < \frac{170-165}{15} \Big)=P(0 < X < 0.33)=$ $\Phi(0.33)-\Phi(0)=0.6293-0.5=0.1293$

    Odpowiedź: Szukane prawdopodobieństwo wynosi 12.93%.

  • powyżej 175 cm

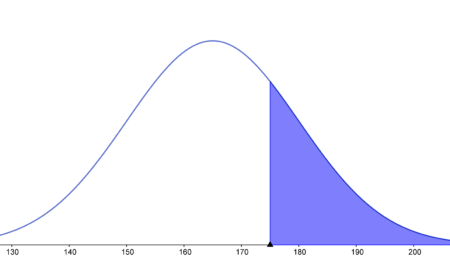
    $P(X > 175)=P \Big( \frac{X-165}{15} > \frac{175-165}{15}\Big)=P(U > 0.67)= 1-P(U < 0.67)=1-$ $\Phi(0.67)=1-0.748571=0.251429$

    Odpowiedź: Szukane prawdopodobieństwo wynosi 25.14%.

  • dokładnie 150 cm

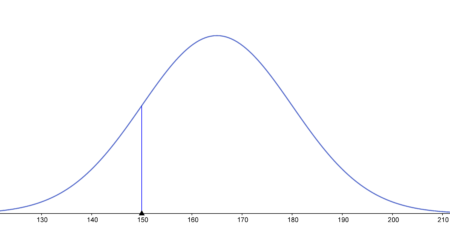
    $P(X=15)=P(150 \le X \le 150)= F(150)-F(150)=0$ (bo dla zmiennych losowych ciągłych, prawdopodobieństwo w punkcie jest równe 0)

    Odpowiedź: Prawdopodobieństwo wynosi 0.

2+
Justyna Chojecka