Metoda drzewa

W rozwiązaniu tego typu zadania pomoże nam metoda drzewa. Skonstruujmy drzewo stochastyczne ilustrujące przebieg doświadczenia losowego opisanego w poleceniu.

$1°$ Zacznijmy od początku drzewa.

$2°$ Wierzchołki drzewa po pierwszym ruchu będą opisane $O$- orzeł i $R$-reszka.

 

$3°$ Dopiszmy prawdopodobieństwa otrzymania w pierwszym rzucie orła lub reszki.

$4°$ Jeżeli wylosujemy orła możemy otrzymać orła lub reszkę, jeżeli wylosujemy reszkę możemy również otrzymać orła lub reszkę. Podobnie w kolejnym rzucie.

$5°$ Wpisujemy odpowiednie prawdopodobieństwa.

Wszystkie możliwe drogi/gałęzie drzewa możemy określić jako zbiór wszystkich zdarzeń elementarnych $Ω$. Ilość różnych dróg które możemy osiągnąć to $|Ω|$.

Tych dróg jak widać w ostatnim wierszu jest $8$, więc $|Ω|=8$.

$\color{red}{Kolorem}$ oznaczone są wszystkie gałęzie opisujące zdarzenie losowe $A$ czyli wyrzucenie orła
w drugim i trzecim rzucie.

Widzimy, że $A=${$O,O,O$}$,${$R,O,O$}, więc $A=2$

Z klasycznej definicji prawdopodobieństwa mamy: $P(A)=\frac{|A|}{|Ω|}$$=\frac28$$=\frac14$.

W bardziej skomplikowanych przypadkach skorzystamy z reguły sum dla dwóch oznaczonych gałęzi. W tym przypadku mamy $\color{blue}{\frac12+ \frac12+ \frac12}$$+$$\color{green}{\frac12+ \frac12+ \frac12}$$=\frac18+ \frac18$$=\frac14$

Odpowiedź: Prawdopodobieństwo zdarzenia $A$ w trzykrotnym rzucie monetą wynosi $P(A)= \frac14$.

A. W rozwiązaniu tego typu zadania pomoże nam metoda drzewa. Skonstruujmy drzewo stochastyczne ilustrujące przebieg doświadczenia losowego opisanego w poleceniu.
Zacznijmy od początku drzewa.
Wierzchołki drzewa po pierwszym ruchu będą opisane kolejnymi liczbami na kostce. Poszczególne zdarzenia zachodzą z prawdopodobieństwem $\frac16$. Jeżeli wylosujemy liczbę parzystą rzucamy monetą.

Zdarzenia {$O$} lub {$R$} zachodzą z prawdopodobieństwem $\frac12$. Jeżeli wylosujemy liczbę nieparzystą zakładamy że wypadnie orzeł $O$- jest to zdarzenie pewne które zachodzi z prawdopodobieństwem $1$. $\color{red}{Kolorem}$ oznaczone są wszystkie gałęzie opisujące zdarzenie losowe $A$ czyli wylosowanie reszki.

Z reguły sum mamy, że $P(A)=$$\color{blue}{\frac16 \cdot \frac12}$$+$$\color{green}{\frac16 \cdot \frac12}$$+$$\color{yellow}{\frac16 \cdot \frac12}$$=\frac1{12} + \frac1{12} + \frac1{12}$$=\frac3{12}=\frac14$

Odpowiedź: Prawdopodobieństwo wylosowania reszki wynosi $P(A)=\frac14$.

B. Drzewo stochastyczne jest skonstruowane podobnie jak w przykładzie $A$.
Zmienią się jedynie gałęzie oznaczające zdarzenie losowe $B-$ wylosowanie orła.

Z reguły sum mamy, że $P(B)=\frac16 \cdot 1$$ + \frac16 \cdot \frac12$$ + \frac16 \cdot 1 + \frac16 \cdot \frac12$$ + \frac16 \cdot 1$$ + \frac16 \cdot \frac12$$=\frac9{12}$$=\frac34$.

Zauważmy, że wylosowanie orła jest zdarzeniem przeciwnym do wylosowania reszki zatem $P(B)=P(A’)$.

Wiemy, że $P(A)=\frac14$ oraz $P(A’)=1-P(A)$.

$P(A’)=1- \frac14$

$P(A’)=\frac34$ czyli $P(B)=\frac34$

Odpowiedź: Prawdopodobieństwo wylosowania orła wynosi $P(B)=\frac34$.

W rozwiązaniu tego typu zadania pomoże nam metoda drzewa. Skonstruujmy drzewo stochastyczne ilustrujące przebieg doświadczenia losowego opisanego w poleceniu.

$1°$ Jak opisać drzewo po pierwszym rzucie?

Wierzchołki drzewa po pierwszym ruchu będą opisane $o,b$, gdzie $B$ oznacza wylosowanie kuli białej
i $C$ oznacza wylosowanie kuli czarnej.

Naszym zbiorem $Ω$ jest zbiór kul. Mamy 7 kul białych i 5 kul czarnych- w sumie 12 kul $\Rightarrow$ $|Ω|=12$ w pierwszym rzucie.

Prawdopodobieństwo wylosowania kuli białej wynosi $\frac7{12}$.

Prawdopodobieństwo wylosowania kuli czarnej wynosi $\frac5{12}$.

$2°$ Jak opisać drzewo po drugim rzucie?

Naszym zbiorem $Ω$ jest zbiór kul po pierwszym losowaniu. Losujemy bez zwrotu,
więc nie dostajemy z powrotem kuli do naszej puli równej 12.
Wynika z tego, że możemy losować tylko z 12-1 kul $\Rightarrow$ $|Ω|=11$

W zależności od pierwszego ruchu zmienimy pulę kul w odpowiednim kolorze:

• Jeżeli w pierwszym rzucie wylosujemy kulę białą $B$ to prawdopodobieństwo wylosowania kuli białej w drugim rzucie wyniesie $\frac{7-1}{11}=\frac6{11}$ a prawdopodobieństwo wylosowania kuli czarnej $C$
  w drugim rzucie wyniesie $\frac5{11}$
• Jeżeli w pierwszym rzucie wylosujemy kulę czarną $C$ to prawdopodobieństwo wylosowania kuli czarnej w drugim rzucie wyniesie $\frac{5-1}{11}=\frac4{11}$ a prawdopodobieństwo wylosowania kuli białej $B$
  w drugim rzucie wyniesie $\frac7{11}$

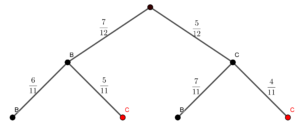$\color{red}{Kolorem}$ oznaczone są wszystkie gałęzie opisujące zdarzenie losowe $A$ czyli wylosowanie kuli czarnej za drugim razem.

Z reguły sum mamy, że:
$P(A)=\frac7{12} \cdot \frac5{11} + \frac5{12} \cdot \frac4{11}=$$\frac{35}{132} + \frac{20}{132}=$$\frac{55}{132}$.

Odpowiedź: Prawdopodobieństwo, że za drugim razem wylosujemy kulę czarną wynosi $\frac{55}{132}$.