Funkcją liniową nazywamy funkcję $f$ określoną wzorem:
$$\Large{y={\color[rgb]{0.9, 0.0, 0.45}a} \cdot x + {\color[rgb]{0.2, 0.2, 0.6}b}}$$gdzie ${\color[rgb]{0.9, 0.0, 0.45}a}$, ${\color[rgb]{0.2, 0.2, 0.6}b}$ $\in\mathbb{R}$ oraz
$$\Large{y={\color[rgb]{0.9, 0.0, 0.45}a} \cdot x + {\color[rgb]{0.2, 0.2, 0.6}b}}$$gdzie ${\color[rgb]{0.9, 0.0, 0.45}a}$, ${\color[rgb]{0.2, 0.2, 0.6}b}$ $\in\mathbb{R}$ oraz
- ${\color[rgb]{0.9, 0.0, 0.45}a}$ nazywamy ${\color[rgb]{0.9, 0.0, 0.45}współczynnikiem}$ ${\color[rgb]{0.9, 0.0, 0.45}kierunkowym}$ ${\color[rgb]{0.9, 0.0, 0.45} prostej}$
- ${\color[rgb]{0.2, 0.2, 0.6}b}$ nazywamy ${\color[rgb]{0.2, 0.2, 0.6}wyrazem}$ ${\color[rgb]{0.2, 0.2, 0.6}wolnym}$
Uwaga: Możemy spotkać się z takim zapisem:
- $y={\color[rgb]{0.9, 0.0, 0.45}a} \cdot x + {\color[rgb]{0.2, 0.2, 0.6}b}$ i jest to równanie kierunkowe prostej
- $Ax + By + C=0$ i jest to równanie ogólne prostej, gdzie $A^2 +B^2 \neq 0$ tj. współczynniki $A$ i $B$ nie są równocześnie równe $0$
Co możemy odczytać z postaci $y=a \cdot x + b$ ?
1) Liczba ${\color[rgb]{0.9, 0.0, 0.45}a}$ to współczynnik kierunkowy prostej
- $a=tg \alpha$ [odnośnik do trygonometrii]
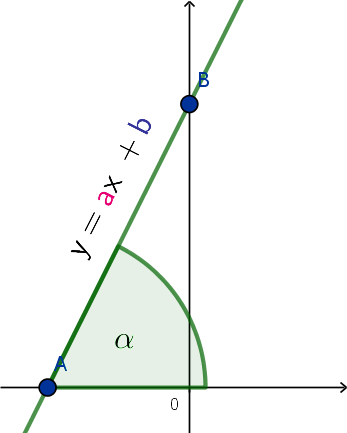
2) Punkt $B=(0, {\color[rgb]{0.2, 0.2, 0.6}b})$ to punkt przecięcia wykresu funkcji liniowej z osią $OY$
3) Miejsce zerowe funkcji liniowej obliczymy ze wzoru $x_0=\frac{-{\color[rgb]{0.2, 0.2, 0.6}b}}{\color[rgb]{0.9, 0.0, 0.45}a}$ $\Leftrightarrow$ Prosta przecina oś $OX$ w punkcie $A=(x_0,0)$
4) Funkcja liniowa jest
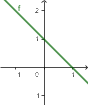
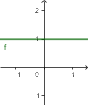
| malejąca | stała | rosnąca |
 |
 |
 |
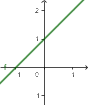| ${\color[rgb]{0.9, 0.0, 0.45}a}<0$ | ${\color[rgb]{0.9, 0.0, 0.45}a}=0$ | ${\color[rgb]{0.9, 0.0, 0.45}a}>0$ |
Przykłady
Przykład: W punkcie o jakich współrzędnych wykres funkcji liniowej $y=3x-5$ przecina oś $OY$?
Równanie kierunkowe prostej ma ogólną postać $y={\color[rgb]{0.9, 0.0, 0.45}a} \cdot x {\color[rgb]{0.2, 0.2, 0.6}b}$. W naszym zadaniu $y={\color[rgb]{0.9, 0.0, 0.45}3} \cdot x + ({\color[rgb]{0.2, 0.2, 0.6}-5})$
Zatem
${\color[rgb]{0.9, 0.0, 0.45}a}={\color[rgb]{0.9, 0.0, 0.45}3}$ i ${\color[rgb]{0.2, 0.2, 0.6}b}={\color[rgb]{0.2, 0.2, 0.6}-5}$
Zatem
${\color[rgb]{0.9, 0.0, 0.45}a}={\color[rgb]{0.9, 0.0, 0.45}3}$ i ${\color[rgb]{0.2, 0.2, 0.6}b}={\color[rgb]{0.2, 0.2, 0.6}-5}$
Punkt $B=(0, {\color[rgb]{0.2, 0.2, 0.6}b})$ to punkt przecięcia wykresu funkcji liniowej z osią $OY$, czyli szukany punkt ma współrzędne $(0, {\color[rgb]{0.2, 0.2, 0.6}-5})$
Odpowiedź: Wykres funkcji liniowej $y=3x-5$ przecina oś $OY$ w punkcie $(0, -5)$.
Przykład: Określ, czy dana funkcja jest rosnąca/malejąca/stała oraz znajdź współrzędne punktu przecięcia prostej z osią $OX$.
A. $y=2x+1$
B. $y=-\frac12x+2$
C. $y=\frac13x$
D. $y=1$
| Funkcja jest | Punkt przecięcia z osią $OY$ | |||||
| A. | $y={\color[rgb]{0.9, 0.0, 0.45}2}x+{\color[rgb]{0.2, 0.2, 0.6}1}$ | ${\color[rgb]{0.9, 0.0, 0.45}a}{\color[rgb]{0.1, 0.1, 0.1}=}{\color[rgb]{0.9, 0.0, 0.45}2}$ | ${\color[rgb]{0.9, 0.0, 0.45}a}>0$ | rosnąca | ${\color[rgb]{0.2, 0.2, 0.6}b}={\color[rgb]{0.2, 0.2, 0.6}1}$ | $(0, {\color[rgb]{0.2, 0.2, 0.6}1})$ |
| B. | $y={\color[rgb]{0.9, 0.0, 0.45}-\frac12}x+{\color[rgb]{0.2, 0.2, 0.6}2}$ | ${\color[rgb]{0.9, 0.0, 0.45}a}{\color[rgb]{0.1, 0.1, 0.1}=}{\color[rgb]{0.9, 0.0, 0.45}-\frac12}$ | ${\color[rgb]{0.9, 0.0, 0.45}a}<0$ | malejąca | ${\color[rgb]{0.2, 0.2, 0.6}b}={\color[rgb]{0.2, 0.2, 0.6}2}$ | $(0, {\color[rgb]{0.2, 0.2, 0.6}2})$ |
| C. | $y={\color[rgb]{0.9, 0.0, 0.45}\frac13}x$ | ${\color[rgb]{0.9, 0.0, 0.45}a}{\color[rgb]{0.1, 0.1, 0.1}=}{\color[rgb]{0.9, 0.0, 0.45}\frac13}$ | ${\color[rgb]{0.9, 0.0, 0.45}a}>0$ | rosnąca | ${\color[rgb]{0.2, 0.2, 0.6}b}={\color[rgb]{0.2, 0.2, 0.6}0}$ | $(0, {\color[rgb]{0.2, 0.2, 0.6}0})$ |
| D. | $y={\color[rgb]{0.2, 0.2, 0.6}1}$ | ${\color[rgb]{0.9, 0.0, 0.45}a}{\color[rgb]{0.1, 0.1, 0.1}=}{\color[rgb]{0.9, 0.0, 0.45}0}$ | ${\color[rgb]{0.9, 0.0, 0.45}a}=0$ | stała | ${\color[rgb]{0.2, 0.2, 0.6}b}={\color[rgb]{0.2, 0.2, 0.6}1}$ | $(0, {\color[rgb]{0.2, 0.2, 0.6}1})$ |
Przykład: Dana jest funkcja liniowa określona wzorem $f(x)=(\frac13m – 2)x +7$. Wiedząc, że należy do niej punkt $A=(1,4)$ znajdź $m$.
Punkt $A=({\color[rgb]{1.0, 0.6, 0.0}1},{\color[rgb]{0.0, 0.7, 0.0}4})$ należy do podanej funkcji. Wiemy więc, że:
$f({\color[rgb]{1.0, 0.6, 0.0}x})={\color[rgb]{0.0, 0.7, 0.0}y}$ $\Leftrightarrow$ $f({\color[rgb]{1.0, 0.6, 0.0}1})={\color[rgb]{0.0, 0.7, 0.0}4}$
Mamy że:
$f({\color[rgb]{1.0, 0.6, 0.0}x})={\color[rgb]{0.0, 0.7, 0.0}y}$ $\Leftrightarrow$ $f({\color[rgb]{1.0, 0.6, 0.0}1})={\color[rgb]{0.0, 0.7, 0.0}4}$
Mamy że:
| $f(x)=(\frac13m – 2)x +7$ | |
| ${\color[rgb]{0.0, 0.7, 0.0}4}=(\frac13m – 2)$ $\cdot$ ${\color[rgb]{1.0, 0.6, 0.0}1} +7$ | |
| $4=\frac13m – 2 +7$ | |
| $4=\frac13m +5$ | $|-\frac13m$ |
| $-\frac13m +4=5$ | $|-4$ |
| $-\frac13m=1$ | $|:(-\frac13)$ |
| $m=-3$ |
Odpowiedź: $m=-3$.
Przykład: Prosta o równaniu $y=2x+(3m-6)$ przechodzi przez punkt $A=(1,2)$. Wyznacz niewiadomą $m$.
Podstawmy współrzędne punktu $A=({\color[rgb]{1.0, 0.6, 0.0}1},{\color[rgb]{0.0, 0.7, 0.0}2})$ do równania funkcji $y=2x+(3m-6)$.
| ${\color[rgb]{0.0, 0.7, 0.0}y}=2{\color[rgb]{1.0, 0.6, 0.0}x}+(3m-6)$ | Podstawmy punkt $A=({\color[rgb]{1.0, 0.6, 0.0}1},{\color[rgb]{0.0, 0.7, 0.0}2})$ |
| ${\color[rgb]{0.0, 0.7, 0.0}2}=2 \cdot {\color[rgb]{1.0, 0.6, 0.0}1}+(3m-6)$ | |
| $2=2+3m-6$ | $|-3m$ |
| $-3m+2=2-6$ | |
| $-3m+2=-4$ | $|-2$ |
| $-3m=-6$ | $|:(-3)$ |
| $m=2$ |
Odpowiedź: $m=2$.
Co możemy odczytać z równania ogólnego prostej $Ax + By + C=0$ ?
| Jeżeli | $A=0$ | to prosta | jest równoległa do osi OX |  |
| $B=0$ | jest równoległa do osi OY |  |
||
| $C=0$ | przechodzi przez początek układu współrzędnych czyli punkt $(0, 0)$ |
 |
Uwaga: Tego nie musisz wkuwać! Wybrane wzory matematyczne – CKE strona 5.
0
2 responses to “Wzór funkcji liniowej”