Wartości funkcji trygonometrycznych dla kątów $0°$, $30°$, $45°$, $60°$, $90°$ wynoszą:
| $α$ | $0°$ | $30°$ | $45°$ | $60°$ | $90°$ |
| $sinα$ | $0$ | $\frac 12$ | $\frac{\sqrt2}{2}$ | $\frac{\sqrt3}{2}$ | $1$ |
| $cosα$ | $1$ | $\frac{\sqrt3}{2}$ | $\frac{\sqrt2}{2}$ | $\frac 12$ | $0$ |
| $tgα$ | $0$ | $\frac{\sqrt3}{3}$ | $1$ | $\sqrt{3}$ | $1$ |
| $ctgα$ | nie
istnieje |
$\sqrt{3}$ | $1$ | $\frac{\sqrt3}{3}$ |
nie istnieje |
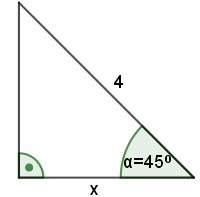
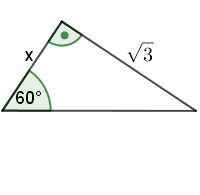
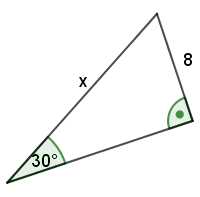
Przykład: Oblicz długość boku $x$.
Przykład: Oblicz pole i obwód trapezu równoramiennego, którego krótsza podstawa ma długość $4$, a ramię długości $6$ tworzy z dłuższą podstawą kąt $30°$.
Zaznaczamy dane na rysunku:
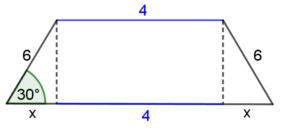
Musimy znaleźć długość odcinków $x$ oraz wysokości $h$. Możemy “wyjąć” trójkąt z trapeza.
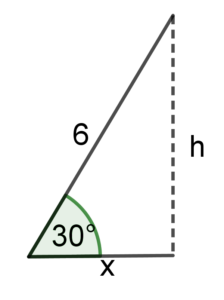
Korzystając z tego, że $sin30° = \frac 12$ obliczamy
$sin30° = \frac{h}{6}$
$\frac 12 = \frac h6$
Wymnażamy “na krzyż”
$2h = 6$
$h = 3$
Na tym etapie $x$ możesz wyliczyć z twierdzenia Pitagorasa lub wiedząc, że
$cos30° = \frac{x}{6}$
$\frac{\sqrt{3}}{2} = \frac{x}{6}$
Wymnażamy “na krzyż”
$2x = 6\sqrt{3}$
$x = 3\sqrt{3}$
Obliczamy pole i obwód trapezu:
- wysokość: $h = 3$
- długość krótszej podstawy: $a = 4$
- długość dłuższej podstawy: $b = 4 + 2x$$ = 4 + 2\sqrt{3}$$ = 4 + 6\sqrt{3}$
- długość ramienia: $c = 6$
$P = \frac 12 \cdot (a + b) \cdot h $$ = \frac 12 \cdot (4 + 4 + 6\sqrt{3}) \cdot 3$$ = \frac{3}{2}\cdot(8+6\sqrt{3})=\frac{24+18\sqrt{3}}{2}$$ = 12 + 9\sqrt{3}$
Obwód trapezu:
$L = a + b + 2\cdot c$$ = 4 + 4 + 6\sqrt{3} + 2 \cdot 6$$ = 8 + 6 \sqrt{3} + 12$$ = 20 + 6\sqrt{3}$
Przykład: Przekątna prostokąta ma długość $4$ i tworzy z dłuższym bokiem kąt $60°$. Oblicz obwód i pole prostokąta.

Z sinusa i cosinusa wyliczamy brakujące długości:
$sin60° = \frac{b}{4}$
$\frac{\sqrt{3}}{2} = \frac {b}{4}$
$4\sqrt 3 = 2b$
$b = 2\sqrt{3}$
$cos60° = \frac{a}{4}$
$\frac 12 = \frac{a}{4}$
$2a = 4$
$a = 2$
(Tu ponownie można zastosować twierdzenia Pitagorasa znając już jeden bok.)
$P = a \cdot b$$ = 2 \cdot 2\sqrt{3}$$ = 4\sqrt{3}$
$L = 2a + 2b$$ = 2 \cdot 2 + 2 \cdot 2\sqrt{3}$$ = 4 + 4\sqrt{3}$
Odpowiedź: Pole prostokąta wynosi $ 4\sqrt{3}$, zaś obwód $ 4 + 4\sqrt{3}$.
Przykład: Obwód trójkąta, przedstawionego na rysunku, jest równy:
a) $(3 + \frac{\sqrt{3}}{2})a$
b) $(2 + \frac{\sqrt{2}}{2})a$
c) $(3 + \sqrt{3})a$
d) $(2 + \sqrt{2})a$

Musimy uzależnić długości ΙABΙ i ΙACΙ względem $a$. Z sinusa wyliczamy ΙACΙ:
$sin30° = \frac{a}{\left|AC\right|}$
$\frac 12 = \frac{a}{\left|AC\right|}$
$\left|AC\right| = 2a$
Z cosinusa wyznaczamy ΙABΙ:
$cos30° = \frac{\left|AB\right|}{\left|AC\right|}$
$\frac{\sqrt{3}}{2} = \frac{\left|AB\right|}{\left|AC\right|}$
$2\sqrt{3}a = 2\left|AB\right|\hspace{0,5cm}|: 2$
$\left|AB\right| = \sqrt{3}a$
Otrzymujemy obwód:
$L = a + \sqrt{3}a + 2a$$ = 3a + \sqrt{3}a$
Wyciągamy $a$ przed nawias: $L = a(3 + \sqrt{3})$
Odpowiedź: Obwód tego trójkąta wynosi $L = a(3 + \sqrt{3})$ – zatem odpowiedź c).
