Wierzchołek funkcji kwadratowej – wzór na współrzędne wierzchołka paraboli
Wykresem funkcji kwadratowej jest parabola o wierzchołku oznaczonym punktem $W = (p, q)$.
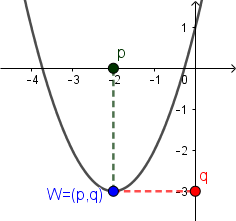
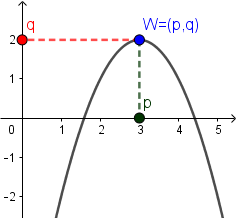
Wierzchołek funkcji kwadratowej dla funkcji postaci $f(x) = ax^2 + bx + c$ dany jest wzorami:
$$\Large{p = – \frac{b}{2a}, q = – \frac{\Delta}{4a}}$$
gdzie $\Delta = b^2 – 4ac$, czyli
$$\Large{W = ( – \frac{b}{2a}, – \frac{\Delta}{4a})}$$
Współrzędne wierzchołka będą potrzebne do wyznaczania zbioru wartości funkcji czy jej przedziałów monotoniczności.
Przykład: Wyznacz współrzędne wierzchołka dla funkcji $f(x)=2x^2+6x-2$.
Odczytujemy współrzędne $a,b,c$, mamy: $a=2$, $b=6$, $c=-2$.
Obliczamy deltę:
$\Delta=6^2-4 \cdot 2 \cdot (-2)$$=36-(-16)$$=36+16=52$
Podstawiamy nasze dane do wzoru na $p$ i $q$:
$p=\frac{-b}{2a}$$=\frac{-6}{2 \cdot 2}$$=\frac{-6}{4}$$=\frac{-3}{2}$$=-1,5$
$q=\frac{-\Delta}{4a}$$=\frac{-52}{4 \cdot 2}$$=\frac{-52}{8}$$=-6,5$
Odpowiedź: Wierzchołek jest w punkcie $W=(-1,5, -6,5)$.
Wierzchołek funkcji a jej postać kanoniczna
Z tej postaci od razu możemy wprost odczytać współrzędne wierzchołka $p$, $q$.
Przykład: Dana jest funkcja $f(x) = 3(x – 5)^2 + 4$. Wyznacz współrzędne wierzchołka.
Widzimy, że jest to wzór funkcji kwadratowej w postaci kanonicznej. Zatem porównując wzór naszej funkcji ze wzorem $f(x) = a(x – p)^2 +q$ odczytujemy, że $p = 5$ i $q = 4$.
Odpowiedź: Wierzchołek paraboli tej funkcji jest w punkcie $W = (5, 4)$.
Przykład: Wyznacz wierzchołek funkcji.
a) $f(x)=(x-2)^2+1$
b) $f(x)=2(x+1)^2$
c) $f(x)=x^2-2$
d) $f(x)=2x^2$
a) $W=(2, 1)$
b) $W=(-1, 0)$
c) Możemy to funkcję zapisać $f(x)=(x-0)^2-2$. Stąd $W=(0, -2)$.
d) Podobnie jak wyżej możemy to rozpisać: $f(x)=2(x-0)^2+0$, stąd $W=(0, 0)$.
Przykład : (CKE) Dana jest parabola o równaniu $y=x^2+8x-14$. Pierwsza współrzędna wierzchołka tej paraboli jest równa:
A. $x=-8$ $\qquad$ B. $x=-4$ $\qquad$ C. $x=4$ $\qquad$ D. $x=8$
Mamy dane: $a=1$, $b=8$, $c=-14$.
Obliczamy pierwszą współrzędna wierzchołka:
$p=\frac{-8}{2 \cdot 1}$$=\frac{-8}{2}=-4$
Odpowiedź: Pierwsza współrzędna wierzchołka jest równa $-4$ – odpowiedź B..
Przykład: Wyznacz współrzędne wierzchołka paraboli o równaniu $f(x) = 2(x – 1)(x + 3)$.
Z takiej postaci funkcji wprost odczytujemy jej miejsca zerowe: $x_1 = 1$ i $x_2 = -3$.
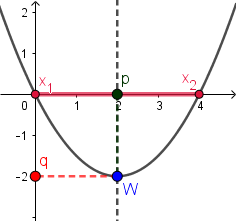
Zgodnie z uwagą:$p = \frac{x_1 + x_2}{2}$$ = \frac{1 + (-3)}{2}$$ = \frac{-2}{2} = -1$Wartość funkcji dla $p = -1$ obliczamy stosując jej wzór:$q = f(p) = f(-1)$$ = 2(- 1 – 1)(-1 + 3)$$ = 2 \cdot (- 2)\cdot 2$$ = – 8$
Odpowiedź: Współrzędne wierzchołka to $W = ( -1, -8)$.
Przykład: Dla danej funkcji $f(x)=-x^2+2x-7$ wyznacz zbiór wartości.
Aby wyznaczyć zbiór wartości policzymy wierzchołek. Mamy dane:
$a=-1$, $b=2$, $c=-7$.
Obliczamy deltę:
$\Delta=2^2-4 \cdot (-1) \cdot (-7)$$=4-28$$=-24$
Wyznaczamy wierzchołek:
$p=\frac{-2}{2 \cdot (-1)}$$=\frac{-2}{-2}$$=1$
$q=\frac{-(-24)}{4 \cdot (-1)}$$=\frac{24}{-4}$$=-6$
$W=(1,-6)$
Rysujemy poglądowy wykres funkcji.
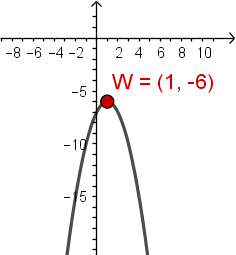
Odczytujemy, że $Z_w=(-\infty,-6>$.
