Prostopadłościan
Prostopadłościanem nazywamy taki graniastosłup, którego wszystkie ściany są prostokątami.
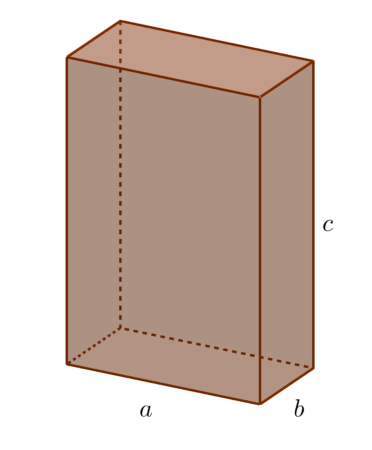
Boki $a,b,c$ nazywamy krawędziami prostopadłościanu.

Boki $a,b,c$ nazywamy krawędziami prostopadłościanu.
Prostopadłościan ma zawsze:
- 6 ścian
- 12 krawędzi
- 8 wierzchołków
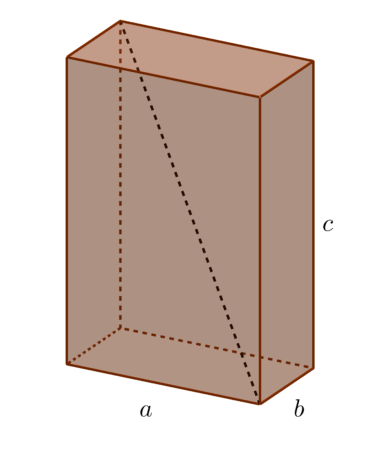
Przekątną prostopadłościanu nazywamy odcinek łączący dwa jego przeciwległe wierzchołki.

Objętość prostopadłościanu
Objętość prostopadłościanu opisuje wzór:
$$V=a\cdot b\cdot c$$
gdzie $a,b,c$ to długości krawędzi prostopadłościanu.
$$V=a\cdot b\cdot c$$
gdzie $a,b,c$ to długości krawędzi prostopadłościanu.
Pole powierzchni całkowitej prostopadłościanu
$Pole\: powierzchni\: całkowitej=Pole\: powierzchni\: bocznej+2\cdot Pole\: podstawy$
$Pole\: powierzchni\: bocznej=ac+ac+bc+bc=2 \cdot ac+2\cdot bc$
$Pole\: podstawy=ab$
tzn.
Pole powierzchni całkowitej prostopadłościanu opisuje wzór:
$$P_{C}=2(ab+bc+ac)$$
gdzie $a,b,c$ to długości krawędzi prostopadłościanu.
$$P_{C}=2(ab+bc+ac)$$
gdzie $a,b,c$ to długości krawędzi prostopadłościanu.
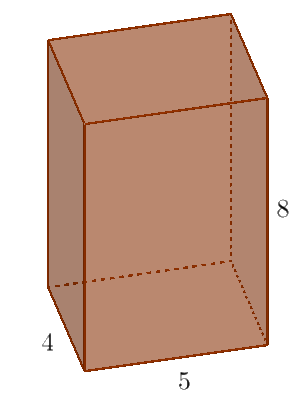
Przykład 1: Dany jest prostopadłościan o bokach długości $a=4,\: b=5,$ oraz $c=8.$ Oblicz pole powierzchni całkowitej i objętość tego prostopadłościanu.
Narysujmy obrazek poglądowy:
Ze wzoru na pole powierzchni całkowitej prostopadłościanu mamy:

Ze wzoru na pole powierzchni całkowitej prostopadłościanu mamy:
$P_{C}=2(ab+bc+ac)=2(4\cdot 5+5\cdot 8+4\cdot 8)=2(20+40+32)=2\cdot 92=184$
Ze wzoru na objętość prostopadłościanu otrzymujemy:
$V=abc=4\cdot 5\cdot 8=160$
Odpowiedź: Pole powierzchni całkowitej tego prostopadłościanu to 184, a jego objętość, to 160.
Przykład 2:Przekątna prostopadłościanu ma długość $2\sqrt{26}.$ Długość ścian jego podstawy wynoszą odpowiednio 6 i 8. Oblicz objętość tego prostopadłościanu.
Zacznijmy od narysowania rysunku poglądowego:
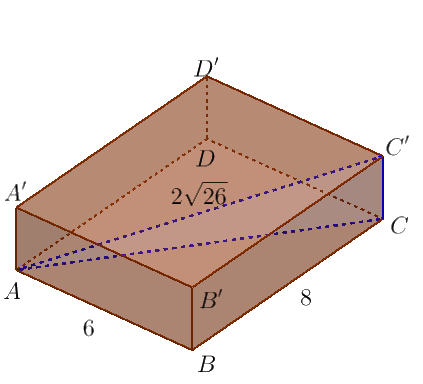
Aby obliczyć objętość prostopadłościanu potrzebujemy znać wysokość naszej bryły. Wyliczymy ją wykorzystując dwukrotnie twierdzenie Pitagorasa, najpierw do trójkąta $ABC,$ następnie do trójkąta $ACC^{\prime}.$
Zacznijmy od narysowania trójkąta $ABC:$

Z twierdzenia Pitagorasa wyznaczmy $\mid AC\mid .$
$\mid AB \mid ^2 + \mid BC \mid ^2=\mid AC \mid ^2$
$6^2+8^2=\mid AC \mid ^2$
$\mid AC \mid ^2=36+64$
$\mid AC \mid ^2=100$
$\mid AC \mid =10 \quad \vee \quad \mid AC \mid =-10$
Ponieważ odległość musi być nieujemna, to: $\mid AC \mid =10.$
Teraz z obliczonym $\mid AC\mid$ narysujmy trójkąt $ACC^{\prime}.$

Ponownie korzystając z twierdzenia Pitagorasa obliczymy interesującą nas długość $\mid CC^{\prime}\mid .$
$\mid AC \mid ^2 + \mid CC^{\prime} \mid ^2=\mid AC^{\prime} \mid ^2$
$10^2+\mid CC^{\prime} \mid ^2=(2\sqrt{26})^2$
$\mid CC^{\prime} \mid ^2=(2\sqrt{26})^2-10^2$
$\mid CC^{\prime} \mid ^2=104-100$
$\mid CC^{\prime} \mid ^2=4$
$\mid CC^{\prime} \mid =2 \quad \vee \quad \mid CC^{\prime} \mid =-2 $
Ponieważ odległość musi być nieujemna, to: $\mid CC^{\prime} \mid =2.$
Pozostało nam jedynie obliczyć objętość przedstawionego prostopadłościanu podstawiając do wzoru:
$V=\mid AB\mid \cdot \mid BC\mid \cdot \mid CC^{\prime}\mid = 6\cdot 8\cdot 2=96.$
Odpowiedź: Objętość tego prostopadłościanu, to 96.

Aby obliczyć objętość prostopadłościanu potrzebujemy znać wysokość naszej bryły. Wyliczymy ją wykorzystując dwukrotnie twierdzenie Pitagorasa, najpierw do trójkąta $ABC,$ następnie do trójkąta $ACC^{\prime}.$
Zacznijmy od narysowania trójkąta $ABC:$
Z twierdzenia Pitagorasa wyznaczmy $\mid AC\mid .$
$\mid AB \mid ^2 + \mid BC \mid ^2=\mid AC \mid ^2$
$6^2+8^2=\mid AC \mid ^2$
$\mid AC \mid ^2=36+64$
$\mid AC \mid ^2=100$
$\mid AC \mid =10 \quad \vee \quad \mid AC \mid =-10$
Ponieważ odległość musi być nieujemna, to: $\mid AC \mid =10.$
Teraz z obliczonym $\mid AC\mid$ narysujmy trójkąt $ACC^{\prime}.$
Ponownie korzystając z twierdzenia Pitagorasa obliczymy interesującą nas długość $\mid CC^{\prime}\mid .$
$\mid AC \mid ^2 + \mid CC^{\prime} \mid ^2=\mid AC^{\prime} \mid ^2$
$10^2+\mid CC^{\prime} \mid ^2=(2\sqrt{26})^2$
$\mid CC^{\prime} \mid ^2=(2\sqrt{26})^2-10^2$
$\mid CC^{\prime} \mid ^2=104-100$
$\mid CC^{\prime} \mid ^2=4$
$\mid CC^{\prime} \mid =2 \quad \vee \quad \mid CC^{\prime} \mid =-2 $
Ponieważ odległość musi być nieujemna, to: $\mid CC^{\prime} \mid =2.$
Pozostało nam jedynie obliczyć objętość przedstawionego prostopadłościanu podstawiając do wzoru:
$V=\mid AB\mid \cdot \mid BC\mid \cdot \mid CC^{\prime}\mid = 6\cdot 8\cdot 2=96.$
Odpowiedź: Objętość tego prostopadłościanu, to 96.
Przykład 3: Przekątna podstawy prostopadłościanu ma długość 5. Dłuższy bok podstawy ma długość 4, a wysokość bryły wynosi 2. Oblicz objętość prostopadłościanu i jego pole powierzchni bocznej.
Narysujmy obrazek poglądowy:
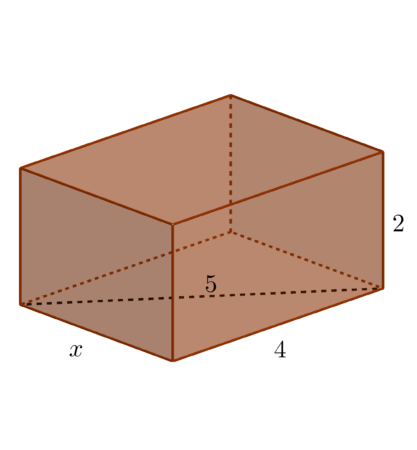
Do obliczenia objętości i pola powierzchni bocznej potrzebna nam będzie wartość $x,$ wyliczymy ją korzystając z twierdzenia Pitagorasa.
$x^2+4^2=5^2$
$x^2+16=25$
$x^2=9$
$x=3 \quad \vee \quad x=-3$
Ponieważ długość musi być nieujemna, to: $x=3.$
Po podstawieniu do wzoru na objętość prostopadłościanu otrzymujemy:
$V=3\cdot 4\cdot 2=24$
Powierzchnia boczna prostopadłościanu to cztery prostokąty, dwa z nich są wymiarów 3 na 2, a dwa pozostałe 4 na 2, zatem:
$P_{B}=2(3\cdot 2+ 4\cdot 2)=2\cdot 14=28$
Odpowiedź: Objętość podanego prostopadłościanu, to 24, a jego pole powierzchni bocznej, to 28.

Do obliczenia objętości i pola powierzchni bocznej potrzebna nam będzie wartość $x,$ wyliczymy ją korzystając z twierdzenia Pitagorasa.
$x^2+4^2=5^2$
$x^2+16=25$
$x^2=9$
$x=3 \quad \vee \quad x=-3$
Ponieważ długość musi być nieujemna, to: $x=3.$
Po podstawieniu do wzoru na objętość prostopadłościanu otrzymujemy:
$V=3\cdot 4\cdot 2=24$
Powierzchnia boczna prostopadłościanu to cztery prostokąty, dwa z nich są wymiarów 3 na 2, a dwa pozostałe 4 na 2, zatem:
$P_{B}=2(3\cdot 2+ 4\cdot 2)=2\cdot 14=28$
Odpowiedź: Objętość podanego prostopadłościanu, to 24, a jego pole powierzchni bocznej, to 28.
2+
