Przed rozwiązywaniem zadań przypomnij sobie działanie na zbiorach. [hiperłącze]

Przykład: Oblicz $P(A)$ wiedząc, że $P(A’)=3P(A)$.

Wiemy, że $P(A’)=1-P(A)$.
Mamy, że: $P(A’)=3P(A)$.
Podstawiamy:
$P(A’)=1-P(A)$
$3P(A)=1-P(A)\hspace{0,5cm}| +P(A)$
$4P(A)=1\hspace{0,5cm}| :4$
$P(A)=\frac14$
Odpowiedź: $P(A)=\frac14$.

Przykład: Zdarzenia $A$ i $B$ należą do $Ω$. Znajdź $P(A\cup B)$ i $P(A\cap B)$, jeżeli $P(A)=0,5$, $P(B)=0,3$ i $B\subset A$.

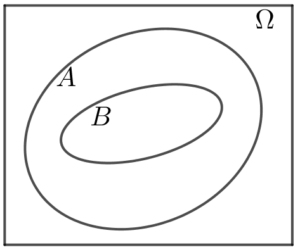
Naszkicujmy obrazek pokazujący wzajemne położenie zbiorów:

Widzimy, że $A\cup B=A$ i $A\cap B=B$.Mamy więc, że $P(A\cup B)=P(B)=0,3$.

$P(A\cap B)=P(A)=0,5$

Odpowiedź: $P(A\cup B)=0,3$ i $P(A\cap B)=0,5$.

Przykład: Zdarzenia losowe $A$ i $B$ są zawarte w przestrzeni $Ω$ Oblicz $P(B’)$ wiedząc, że $A\subset B$ oraz $P(A\cup B)=\frac7{10}$.

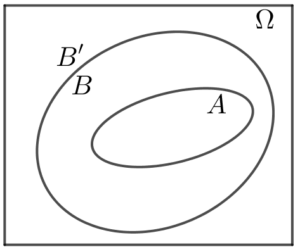
Naszkicujmy obrazek pokazujący wzajemne położenie zbiorów:

Skoro $A\subset B$ to $P(A\cup B)=P(B)$ $\Rightarrow$ $P(A\cup B)=\frac7{10}$.Zatem $P(B’)=1-P(B)$ i $P(B’)=1-\frac7{10}=\frac3{10}$.

Odpowiedź: $P(B’)=\frac3{10}$.

Przykład: O zdarzeniach losowych $A$ i $B$ wiemy, że $P(A)=\frac23$, $P(B)=\frac38$, $P(A\cup B)=\frac34$. Oblicz $P(A\cap B)$.

Wiemy, że $P(A\cup B)=P(A)+P(B)-P(A\cap B)$. Podstawmy znane wartości.

$$\frac34=\frac{25}{24}-P(A\cap B)\hspace{0,5cm}|+P(A\cap B)$$

$$\frac34+P(A\cap B)=\frac{25}{24}\hspace{0,5cm}|-\frac34$$

$$P(A\cap B)=\frac{25}{24}-\frac34=\frac{25}{24}-\frac{18}{24}$$

$$P(A\cap B)=\frac7{24}$$
Odpowiedź: $P(A\cap B)=\frac7{24}$.

Uwaga: Jeżeli $P(A\cap B)=0$ to zdarzenia $A$ i $B$ są rozłączne.

Przykład: Zdarzenia rozłączne $A$ i $B$ są zawarte w przestrzeni $Ω$. Oblicz prawdopodobieństwo sumy zdarzeń $A$ i $B$ wiedząc, że prawdopodobieństwo $A’$ jest dwa razy większe niż $A$ oraz prawdopodobieństwa $B$ i $B’$ są równe.

Wiemy, że $P(A\cup B)=P(A)+P(B)-P(A\cap B)$. Zdarzenia $A$ i $B$ są rozłączne, czyli $P(A\cap B)=P(\varnothing)=0$. Mamy, że $P(A\cup B)=P(A)+P(B)$.

Obliczmy $P(A)$.

Z treści zadania wiemy, że $2P(A)=P(A’)$.

Skorzystajmy ze wzoru $P(A’)=1-P(A)$. Mamy:
$$P(A’)=1-P(A)$$

$$2P(A)=1-P(A)\hspace{0,5cm}|+P(A)$$

$$3P(A)=1\hspace{0,5cm}|:3$$

$$P(A)=\frac13$$

Obliczmy $P(B)$.

$$P(B’)=1-P(B)$$

$$P(B)=1-P(B)\hspace{0,5cm}|+P(B)$$

$$2P(B)=1$$

$$P(B)=\frac12$$

Ostatecznie

$$P(A\cup B)=P(A)+P(B)=\frac13+\frac12=\frac56$$

Odpowiedź: Prawdopodobieństwo sumy rozłącznych zdarzeń $A$ i $B$ wynosi $\frac56$.

1+
Anita Księżak