1.Wysokość
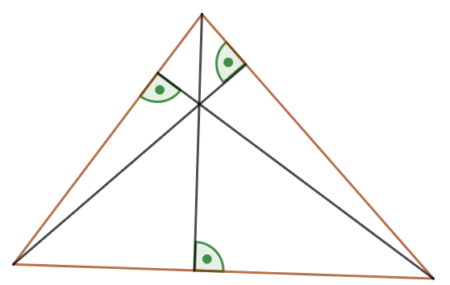
Wysokość trójkąta to najkrótszy odcinek łączący podstawę z przeciwległym wierzchołkiem. Oznacza to, że wysokość jest zawsze prostopadłą do podstawy (lub jej przedłużenia).
Każdy trójkąt ma trzy wysokości, które przecinają się w jednym punkcie (ortocentrum).
Przykład
Dany jest trójkąt równoboczny, którego pole jest równe $\ 6 \sqrt 3 $ bok tego trójkąta ma długość$\ 2 \sqrt 6 $.Oblicz jego wysokość
Dany jest trójkąt równoboczny, którego pole jest równe $\ 6 \sqrt 3 $ bok tego trójkąta ma długość$\ 2 \sqrt 6 $.Oblicz jego wysokość
Rozwiązanie
Rysunek pomocniczy
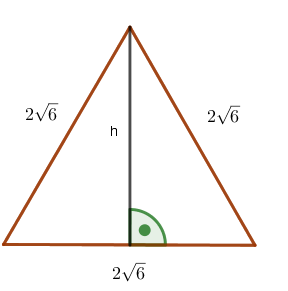
Wzór na pole trójkąta to: $\ P=\frac{1}{2} \cdot a \cdot h$
Podstawiając do wzoru nasze dane otrzymujemy równanie:
$$\ 6 \sqrt 3=\frac{1}{2} \cdot \ 2 \sqrt 6 \cdot h$$
Przekształcając otrzymujemy:
$$\ 6 \sqrt 3=\sqrt 6 \cdot h$$
$$\ 6 \frac{\sqrt 3}{\sqrt 6}=h$$
$$\ 3 \sqrt 2=h$$
Odpowiedź
Wysokość trójkąta wynosi $\ 3 \sqrt 2$
Rysunek pomocniczy

Wzór na pole trójkąta to: $\ P=\frac{1}{2} \cdot a \cdot h$
Podstawiając do wzoru nasze dane otrzymujemy równanie:
$$\ 6 \sqrt 3=\frac{1}{2} \cdot \ 2 \sqrt 6 \cdot h$$
Przekształcając otrzymujemy:
$$\ 6 \sqrt 3=\sqrt 6 \cdot h$$
$$\ 6 \frac{\sqrt 3}{\sqrt 6}=h$$
$$\ 3 \sqrt 2=h$$
Odpowiedź
Wysokość trójkąta wynosi $\ 3 \sqrt 2$
2.Środkowa
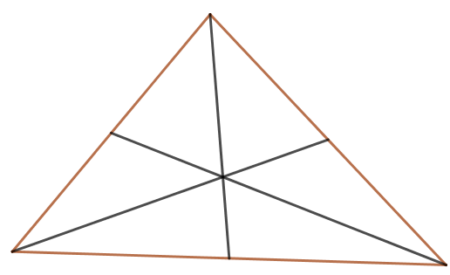
Środkowa trójkąta to odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku. Trójkąt ma trzy różne środkowe.
Środkowe przecinają się w jednym punkcie. Nazywamy go środkiem ciężkości trójkąta. Środek ciężkości dzieli każdą środkową w stosunku 2:1.
Przykład
W danym trójkącie ABC środkowa poprowadzona na najdłuższy bok ma długość 15 cm i dzieli ten trójkąt na dwa trójkąty z których jeden jest równoboczny a drugi równoramienny.Oblicz miary kątów danego trójkąta.
W danym trójkącie ABC środkowa poprowadzona na najdłuższy bok ma długość 15 cm i dzieli ten trójkąt na dwa trójkąty z których jeden jest równoboczny a drugi równoramienny.Oblicz miary kątów danego trójkąta.
Rozwiązanie
Rysunek pomocniczy
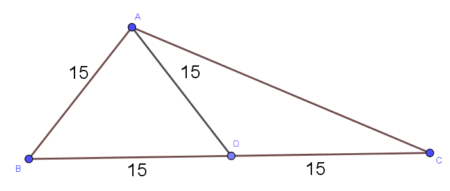
Trójkąt ABD jest równoboczny, więc każdy z jego kątów ma 60 stopni. Trójkąt ACD jest równoramienny zatem jego kąty przy podstawie są równe.
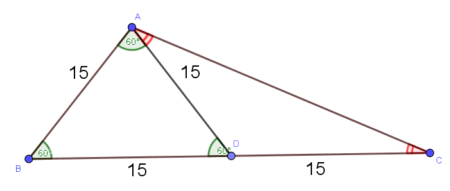
Skoro $|\sphericalangle ABD|=60^\circ$ oraz $|\sphericalangle BAD|=60^\circ$ to suma kątów $|\sphericalangle ACD|$ i $|\sphericalangle CAD|$ jest równa $60^\circ$
Rysunek pomocniczy

Trójkąt ABD jest równoboczny, więc każdy z jego kątów ma 60 stopni. Trójkąt ACD jest równoramienny zatem jego kąty przy podstawie są równe.

Skoro $|\sphericalangle ABD|=60^\circ$ oraz $|\sphericalangle BAD|=60^\circ$ to suma kątów $|\sphericalangle ACD|$ i $|\sphericalangle CAD|$ jest równa $60^\circ$
Z faktu, że trójkąt ACD jest równoramienny oznacza, że $|\sphericalangle ACD|=30^\circ$ i $|\sphericalangle CAD|=30^\circ$
Odpowiedź: Kąty w trójkącie wynoszą 60, 90 i 30 stopni.
3.Dwusieczna
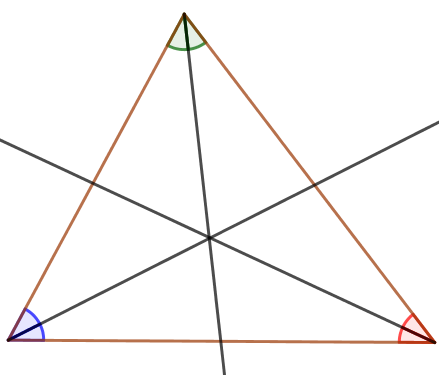
Dwusieczna kąta to półprosta dzieląca ten kąt na dwa równe kąty. Dwusieczne kątów trójkąta przecinają się w jednym punkcie
Twierdzenie o dwusiecznej
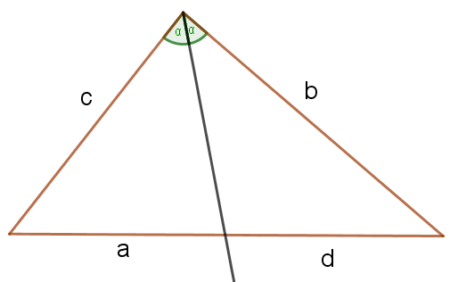
Dwusieczna dzieli bok trójkąta na odcinki a i d o długościach spełniających równianie:
$$\frac{a}{c}=\frac{d}{b}$$

Dwusieczna dzieli bok trójkąta na odcinki a i d o długościach spełniających równianie:
$$\frac{a}{c}=\frac{d}{b}$$
Przykład
Odcinek BD jest zawarty w dwusiecznej kąta ostrego ABC trójkąta prostokątnego, w którym przyprostokątne AC i BC mają długości odpowiednio 5 i 3 i kąt $\beta=29.5^\circ$.Oblicz miarę kąta $|\sphericalangle BAC|$.
Odcinek BD jest zawarty w dwusiecznej kąta ostrego ABC trójkąta prostokątnego, w którym przyprostokątne AC i BC mają długości odpowiednio 5 i 3 i kąt $\beta=29.5^\circ$.Oblicz miarę kąta $|\sphericalangle BAC|$.
Rozwiązanie
Rysunek pomocniczy
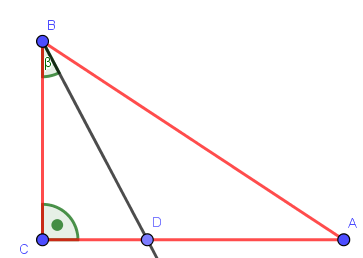
Odcinek BD jest zawarty w dwusiecznej kąta ostrego ABC.
Zatem kąt $\beta$ jest połową kąta $|\sphericalangle ABC|$
Czyli kąt $|\sphericalangle ABC|=2 \cdot 29.5^\circ=59^\circ$
Więc kąt $|\sphericalangle BAC|=180^\circ-90^\circ-59^\circ=31^\circ$
Odpowiedź: Kąt $|\sphericalangle BAC|$ wynosi $31^\circ$
Rysunek pomocniczy

Odcinek BD jest zawarty w dwusiecznej kąta ostrego ABC.
Zatem kąt $\beta$ jest połową kąta $|\sphericalangle ABC|$
Czyli kąt $|\sphericalangle ABC|=2 \cdot 29.5^\circ=59^\circ$
Więc kąt $|\sphericalangle BAC|=180^\circ-90^\circ-59^\circ=31^\circ$
Odpowiedź: Kąt $|\sphericalangle BAC|$ wynosi $31^\circ$
30+
