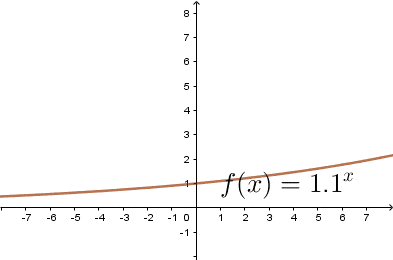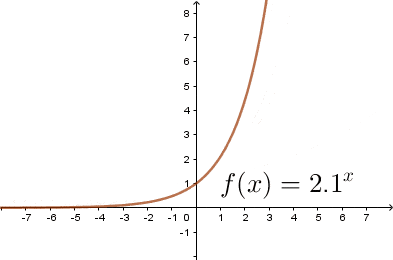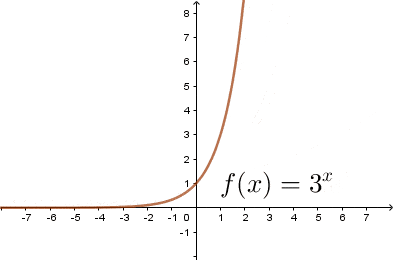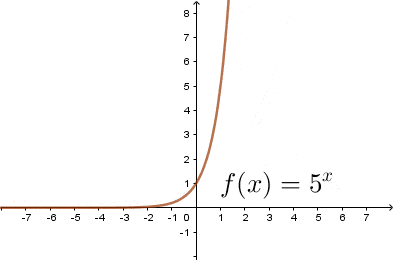Szkicowanie wykresu funkcji
Do narysowania wykresu funkcji wykorzystujemy znane nam jej własności, oraz liczymy jej wartości dla kilku wybranych przez nas argumentów, i umieszczamy je w tabelce. Przy rysunku wykonanym odręcznie im więcej punków umieścimy w tabelce, tym dokładniejszy będzie rysunek. Tutaj podamy kilka konkretnych przykładów funkcji, których wykres jest łatwo narysować.
Jak narysować wykres funkcji liniowej
Funkcja liniowa, czyli funkcja określona wzorem $$f(x)=ax+b,$$ gdzie
- a – współczynnik kierunkowy
- b – wyraz wolny
Jak wskazuje sama nazwa wykresem funkcji liniowej jest prosta.
Aby narysować wykres funkcji liniowej potrzebujemy znaleźć minimum dwa punkty należące do owego wykresy i przeprowadzić przez nie prostą.
- Gdy $a\neq 0$
Wtedy punkty, które znaleźć najłatwiej, to punkt przecięcia z osią $OY$, czyli punkt $(0,b)$ oraz inny dowolny punkt, który możemy wyliczyć podstawiając $x=1$ albo inną liczbę, dla której wartość funkcji wartość funkcji będzie łatwo policzyć. Ponadto warto wziąć jeden dodatkowy punkt, na wypadek pomyłki w obliczeniach.Przykład: Narysuj wykres funkcji $f(x)=2x-4.$W tym celu policzmy
$f(1)=2\cdot 1-4=-2$
oraz miejsce zerowe funkcji
$0=2x-4$
$2x=4$
$x=2$
Ponadto możemy odczytać punkt przecięcia z osią $OY$, ponieważ $b=-4$ będzie to punkt $(0,-4).$
Zatem nasze szukane punkty, to $(1,-2);(2,0);(0,-4).$$x$ $0$ $1$ $2$ $f(x)$ $-4$ $-2$ $0$ 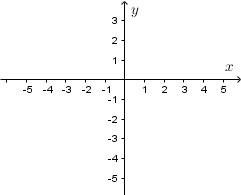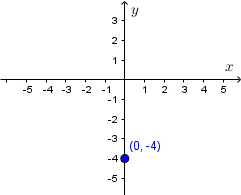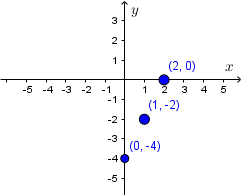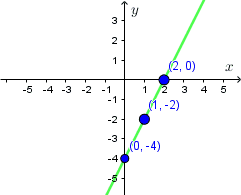 Zauważmy, że punktem, który można łatwo wyznaczyć, jest punkt przecięcia się wykresu funkcji z osią $OX.$ Faktycznie odczytując miejsce zerowe funkcji liniowej z jej postaci ogólnej mamy:
Zauważmy, że punktem, który można łatwo wyznaczyć, jest punkt przecięcia się wykresu funkcji z osią $OX.$ Faktycznie odczytując miejsce zerowe funkcji liniowej z jej postaci ogólnej mamy:
$0=ax+b$
$x=-\frac{b}{a}$
Zatem punk przecięcia się wykresy funkcji liniowej z osią $OX$ ma zawsze (dla $a\neq 0$) współrzędne $(-\frac{b}{a},0).$
Należy jednak pamiętać, że w przypadku, gdy $b=0$ punkt przecięcia się wykresu funkcji z osiami $OX$ oraz $OY$ pokryje się (będzie to punkt $(0,0)$) więc potrzebne będzie znalezienie kolejnego punktu. - Gdy $a=0$
Wtedy wykresem funkcji jest prosta równoległa do osi $OX$ przechodząca przez punkt $(0,b).$Przykład: Narysuj wykres funkcji $f(x)=3.$Odczytujemy, że $b=3,$ ponieważ $a=0,$ więc wykres funkcji jest prostą przechodzącą przez punkt $(0,3)$ równoległą do osi $OX,$ zatem:
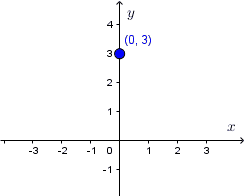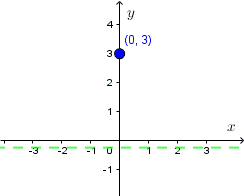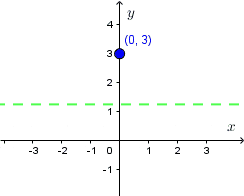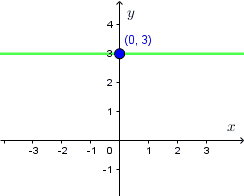
Jak narysować wykres funkcji kwadratowej
$$f(x)=ax^2+bx+c,$$
gdzie
- $a,b,c$ – stałe
- $a\neq 0$
Postać kanoniczna funkcji kwadratowej:
$$f(x)=a(x-p)^2+q,$$
gdzie
- $p=-\frac{b}{2a}$
- $q=-\frac{\Delta}{4a}$
- $\Delta=b^2-4ac$
Wykresem funkcji kwadratowej jest parabola o wierzchołku w punkcie $(p,q),$ oraz
- ramionach skierowanych „do góry”, gdy $a>0.$
- ramionach skierowanych „do dołu”, gdy $a<0.$
Aby narysować wykres funkcji kwadratowej potrzebujemy znaleźć co najmniej 3 punkty należące do wykresu funkcji, w tym wierzchołek funkcji. Przydatne będą również punkty przecięcia z osią $OX$(o ile istnieją) i punkt przecięcia z osią $OY$ (wyraz wolny – c, lub inaczej wartość funkcji dla $x=0,$ czyli $f(0).$) Im więcej tych punktów wyznaczymy, np sporządzając tabelkę i podstawiając pod $x$ różne wartości, np.
|
$x$ |
$-3$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
$3$ |
|
$f(x)$ |
$f(-3)$ | $f(-2)$ | $f(-1)$ | $f(0)$ | $f(1)$ | $f(2)$ |
$f(3)$ |
i licząc wartości funkcji tym dokładniejszy będzie nasz wykres.
Krok1. Wyznaczamy wierzchołek paraboli.$W=(p, q)$
$\Delta=b^2-4ac=2^2-4\cdot(-1)\cdot3=4+12=16$
$p=\frac{-b}{2a}=\frac{-2}{-2}=1$
$q=\frac{-\Delta}{4a}=\frac{-16}{-4}=4$
$W=(p, q)$
Krok 2. Liczymy miejsca zerowe. Ponieważ $\Delta>0$ (co policzyliśmy w poprzednim kroku), to funkcja ma dwa miejsca zerowe.
$x_1=\frac{-b-\sqrt\Delta}{2a}=\frac{-2-\sqrt{16}}{-2}=\frac{-2-4}{-2}=\frac{-6}{-2}=3$
$x_2=\frac{-b+\sqrt\Delta}{2a}=\frac{-2+\sqrt{16}}{-2}=\frac{-2+4}{-2}=\frac{2}{-2}=-1$
Krok 3. Wyznaczamy punkt przecięcia z osią $OY$. Ten punkt ma współrzędne $(0, c)$, czyli w tym przypadku $(0, 3)$.
Krok 4. Mamy dużo informacji z poprzednich kroków, więc moglibyśmy pominąć ten krok, ale policzymy jeszcze wartości w pobliżu wierzchołka, żeby otrzymać ładniejszy wykres.
Skoro wierzchołek ma pierwszą współrzędną $p=1$, to policzmy wartości funkcji dla $x=0, x=2$ (oddalone o $1$ od wierzchołka) oraz dla $x=-1, x=3$ (oddalone o $2$ od wierzchołka) oraz dla $x=-2, x=4$ (oddalone o 3 od wierzchołka).
$f(0)=-0^2+2\cdot0+3=3$ Zatem do wykresu należy punkt $(0, 3)$ (ten punkt już tak naprawdę mieliśmy, to jest punkt przecięcia z osią $OY$).
$f(2)=-2^2+2\cdot2+3=3$ Zatem do wykresu należy punkt $(2, 3)$.
$f(-1)=-(-1)^2+2\cdot(-1)+3=0$ Zatem do wykresu należy punkt $(-1, 0)$ (ten punkt też już mieliśmy, to jest miejsce zerowe $x_2$).
$f(3)=-3^2+2\cdot3+3=0$ (Otrzymaliśmy drugie miejsce zerowe x_1$.)
$f(-2)=-(-2)^2+2\cdot(-2)+3=-5$ Otrzymaliśmy punkt $(-2, -5)$.
$f(4)=44^2+4\cdot4+3=-5$.
Krok 5. Teraz zaznaczamy wszystko na wykresie i rysujemy parabolę, czyli nasz wykres.
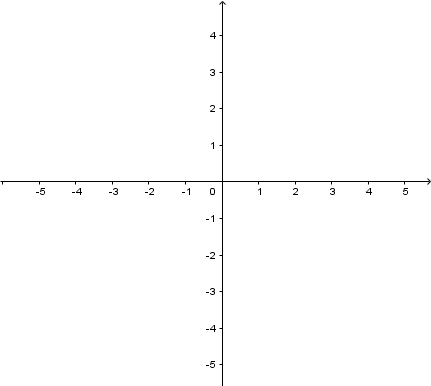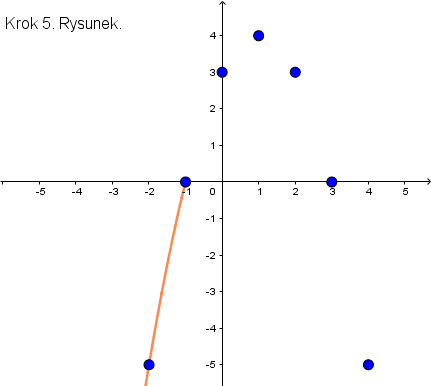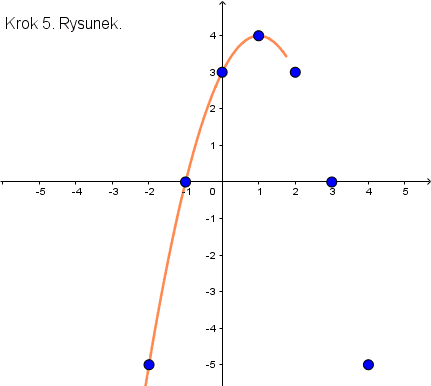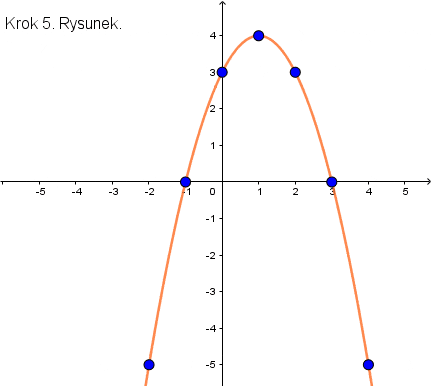
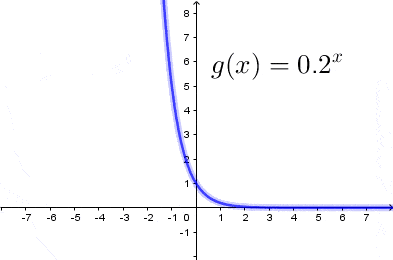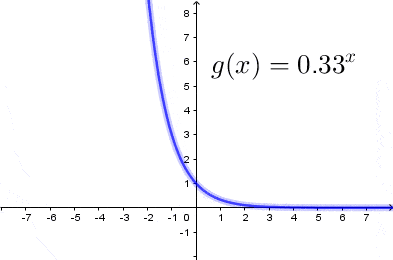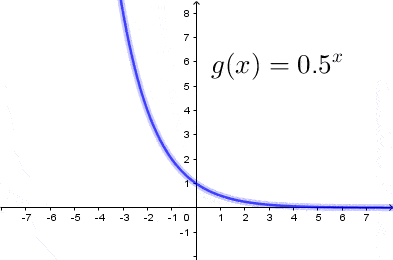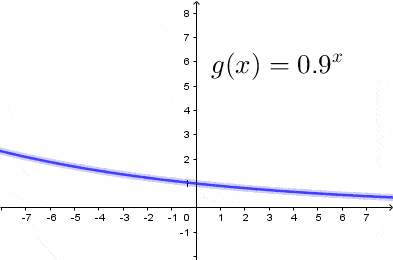
Jak narysować wykres funkcji wykładniczej
$$f(x)=a^x,$$
gdzie
- $a$ – stała
- $a>0$
Wykresem funkcji wykładniczej jest krzywa przechodząca przez punkt $(0,1)$ układu współrzędnych. Krzywa ta w całości znajduje się w pierwszej i drugiej ćwiartce układu współrzędnych i nigdy nie przecina odi $OX,$ oraz jest:
Aby narysować wykres funkcji wykładniczej, najłatwiej jest policzyć wartości funkcji dla kilku argumentów tworząc tabelkę podobną do tej:
|
$x$ |
$-3$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
$3$ |
|
$a^x$ |
$(\frac{1}{a})^3$ | $(\frac{1}{a})^2$ | $\frac{1}{a}$ | $1$ | $a$ | $a^2$ |
$a^3$ |
Sporządźmy tabelkę:
|
$x$ |
$-3$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
$3$ |
|
$f(x)$ |
$\frac{1}{27}$ | $\frac{1}{9}$ | $\frac{1}{3}$ | $1$ | $3$ | $9$ |
$27$ |
Zaznaczmy te punkty w układzie współrzędnych i przeprowadźmy przez nie linię.
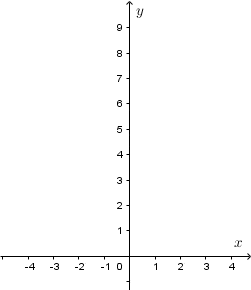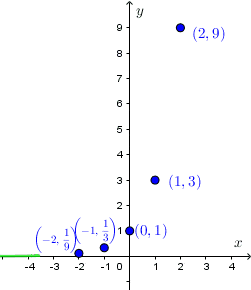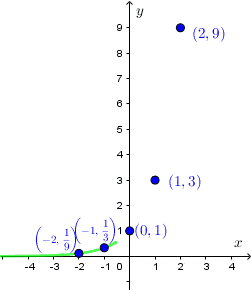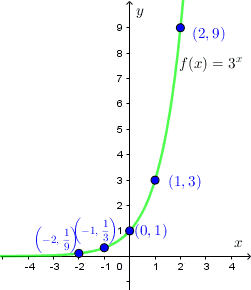
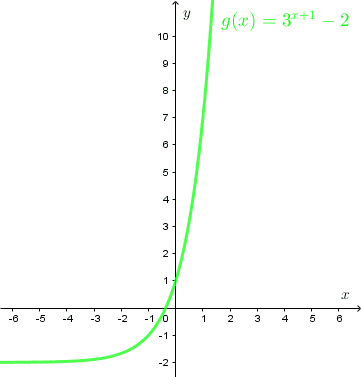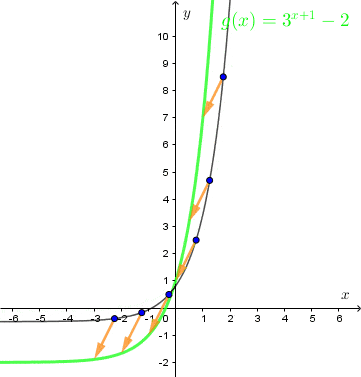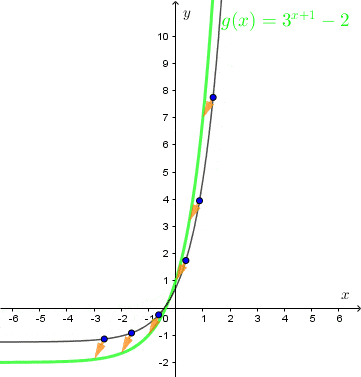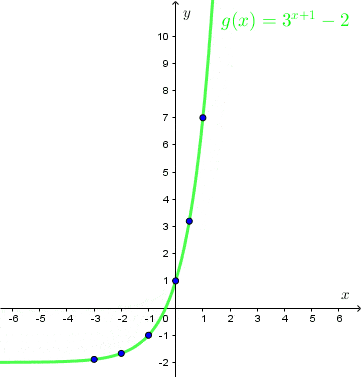

Matura z matematyki?
Oferujemy SuperKorepetycje - korki online połączone z przejrzyście zrozumiałymi filmikami do nauki własnej
Zobacz więcej