Zadania które tu omówimy to jest egzaminowy klasyk – jedno z najpopularniejszych typów zadań.
Ogólny schemat:
Mamy do policzenia prawdopodobieństwo np. $P(X\ge 160)$ gdzie $X$ jest zmienna losowa o rozkładzie normalnym $N(\mu\space \sigma)$ o danych parametrach $\mu$ i $\sigma$ (średnia i odchylenie standardowe)
Aby policzyć to prawdopodobieństwo, chcemy daną zmienną sprowadzić do rozkładu normalnego standaryzowanego o wartości oczekiwanej $\mu =0$ i odchyleniu standardowym $\sigma=1$

Po co?
Będziemy mogli skorzystać z tablic rozkładu $N(0,1)$, aby odczytać końcowe wartości prawdopodobieństw.
Schemat rozwiązywania zadań z rozkładem normalnym:
- Dane $\mu$ i $\sigma$
- Pytanie o prawdopodobieństwo $P(x_1 < X < x_2) =$?
- Standaryzacja (z dokładnością do 2 miejsc po przecinku) $\mu = \frac{x-\mu}{\sigma}$
- Pytanie o prawdopodobieństwo z użyciem zmiennej standaryzowanej $P(u_1 < U < u_2)=$?
- Rysunek pomocniczy.
- Tablice statystyczne.
- Odpowiedź.
Przykład
Wzrost kobiet w pewnej populacji ma rozkład normalny $N(165, 15)$. Oznacza to, że zmienna losowa jaką jest wzrost kobiet ma rozkład normalny ze średnią równą 165 cm odchyleniem standardowym równym 15 cm. Jaki jest udział w populacji kobiet o wzroście:
Wzrost kobiet w pewnej populacji ma rozkład normalny $N(165, 15)$. Oznacza to, że zmienna losowa jaką jest wzrost kobiet ma rozkład normalny ze średnią równą 165 cm odchyleniem standardowym równym 15 cm. Jaki jest udział w populacji kobiet o wzroście:
- do 160 cm
- w przedziale 165-170 cm
- powyżej 175 cm
- dokładnie 150 cm
Spróbuj rozwiązać to zadanie za pomocą widgetu.
Rozwiązanie
- Interesuje nas obliczenie prawdopodobieństwa zaznaczonego na niebiesko:
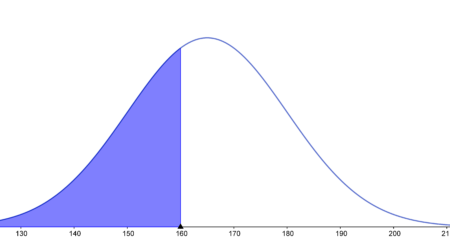
Robimy standaryzacje zmiennej losowej:
$$P(X < 106)=P \Big(\frac{x-\mu}{\sigma} < \frac{160-\mu}{\sigma} \Big)=$$
Możemy wprowadzić zmienną $U$ – zmienną losową rozkładu normalnego standaryzowanego i podstawiamy dane:
$$=P \Big(U < \frac{160-\mu}{\sigma} \Big)=P \Big(U < \frac{160-165}{15} \Big)=P(U < -0.333)=\Phi(-0.333)$$
Uwaga: W tablicach rozkładu normalnego najczęściej nie ma ujemnych wartości. Zatem stosujemy „przejście” w postaci: $\Phi(-\alpha)=1-\Phi(\alpha)$ bo dodatnią wartość już łatwo odnajdziemy w tablicach rozkładu normalnego.
$$\Phi(-0.333)=1-\Phi(0.333)=1-0.6293=0.3707$$
Odpowiedź: Szukane prawdopodobieństwo wynosi 37.07% (czyli pole zacieniowanej części wykresu wynosi 0.3707 na rysunku powyżej). - w przedziale 165-170 cm
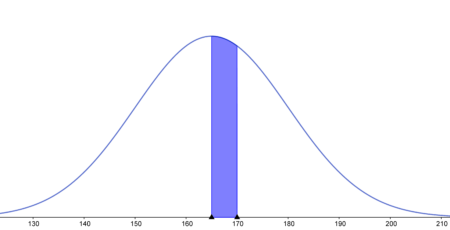
$P(165 < X < 170)=P \Big( \frac{165-165}{15} < \frac{X-165}{15} < \frac{170-165}{15} \Big)=P(0 < X < 0.33)=$ $\Phi(0.33)-\Phi(0)=0.6293-0.5=0.1293$
Odpowiedź: Szukane prawdopodobieństwo wynosi 12.93%. - powyżej 175 cm
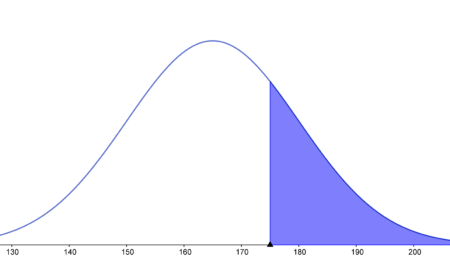
$P(X > 175)=P \Big( \frac{X-165}{15} > \frac{175-165}{15}\Big)=P(U > 0.67)= 1-P(U < 0.67)=1-$ $\Phi(0.67)=1-0.748571=0.251429$
Odpowiedź: Szukane prawdopodobieństwo wynosi 25.14%. - dokładnie 150 cm
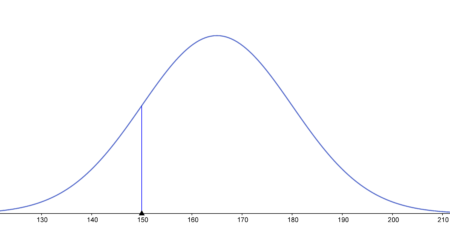
$P(X=15)=P(150 \le X \le 150)= F(150)-F(150)=0$ (bo dla zmiennych losowych ciągłych, prawdopodobieństwo w punkcie jest równe 0)
Odpowiedź: Prawdopodobieństwo wynosi 0.
Dla zmiennych losowych ciągłych (jak w przypadku rozkładu normalnego) zachodzi:
$$P(X < 165)=P(X \le 165)$$
$$P(X < 165)=P(X \le 165)$$
Przykład
Naszkicuj wykres gęstości zmiennej losowej X o rozkładzie normalnym $N(2, 0.5)$. Korzystając z tablic wartości dystrybuanty $\Phi$ rozkładu normalnego $N(0,1)$ oblicz:
Naszkicuj wykres gęstości zmiennej losowej X o rozkładzie normalnym $N(2, 0.5)$. Korzystając z tablic wartości dystrybuanty $\Phi$ rozkładu normalnego $N(0,1)$ oblicz:
- $P(X \le 1)$
- $P(X > 3)$
- $P(X > 0)$
Rozwiązanie
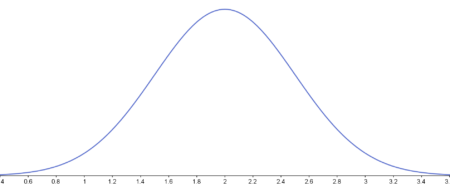

- $P(X \le 1)=P \Big(\frac{X-2}{0.5} \le \frac{1-2}{0.5} \Big)=\Phi(-2)=0.0227$
- $P(X > 3)=1-P(X \le 3)=1-\Phi \Big(\frac{3-2}{0.5} \Big)=1-\Phi(2)=\Phi(-2)=0.0227$
- $P(X > 0)=1-P(X \le 0)=1-\Phi \Big(\frac{0-2}{0.5} \Big)=1-\Phi(-4)=\Phi(4)=0.9999$
Przykład
Tutaj mamy podane prawdopodobieństwo (które wcześniej liczyliśmy), ale nie znamy wartości więc cały proces robimy „odwrotnie”.
Wysokość drzewa w pewnym lesie ma rozkład normalny ze średnią 25 m i odchyleniem standardowym 4 m. Planuję się wyciąć 26% najwyższych drzew. Od jakiej wysokości drzewa będą wycinane?
Tutaj mamy podane prawdopodobieństwo (które wcześniej liczyliśmy), ale nie znamy wartości więc cały proces robimy „odwrotnie”.
Wysokość drzewa w pewnym lesie ma rozkład normalny ze średnią 25 m i odchyleniem standardowym 4 m. Planuję się wyciąć 26% najwyższych drzew. Od jakiej wysokości drzewa będą wycinane?
Rozwiązanie
X- zmienna losowa o rozkładzie $N(25,4)$ oznaczająca wysokość drzewa
Szukamy takie $a$, że 26% drzew będzie większe od tej wartości
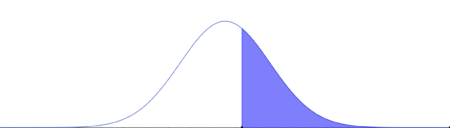
Pole zaznaczone na niebiesko odpowiada 26%
Czyli chcemy rozwiązać równanie:
$P(X > a)=0.26$, gdzie $a$ jest niewiadomą, a tym razem znamy wartość prawdopodobieństwa
$$1-P(X \ge a)=0.26$$ $$P(X \le a)=0.74$$Standaryzujmy zmienną X:
$$P\Big(\frac{X-25}{4} \le \frac{a-25}{4} \Big)=$$
Możemy użyć funkcji dystrybuanty rozkładu normalnego standaryzowanego:
$$=\Phi \Big(\frac{a-25}{4} \Big)=0.74$$
Teraz znajdujemy wartość odwrotną tej dystrybuanty- w tablicach szukamy takiego argumentu, dla którego funkcja daje 0.74
$$\frac{a-25}{4}=\Phi^{-1}(0.74)=0.643$$
Znaleźliśmy, że tą wartością jest 0.643
Przekształcamy równanie:
$$a=0.643 \cdot 4 +24=26.572$$
Odpowiedź: Zostaną wycięte drzewa większe od 26.572.
X- zmienna losowa o rozkładzie $N(25,4)$ oznaczająca wysokość drzewa
Szukamy takie $a$, że 26% drzew będzie większe od tej wartości

Pole zaznaczone na niebiesko odpowiada 26%
Czyli chcemy rozwiązać równanie:
$P(X > a)=0.26$, gdzie $a$ jest niewiadomą, a tym razem znamy wartość prawdopodobieństwa
$$1-P(X \ge a)=0.26$$ $$P(X \le a)=0.74$$Standaryzujmy zmienną X:
$$P\Big(\frac{X-25}{4} \le \frac{a-25}{4} \Big)=$$
Możemy użyć funkcji dystrybuanty rozkładu normalnego standaryzowanego:
$$=\Phi \Big(\frac{a-25}{4} \Big)=0.74$$
Teraz znajdujemy wartość odwrotną tej dystrybuanty- w tablicach szukamy takiego argumentu, dla którego funkcja daje 0.74
$$\frac{a-25}{4}=\Phi^{-1}(0.74)=0.643$$
Znaleźliśmy, że tą wartością jest 0.643
Przekształcamy równanie:
$$a=0.643 \cdot 4 +24=26.572$$
Odpowiedź: Zostaną wycięte drzewa większe od 26.572.
Bibliografia:
- Greń Jerzy, Statystyka matematyczna: Modele i zadania, Wyd. 4, Warszawa, PWN, 1974
- Rószkiewicz Małgorzata, Statystyka: Kurs podstawowy, Warszawa, EFEKT, 2002, ISBN 83-87338-15-X
25+
