Odległość punktu od prostej- teoria

Odległość punktu $P=(x_p,y_p)$ od prostej opisanej równaniem ogólnym prostej $Ax+By+C=0$ oznaczana $d$ jest to najmniejsza z odległości między nimi:$$\Large{d=\frac{\left|A\cdot x_p+B\cdot y_p+C\right|}{\sqrt{A^2+B^2}}}$$
Interpretacja geometryczna:
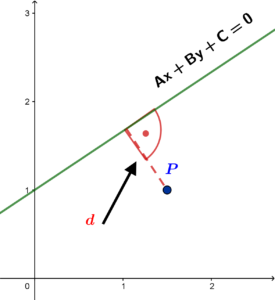
Uwaga: Tego nie musisz wkuwać! Wybrane wzory matematyczne – CKE strona 5.

Obliczanie odległości punktu od prostej

Przykład: Oblicz odległość punktu $P=(1,2)$ od prostej $k:$ $2x+4y-1=0$.

Łatwo zauważyć, że:

  • jeżeli $P=(1,2)$, to $x_p=1$ i $y_p=2$
  • jeżeli $2x+4y-1=0$, to $A=2$, $B=4$, $C=-1$
Mamy już wszystkie potrzebne dane 🙂 Podstawiamy do wzoru:

$$d=\frac{\left|A\cdot x_p+B\cdot y_p+C\right|}{\sqrt{A^2+B^2}}$$$$d=\frac{\left|2\cdot 1+4\cdot 2+(-1)\right|}{\sqrt{2^2+4^2}}$$

$$d=\frac{\left|2+8-1\right|}{\sqrt{20}}$$

$$d=\frac9{\sqrt{20}}$$

Odpowiedź: Odległość punktu $P$ od prostej $k$ wynosi $\frac9{\sqrt{20}}$.

Przykład: Oblicz odległość prostej $k:$ $-3+7y-5=0$ od początku układu współrzędnych.

Początek układu współrzędnych $P=(0,0)$, więc $x_p=0$ i $y_p=0$.
Jeżeli $-3+7y-5=0$, to $A=-3$, $B=7$, $C=-5$.

Podstawiamy do wzoru:

$$d=\frac{\left|A\cdot x_p+B\cdot y_p+C\right|}{\sqrt{A^2+B^2}}$$

$$d=\frac{\left|-3\cdot 0+7\cdot 0+(-5)\right|}{\sqrt{(-3)^2+(7)^2}}$$

$$d=\frac{\left|-5\right|}{\sqrt{58}}$$

Wiemy, że odległość jest dodatnia, więc:

$d=\frac5{\sqrt{58}}=$$\frac5{\sqrt{58}}\cdot 1$$=\frac5{\sqrt{58}}\cdot \frac{\sqrt{58}}{\sqrt{58}}$$=\frac{5\sqrt{58}}{58}$

Odpowiedź: Odległość punktu $P$ od prostej $k$ wynosi $\frac{5\sqrt{58}}{58}$.

Przykład: Oblicz odległość punktu $P=(1,0)$ od prostej $y=x-3$.

Aby obliczyć odległość punktu od prostej $y=x-3$ musimy przekształcić wzór funkcji w postaci kierunkowej do postaci ogólnej.
Przenosimy wszystko na jedną stronę:
$$y=x-3\hspace{0,5cm}|+3$$$$y+3=x\hspace{0,5cm}|-x$$$$-x+y+3=0$$
Mamy więc, że $x_p=1$ i $y_p=0$, $A=-1$, $B=1$, $C=3$.

Podstawiamy do wzoru:

$$d=\frac{\left|A\cdot x_p+B\cdot y_p+C\right|}{\sqrt{A^2+B^2}}$$

$$d=\frac{\left|-1\cdot 1+1\cdot 0+3\right|}{\sqrt{(-1)^2+1^2}}$$

$$d=\frac{\left|-1+3\right|}{\sqrt{2}}$$

$$d=\frac2{\sqrt{2}}=\sqrt2$$

Odpowiedź: Odległość punktu $P$ od prostej $y=x-3$ wynosi $\sqrt2$.

Obliczanie odległości dwóch prostych od siebie

Aby móc obliczyć odległość dwóch prostych od siebie sprawdzamy, czy są one prostymi równoległymi. Jeżeli tak, to do znanego wzoru podstawiamy $x_p$ oraz $y_p$ z prostej $k$ oraz $A$, $B$, $C$ z prostej $l$.

Kiedy dwie proste są równoległe?

Dwie proste o równaniach ogólnych:
$$A_1x+B_1y+C_1=0$$
$$A_2x+B_2y+C_2=0$$
są równoległe, gdy $$\Large{A_1B_2-A_2B_1=0}$$

Przykład: Oblicz odległości prostych $k:$ $2x+y-1=0$ i $l:$ $2x+y+4$ od siebie.

Sprawdźmy, czy proste są równoległe $\Leftrightarrow$ $A_1B_2-A_2B_1=0$.

Z treści zadania wiemy, że $A_1=2$, $A_2=2$, $B_1=1$, $B_2=1$.

$A_1B_2-A_2B_1=0$ $\Leftrightarrow$ $2\cdot 1-2\cdot 1=0$ $\Leftrightarrow$ $2-2=0$ $\Leftrightarrow$ $0=0$ $\Leftrightarrow$ $L=P$

Zatem proste $k$ i $l$ są równoległe, możemy obliczyć odległości między nimi.

Zauważmy, że do prostej $k$ należy punkt $P=(1,-1)$ $\Rightarrow$ $x_p=1$, $y_p=-1$.

Weźmy pod uwagę prostą $l:$ $2x+y+4$ $\Rightarrow$ $A=2$, $B=1$, $C=4$.

Podstawiamy do wzoru:

$d=\frac{\left|A\cdot x_p+B\cdot y_p+C\right|}{\sqrt{A^2+B^2}}$$=\frac{\left|2\cdot 1+1\cdot (-1)+4\right|}{\sqrt{2^2+1^2}}$$=\frac{\left|2-1+4\right|}{\sqrt{5}}=$$\frac5{\sqrt{5}}$$=\sqrt5$

Odpowiedź: Prosta $k$ jest oddalona od prostej $l$ o $\sqrt5$.

Przykład: Oblicz odległości prostych $k:$ $2x+y=0$ i $l:$ $-3x+y-1=0$ od siebie.

Sprawdźmy, czy proste są równoległe $\Leftrightarrow$ $A_1B_2-A_2B_1=0$.
Z treści zadania wiemy, że $A_1=2$, $A_2=-3$, $B_1=1$, $B_2=1$.
$A_1B_2-A_2B_1$$=2\cdot 1-(-3)\cdot 1$$=2+3$$=5$$\neq 0$
Proste $k$ i $l$ nie są równoległe, więc nie możemy obliczyć ich odległości od siebie.
Odpowiedź: Odległość między prostymi $k$ i $l$ nie jest jednoznaczna.
3+
Anita Księżak