Kula
Kula jest bryłą obrotową powstałą z obrotu o $360^{\circ}$ półkola o promieniu $r$ dookoła prostej zawierającej średnicę tego półkola, $r$ nazywamy promieniem kuli.
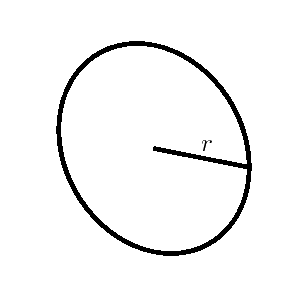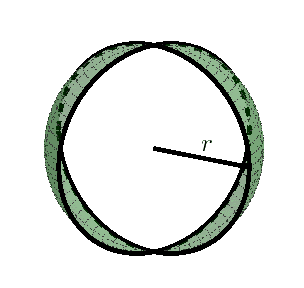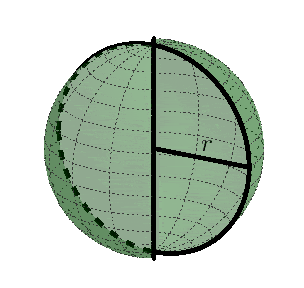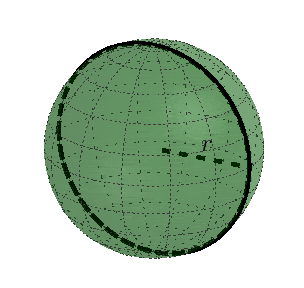
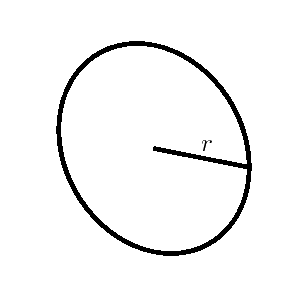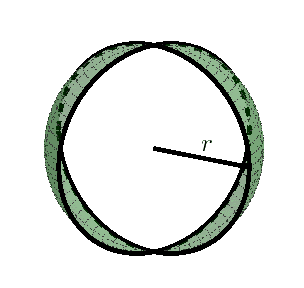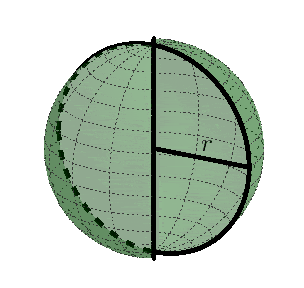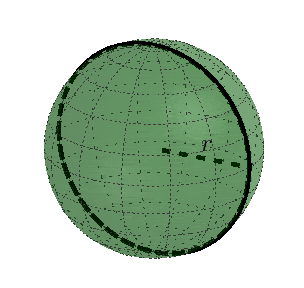
Kulę o promieniu $r$ można stworzyć w sposób równoważny, przez obrót o $180^{\circ}$ koła o promieniu $r$ dokoła prostej zawierającej średnicę tego koła.
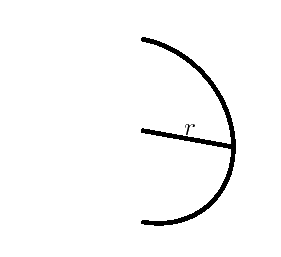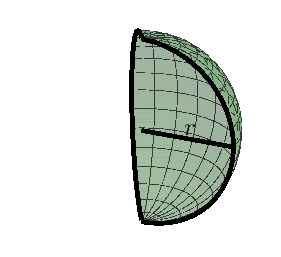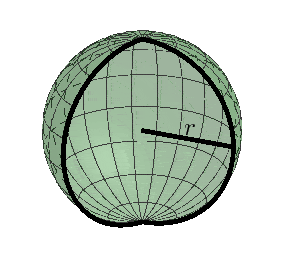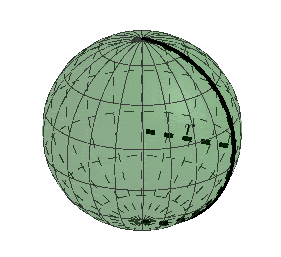
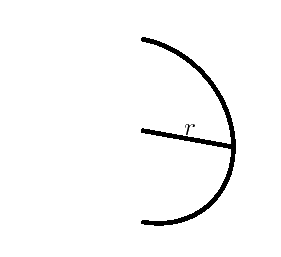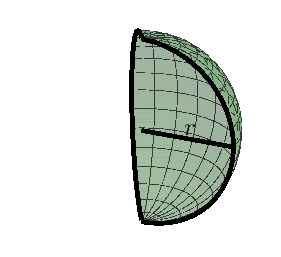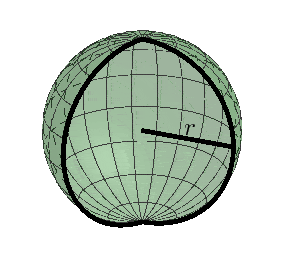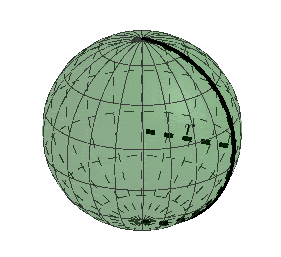
Objętość kuli
Objętość kuli wyraża się wzorem:
$$V=\frac{4}{3}\pi r^3$$
$$V=\frac{4}{3}\pi r^3$$
Pole powierzchni kuli
Pole powierzchni kuli wyraża się wzorem:
$$P=4\pi r^2$$
$$P=4\pi r^2$$
Przykład 1: Kula ma objętość $V=288\pi .$ Oblicz długość promienia tej kuli.
Wiemy, że
$V=228\pi $
Ze wzoru na objętość kuli mamy:
$228\pi =\frac{4}{3}\pi r^3 \quad \mid :\pi$
$228=\frac{4}{3}r^3 \quad \mid \cdot \frac{3}{4}$
$r^3=216$
$r=6$
Odpowiedź: Ta kula ma promień długości 6.
$V=228\pi $
Ze wzoru na objętość kuli mamy:
$228\pi =\frac{4}{3}\pi r^3 \quad \mid :\pi$
$228=\frac{4}{3}r^3 \quad \mid \cdot \frac{3}{4}$
$r^3=216$
$r=6$
Odpowiedź: Ta kula ma promień długości 6.
Przykład 2: Pole powierzchni kuli wynosi $64\pi .$ Oblicz objętość tej kuli.
Zacznijmy od wyliczenia $r$ ze wzoru na pole powierzchni kuli:
$64\pi =4\pi r^2 \quad :4\pi$
$r^2=16$
$r=4 \quad \vee \quad r=-4$
Ponieważ długość nie może być ujemna, więc $r=4.$
Teraz pozostaje podstawić otrzymane $r$ do wzoru na objętość kuli, aby otrzymać wynik.
$V=\frac{4}{3}\pi 4^3=\frac{256}{3}\pi$
Odpowiedź: Objętość tej kuli jest równa $\frac{256}{3}\pi.$
$64\pi =4\pi r^2 \quad :4\pi$
$r^2=16$
$r=4 \quad \vee \quad r=-4$
Ponieważ długość nie może być ujemna, więc $r=4.$
Teraz pozostaje podstawić otrzymane $r$ do wzoru na objętość kuli, aby otrzymać wynik.
$V=\frac{4}{3}\pi 4^3=\frac{256}{3}\pi$
Odpowiedź: Objętość tej kuli jest równa $\frac{256}{3}\pi.$
1+
