Ciąg arytmetyczny
Liczbę tę nazywamy różnicą. Jest ona stała i oznaczamy ją literą $r$.

W powyższym przykładzie różnica ${\color{#339966}r}=2$.
Na wykresie wszystkie wyrazy leżą na jednej linii:
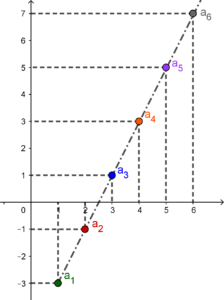
Ponieważ dwa wyrazy ciągu arytmetycznego różnią się o ${\color{#339966}r}$ to możemy je obliczyć ze wzoru
$$\Large{{\color{#339966}r}=a_{n+1} – a_n}$$
gdzie $a_{n+1}$ i $a_n$ są dwoma kolejnymi wyrazami ciągu arytmetycznego.
Podstawiamy do wzoru drugi i pierwszy wyraz ciągu:
$r=a_2 – a_1$
$r=a_2 – a_1= 8 – 2 = 6$
$ $
Analogicznie możemy też wziąć trzeci i drugi wyraz ciągu:
$a_2=8$, $a_3=14$
$r= 14-8 = 6$
$ $
Odpowiedź: Oba sposoby są poprawne, a różnica tego ciągu wynosi $6$.
Między np. pierwszym a piątym wyrazem są 4 różnice:
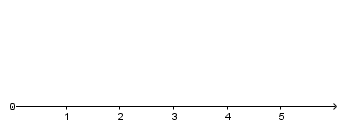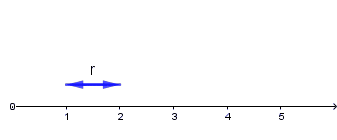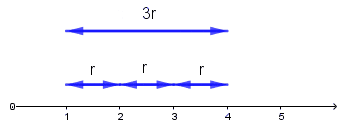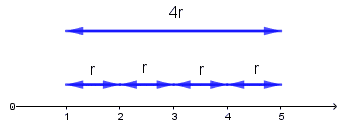
$n$-ty wyraz ciągu arytmetycznego
$$\Large{a_n = {\color{blue}a_1} + ({\color{red}n} – 1)\cdot {\color{#339966}r}}$$
gdzie:
$a_1$ – pierwszy wyraz ciągu arytmetycznego,
$r$ – różnica ciągu arytmetycznego,
$n$ – numer wyrazu, który chcemy obliczyć
Przykład: Wyznacz wzór ogólny dla ciągu o $a_1= 12$ i $r=8$.
$a_n = a_1 + (n – 1)\cdot r$
$a_n = 12 + (n – 1)\cdot 8$
$a_n = 12 + 8\cdot n – 8$
$a_n = 8\cdot n + 4$
$ $
Odpowiedź: Wzór ogólny tego ciągu to $a_n = 8\cdot n + 4$
Przykład: Wyznacz wzór na $n$-ty wyraz ciągu $-3, 0, 3, …$.
Zgodnie z informacjami z treści zadania pierwszy wyraz tego ciągu to $a_1 = – 3$.
Ponieważ mamy uzyskać wzór na $n$-ty wyraz to za $”n”$ nie podstawiamy żadnej liczby.
Brakuje nam tylko różnicy, czyli $r$. Obliczamy ją z poniższego wzoru:
$r=a_{n+1} – a_n$.
Zatem
$r=a_2 – a_1 = 0 -(- 2) = 3$.
Wstawiamy $r$ i $a_1$ do wzoru:
$a_n = a_1 + (n – 1)\cdot r$
$a_n = -3 + (n – 1)\cdot 3 $$ = -3 + 3\cdot n – 3 = 3\cdot n – 6$
Odpowiedź: Wzór na $n$-ty wyraz to $a_n = 3\cdot n – 6$.
$r=a_{n-1} – a_n$
Odejmujemy pierwszy wyraz ciągu od drugiego:
$r=a_2 – a_1= 8 – (- 3) = 11$
$ $
Mamy już $a_1$ i $r$, więc wstawiamy do wzoru ogólnego na $n$-ty wyraz:
$a_n = a_1 + (n – 1)\cdot r= (-3) + (n – 1)\cdot 11$$= (-3) + 11\cdot n – 11= 11\cdot n -14$
$ $
Odpowiedź: Różnica tego ciągu to $11$, a jego wzór na $n$-ty wyraz (wzór ogólny) to $a_n = 11\cdot n -14$.
Aby znaleźć różnicę potrzebujemy dwóch sąsiednich wyrazów. Najprościej będzie jak znajdziemy pierwszy i drugi wyraz ciągu (możemy wybrać dowolne dwa sąsiednie wyrazy, ale dobieramy takie, które są najprostsze w liczeniu). Odejmując je od siebie otrzymamy $r$ :
$a_1 = 10\cdot 1 + 120 = 10 + 120 = 130$
$a_2 = 10\cdot 2 + 120 = 20 + 120 = 140$
Odejmujemy pierwszy wyraz od drugiego:
$a_1-a_2=140-130=10$
Dziesiąty wyraz ciągu znajdziemy z podanego w treści zadania wzoru – wystarczy wstawić za $n$ liczbę $10$ :
$a_{10} = 10\cdot 10 + 120 = 100 + 120 $$= 220$.
Odpowiedź: Różnica tego ciągu wynosi $10$, a dziesiąty wyraz $220$.
Wystarczy więc odjąć $a_{11} – a_1$ i podzielić na $10$, aby otrzymać różnicę:$r = \frac{a_{11}-a_1}{10} = \frac{40 – 10}{10} = \frac{30}{10} = 3$
Zatem różnica $r = 3$.
$ $
Ponieważ mamy już $a_1$ i $r$ to możemy wstawić je do wzoru (tak jak w poprzednim przykładzie):
$a_n = a_1 + (n – 1)\cdot r $$= 10 + 3\cdot (n-1) $$= 10 + 3\cdot n – 3 $$= 3\cdot n + 7$
$ $
Odpowiedź: Wzór na n-ty wyraz tego ciągu to $a_n = 3\cdot n + 7$, a różnica $r = 3$.
$r = \frac{a_{12}-a_{10}}{2} = \frac{39 – 29}{2} = \frac{10}{2} = 5$
Aby znaleźć $a_1$ używamy wzoru na $n$-ty wyraz, czyli $a_n = a_1 + (n – 1)\cdot r$, gdzie za $a_n$ podstawiamy $a_{10}$ – wtedy $n = 10$, bo $a_{10}$ to dziesiąty wyraz tego ciągu.
Obliczyliśmy już różnicę tego ciągu, więc jedyną niewiadomą w równaniu pozostaje $a_1$:
$ 29 = a_1 + (10 – 1)\cdot 5$
Przekształcamy równanie tak, aby po lewej stronie znalazło się $a_1$, a po prawej liczba:
$29=a_1 + 45$
$a_1 = -16$
Mając $a_1$ i $r$, jak w poprzednich zadaniach, wstawiamy je do wzoru:
$a_n = a_1 + (n – 1)\cdot r $$= (-16) + 5\cdot (n-1)$$ = (-16) + 5\cdot n – 5 = 5\cdot n + 21$
Odpowiedź: Otrzymujemy, że $a_{1}=-16$ oraz $r = 5$, zaś wzór ogólny ciągu to $a_n = 5\cdot n + 21$.
