Trójkąty przystające


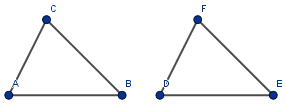
Trójkąty są przystające, jeżeli mają takie same długości boków i takie same miary kątów – mają identyczny kształt i rozmiar.

Jak rozpoznać, czy dwa trójkąty są przystające?

$(1)$ cecha $\color{blue}{bbb}$ bok-bok-bok

trzy boki jednego trójkąta są równe trzem bokom drugiego trójkąta

  • $|AB|=|DE|$, $|AC|=|DF|$, $|BC|=|EF|$


$(2)$ cecha $\color{blue}{bkb}$ bok-kąt-bok

dwa boki i kąt zawarty między nimi zawarty w jednym trójkącie są odpowiednio równe dwóm bokom i kątowi między nimi w drugim trójkącie

  • $|AB|=|DE|$, $|AC|=|DF|$, $∡ BAC=∡ EDF$


$(3)$ cecha $\color{blue}{kbk}$ kąt-bok-kąt

bok i dwa leżące przy nim kąty w jednym trójkącie są równe bokowi i dwóm leżącym przy nim kątom
w drugim trójkącie

  • $|AB|=|DE|$, $|∡BAC|=|∡EDF|$, $|∡ABC|=|∡DEF|$

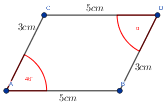
Przykład: Ile wynosi miara kąta $\alpha$ poniższej figury?

Trójkąty $△ABC$ i $△BCD$ mają trzy boki równej długości. Mają wspólny bok $BC$, $|AB|=|CD|$ oraz $|AC|=|BD|$. Zatem są one przystające.

Zauważmy, że miarę kąta $\alpha$ możemy odczytać korzystając z cechy $bkb$. Mamy, że $|AC|=|BD|$ oraz $|AB|=|BD|$ zatem $|∡BAC|=|∡BDC|$. Wynika z tego, że $\alpha=112°$.

Odpowiedź: Szukany kąt ma miarę $112°$.

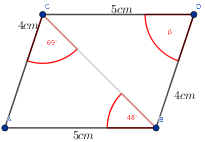
Przykład: Ile wynosi miara kąta $\beta$ poniższej figury?

Trójkąty $△ABC$ i $△BCD$ mają wspólny bok $BC$, oraz $|AB|=|CD|$ i $|AC|=|BD|$.
Są one przystające. Zauważmy, że z cechy $bkb$ mamy, że $|∡BAC|=|∡BDC|$.
Obliczmy miarę kąta $|∡BAC|$ korzystając z rysunku.

Wiemy, że suma miar kątów w trójkącie wynosi $180°$, zatem

$$|∡BAC|+|∡ABC|+|∡BCA|=180°$$

$$|∡BAC|+48°+69°=180°$$

$$|∡BAC|=63° \Rightarrow |∡BDC|=\beta=63°$$

Odpowiedź: Miara kąta $\beta$ wynosi $63°$.

Trójkąty podobne


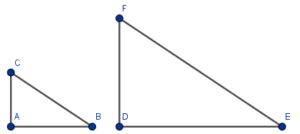
Trójkąty są podobne, jeżeli jeden jest “zmniejszeniem” lub “zwiększeniem” drugiego w pewnej skali.

Jak rozpoznać, czy dwa trójkąty są podobne?

$(1)$ cecha $\color{blue}{bbb}$ bok-bok-bok

trzy boki jednego trójkąta są proporcjonalne do trzech boków drugiego trójkąta

  • $\frac{AB}{CD}=\frac{AC}{DF}=\frac{BC}{EF}$


$(2)$ cecha $\color{blue}{bkb}$ bok-kąt-bok

dwa boki jednego trójkąta są proporcjonalne do dwóch boków drugiego trójkąta oraz kąty zawarte między tymi bokami są równe

  • np. $\frac{AB}{DE}=\frac{AC}{DF}$, $|∡BAC|=|∡EDF|$


$(3)$ cecha $\color{blue}{kkk}$ kąt-kąt-kąt

kąty jednego trójkąta są równe kątom drugiego trójkąta

  • $|∡BAC|=|∡EDF|$, $|∡ABC|=|∡DEF|$, $|∡ACD|=|∡DFE|$
Uwaga: Gdy skala jest równa 1, trójkąty podobne są jednocześnie przystające.
Przykład: Sprawdź, czy poniższe trójkąty są podobne.
Skorzystamy z cechy podobieństwa bok-bok-bok. Porównajmy do siebie dwa kolejne boki: najdłuższe, najkrótsze, pozostałe.

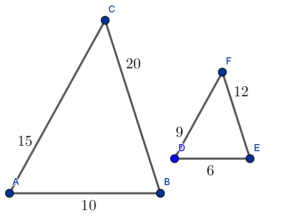
Najdłuższe: $\frac{12}{20}=\frac35$

Najkrótsze: $\frac6{10}=\frac35$

Pozostałe: $\frac9{15}=\frac35$

Odpowiedź: Z proporcjonalności boków trójkąty są podobne na mocy cechy $bbb$.

Przykład 2.2 Wyznacz długość odcinka $CE$ wiedząc, że $BD||CE$.

Proste $BD$ i $CE$ są do siebie równoległe, dlatego $|∡ABD|=|∡ACE|$, $|∡ADB|=|∡AEC|$ oraz $|∡BAD|=|∡CAE|$. Możemy zauważyć, że $△ABD \approx △ACE$
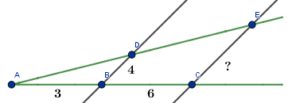
(czyli $△ABD$ jest podobny do $△ACE$) na mocy cechy $kkk$.

Z podobieństwa mamy, że:

$$\frac{AB}{AC}=\frac{BD}{CE}$$

$$\frac39=\frac4{CE}$$

Z metody “na krzyż”:

$$3|CE|=4\cdot 9$$

$$3|CE|=36|:3$$

$$|CE|=12$$

Odpowiedź: Długość odcinka $CE$ wynosi 12.

Przykład: Dwa zewnętrznie styczne okręgi są styczne do ramion pewnego kąta. Odległości ich środków od wierzchołka kąta wynoszą 15 i 20. Oblicz długości promieni tych okręgów $R$ i $r$.

$R+r=20-15=5$

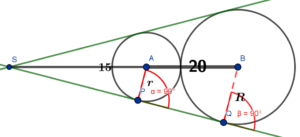
Trójkąty $△APS$ i $△BQS$ są podobne na mocy cechy kąt-kąt-kąt, stąd:
$\frac Rr=$$\frac{R+r+15}15$$\Leftrightarrow \frac Rr=\frac{20}{15}$$\Leftrightarrow \frac Rr=\frac43$$\Leftrightarrow R=\frac43r$

Wiemy, że $R+r=5$.
$R+r=5$$\Leftrightarrow$ $($wstawiamy $R=\frac43$$)$ $\Leftrightarrow\frac43r+r=5$$\Leftrightarrow \frac73r=5$$r=\frac{15}7$
Stąd $R=\frac43r=$$\frac43\cdot \frac{15}7=$$\frac{20}7$.
Odpowiedź: Mamy, że $R=\frac{20}7$ i $r=\frac{15}7$.

Podobieństwo a pole

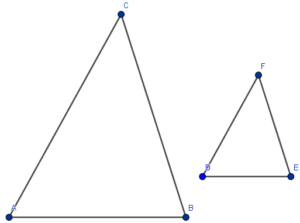Jeżeli $△ABC \approx △DEF$ na mocy cechy bok-bok-bok , to $\frac{AB}{CD}$$=\frac{AC}{DF}$$=\frac{BC}{EF}$$=m$, gdzie $\color{red}{m}$ jest skalą podobieństwa trójkąta $△ABC$ do $△DEF$ to:

$\frac{P_{△ABC}}{P_{△DEF}}= \color{red}{m^2}$

Stosunek pola trójkąta $△ABC$ do pola trójkąta $△DEF$ jest równy $\color{red}{skali\>podobieństwa\>m}$ podniesionej do kwadratu.

Uwaga: Ten wzór musisz zapamiętać! Nie znajdziesz go w karcie wzorów.

Przykład: Niech $△ABC$ będzie podobny do trójkąta $△DEF$ oraz $P_{△ABC}=28cm^2<P_{△DEF}$. Oblicz pole trójkąta $△DEF$ wiedząc, że stosunek długości boków mniejszego trójkąta do długości boków większego trójkąta wynosi $2/3$.

Z treści zadania wiemy, że skala podobieństwa $△ABC$ do $△DEF$ wynosi $m=\frac23$.
Korzystając z tego, że $P_{△ABC}=28[j]^2$ obliczymy $P_{△DEF}$.
Z twierdzenia dotyczącego związku podobieństwa trójkątów do pola mamy, że

$\frac{P_{△ABC}}{P_{△DEF}}=$$m^2=(\frac23)^2=$$\frac49$

$\frac{28cm^2}{P_{△DEF}}=\frac49$

Z metody “na krzyż” mamy, że

$9\cdot 28 cm^2=4\cdot P_{△DEF}$

$252cm^2=4\cdot P_{△DEF}|:4$

$P_{△DEF}=63cm^2$

Odpowiedź: Z podobieństwa trójkątów wiemy, że $P_{△DEF}=63cm^2$.
9+
Anita Księżak