Wyznaczanie prostej przechodzącej przez dwa punkty

Pokażemy jak wyznaczyć prostą przechodzącą przez dwa punkty.
Wyobraź sobie układ współrzędnych, umieść na nim dwa dowolne punkty (gdziekolwiek 🙂 ). Spróbuj je ze sobą połączyć, a teraz po prostu przedłuż ten odcinek. Gotowe!

Rozwiązując zadania przyjmujemy z góry, że $A=(x_a,y_a)$ i $B=(x_b,y_b)$. Nie ma znaczenia który z punktów będzie brany pod uwagę jako pierwszy.
Gdy znamy już punkty $A$ i $B$, to możemy wyznaczyć równanie prostej przechodzącej przez dwa punkty.

Istnieją na to dwa sposoby – wybierz ten prostszy dla siebie.

Sposób 1

Równanie prostej, która przechodzi przez dwa dane punkty $A=(x_a,y_a)$, $B=(x_b,y_b)$:

$$\Large{(y-y_a)(x_b-x_a)-(y_b-y_a)(x-x_a)=0}$$
Uwaga: Tego nie musisz wkuwać! Wybrane wzory matematyczne – CKE strona 5.
Przykład: Wykres funkcji $f$ przechodzi przez dwa punkty $A=(2,5)$ i $B=(4,7)$. Znajdź wzór funkcji $f$.

Znamy ogólny wzór na równanie prostej przechodzącej przez dwa punkty $A$ i $B$.

Wiemy, że $A=(2,5)$ i $B=(4,7)$, a nasze rozwiązanie będzie miało postać ${\color[rgb]{0.0, 0.5, 0.0}y}=a{\color[rgb]{1.0, 0.22, 0.0}x}+b$, gdzie $a$ i $b$ są dowolnymi liczbami rzeczywistymi.

Czego potrzebujemy do uzupełnienia wzoru

$({\color[rgb]{0.0, 0.5, 0.0}y}-y_a)(x_b-x_a)-(y_b-y_a)({\color[rgb]{1.0, 0.22, 0.0}x}-x_a)=0$

?

${\color[rgb]{1.0, 0.22, 0.0}x}$ oraz ${\color[rgb]{0.0, 0.5, 0.0}y}$ są zmiennymi, co oznacza że na stałe znajdują się w naszym zbiorze – nie podstawiamy za nie żadnej liczby. Musimy więc znaleźć $x_a$, $y_a$, $x_b$, $y_b.$

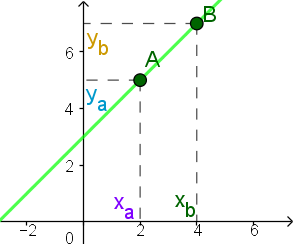
Wiemy, że w ogólności $A=({\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}x}_a},{\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}y}_a})$ i $B=({\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}x}_b},{\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}y}_b})$.

Mamy, że $A=({\color[rgb]{0.0, 0.0, 0.5}2},{\color[rgb]{0.0, 0.5, 0.5}5})$ i $B=({\color[rgb]{0.0, 0.5, 0.0}4},{\color[rgb]{0.51, 0.5, 0.0}7})$, więc ${\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}x}_a}{\color[rgb]{0.0, 0.0, 0.5}=}{\color[rgb]{0.0, 0.0, 0.5}2}$, ${\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}y}_a}{\color[rgb]{0.0, 0.5, 0.5}=}{\color[rgb]{0.0, 0.5, 0.5}5}$, ${\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}x}_b}{\color[rgb]{0.0, 0.5, 0.0}=}{\color[rgb]{0.0, 0.5, 0.0}4}$, ${\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}y}_b}{\color[rgb]{0.51, 0.5, 0.0}=}{\color[rgb]{0.51, 0.5, 0.0}7}$.

Podstawiamy do następującego wzoru i gotowe 🙂

$({\color[rgb]{0.0, 0.5, 0.0}y}-y_a)(x_b-x_a)-(y_b-y_a)({\color[rgb]{1.0, 0.22, 0.0}x}-x_a)=0$
$({\color[rgb]{0.0, 0.5, 0.0}y}-5)(4-2)-(7-5)({\color[rgb]{1.0, 0.22, 0.0}x}-2)=0$ Wykonujemy działania w nawiasach
$(y-5)2-2(x-2)=0$
$2y-10-2x+4=0$
$2y-2x-6=0$ Po lewej stronie zostaje sam $y$
$y=2x+6$ |: $2$
$y=x+3$ – postać kierunkowa

Odpowiedź: Równianie prostej przechodzącej przez dwa dane punkty ma postać $y=x+3$.

Jak sprawdzić poprawność swojej odpowiedzi?
Skoro przez oba punkty przechodzi jedna prosta to $A=(2,5)$ i $B=(4,7)$ spełniają równanie $y=x+3$. Co to oznacza?

$y_a=x_a+3$ i jednocześnie $y_b=x_b+3$

Jeżeli po podstawieniu $A=(2,5)$ i $B=(4,7)$ obie strony równań będą identyczne (L=P), to masz pewność że poprawnie wyznaczyłeś zadane równanie.

$y_a=x_a+3$ $y_b=x_b+3$
 
Podstawiamy
 
$5=2+3$ $7=4+3$
$5=5$ $7=7$
L=P L=P

L=P w obu przypadkach, więc nasze rozwiązanie jest prawidłowe 🙂

Przykład: Wykres funkcji $f$ przechodzi przez punkt $A=(2,6)$ i $f(-1)=3$. Znajdź wzór funkcji $f$.
Wiemy, że $f({\color[rgb]{0.0, 0.5, 0.0}-}{\color[rgb]{0.0, 0.5, 0.0}1})={\color[rgb]{0.51, 0.5, 0.0}3}$, czyli $B=({\color[rgb]{0.0, 0.5, 0.0}-1},{\color[rgb]{0.51, 0.5, 0.0}3})$. Mamy już wszystkie potrzebne informacje:
$A=({\color[rgb]{0.0, 0.0, 0.5}2},{\color[rgb]{0.0, 0.5, 0.5}6})$ i $B=({\color[rgb]{0.0, 0.5, 0.0}-1},{\color[rgb]{0.51, 0.5, 0.0}3})$, więc ${\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}x}_a}{\color[rgb]{0.0, 0.0, 0.5}=}{\color[rgb]{0.0, 0.0, 0.5}2}$, ${\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}y}_a}{\color[rgb]{0.0, 0.5, 0.5}=}{\color[rgb]{0.0, 0.5, 0.5}6}$, ${\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}x}_b}{\color[rgb]{0.0, 0.5, 0.0}=}{\color[rgb]{0.0, 0.5, 0.0}-1}$, ${\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}y}_b}{\color[rgb]{0.51, 0.5, 0.0}=}{\color[rgb]{0.51, 0.5, 0.0}3}$.
$ $

$({\color[rgb]{0.0, 0.5, 0.0}y}-y_a)(x_b-x_a)-(y_b-y_a)({\color[rgb]{1.0, 0.22, 0.0}x}-x_a)=0$
$({\color[rgb]{0.0, 0.5, 0.0}y}-6)(-1-2)-(3-6)({\color[rgb]{1.0, 0.22, 0.0}x}-2)=0$ Wykonujemy działania w nawiasach
$(y-6)(-3)-(-3)(x-2)=0$  | $-(-3)$= $+3$
$(y-6)(-3)+3(x-2)=0$
$-3y+18+3x-6=0$
$-3y+3x+12=0$ Po lewej stronie zostaje sam $y$
$-3y=3x+12$ |: $3$
$y=x+4$ – postać kierunkowa

Odpowiedź: Równanie prostej przechodzącej przez dwa dane punkty ma postać $y=x+4$.

Sposób 2

Równanie prostej przechodzącej przez dwa punkty $A=({\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}x}_a},{\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}y}_a})$ i $B=({\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}x}_b},{\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}y}_b})$ można wyznaczyć za pomocą danego układu równań:
$$\Large{\left\{\begin{array}{l}{\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}y}_a}=a{\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}x}_a}+b\\{\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}y}_b}=a{\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}x}_b}+b\end{array}\right.}$$
Przykład: Wykres funkcji $f$ przechodzi przez dwa punkty $A=(2,5)$ i $B=(4,7)$. Znajdź wzór funkcji $f$.
Znamy ogólny wzór funkcji liniowej ${\color[rgb]{0.0, 0.5, 0.0}y}=a{\color[rgb]{1.0, 0.22, 0.0}x}+b$, gdzie $a$ i $b$ są dowolnymi liczbami rzeczywistymi.
Z treści zadania wiemy, że $A=({\color[rgb]{0.0, 0.0, 0.5}2},{\color[rgb]{0.0, 0.5, 0.5}5})$ i $B=({\color[rgb]{0.0, 0.5, 0.0}4},{\color[rgb]{0.51, 0.5, 0.0}7})$, więc ${\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}x}_a}{\color[rgb]{0.0, 0.0, 0.5}=}{\color[rgb]{0.0, 0.0, 0.5}2}$, ${\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}y}_a}{\color[rgb]{0.0, 0.5, 0.5}=}{\color[rgb]{0.0, 0.5, 0.5}5}$, ${\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}x}_b}{\color[rgb]{0.0, 0.5, 0.0}=}{\color[rgb]{0.0, 0.5, 0.0}4}$, ${\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}y}_b}{\color[rgb]{0.51, 0.5, 0.0}=}{\color[rgb]{0.51, 0.5, 0.0}7}$.

Podstawiamy odpowiednio do wzoru:
$\left\{\begin{array}{l}{\color[rgb]{0.0, 0.5, 0.5}{\color[rgb]{0.0, 0.5, 0.5}y}_a}=a{\color[rgb]{0.0, 0.0, 0.5}{\color[rgb]{0.0, 0.0, 0.5}x}_a}+b\\{\color[rgb]{0.51, 0.5, 0.0}{\color[rgb]{0.51, 0.5, 0.0}y}_b}=a{\color[rgb]{0.0, 0.5, 0.0}{\color[rgb]{0.0, 0.5, 0.0}x}_b}+b\end{array}\right.$
$\left\{\begin{array}{l}{\color[rgb]{0.0, 0.5, 0.5}5}={\color[rgb]{0.0, 0.0, 0.5}2}{\color[rgb]{0.1, 0.1, 0.1}a}+b\\{\color[rgb]{0.51, 0.5, 0.0}7}={\color[rgb]{0.0, 0.5, 0.0}4}{\color[rgb]{0.1, 0.1, 0.1}a}+b\end{array}\right.$
Od drugiego równania odejmujemy pierwsze:
$7-5=4\cdot{\color[rgb]{1.0, 0.0, 0.0}a}-2\cdot{\color[rgb]{1.0, 0.0, 0.0}a}+{\color[rgb]{0.5, 0.0, 0.0}b}-{\color[rgb]{0.5, 0.0, 0.0}b}$
$2=2\cdot{\color[rgb]{1.0, 0.0, 0.0}a}$
Zamieniamy miejscami i dzielimy przez 2
${\color[rgb]{1.0, 0.0, 0.0}a}=1$

Podstawiamy ${\color[rgb]{1.0, 0.0, 0.0}a}=1$ do dowolnego z równań aby wyznaczyć ${\color[rgb]{0.5, 0.0, 0.0}b}$.
Oba sposoby znalezienia  ${\color[rgb]{0.5, 0.0, 0.0}b}$ są poprawne, wybierz łatwiejszy 🙂

$5={\color[rgb]{1.0, 0.0, 0.0}a}\cdot2+{\color[rgb]{0.5, 0.0, 0.0}b}$ $7={\color[rgb]{1.0, 0.0, 0.0}a}\cdot4+{\color[rgb]{0.5, 0.0, 0.0}b}$
$5=2+{\color[rgb]{0.5, 0.0, 0.0}b}$ $7=4+{\color[rgb]{0.5, 0.0, 0.0}b}$
${\color[rgb]{0.5, 0.0, 0.0}b}=3$ ${\color[rgb]{0.5, 0.0, 0.0}b}=3$

Mamy więc, że ${\color[rgb]{1.0, 0.0, 0.0}a}=1$ oraz ${\color[rgb]{0.5, 0.0, 0.0}b}=3$. Podstawiamy do ogólnego wzoru

$y={\color[rgb]{1.0, 0.0, 0.0}a}\cdot x+{\color[rgb]{0.5, 0.0, 0.0}b}$
$y={\color[rgb]{1.0, 0.0, 0.0}1}\cdot x+{\color[rgb]{0.5, 0.0, 0.0}3}$
$y=x+{\color[rgb]{0.5, 0.0, 0.0}3}$

Odpowiedź: Równianie prostej przechodzącej przez dwa dane punkty ma postać $y=x+3$.

1+
Anita Księżak