Argumenty i wartości funkcji
Aby dobrze zrozumieć czym są argumenty i wartości funkcji, wpierw należy przypomnieć czym dokładnie jest funkcja.
Niech dane będą dwa zbiory $X$ oraz $Y$. Funkcją nazywamy takie przyporządkowanie, które każdemu elementowi ze zbioru $X$ przyporządkowuje dokładnie jeden element ze zbioru $Y.$
Przykłady:
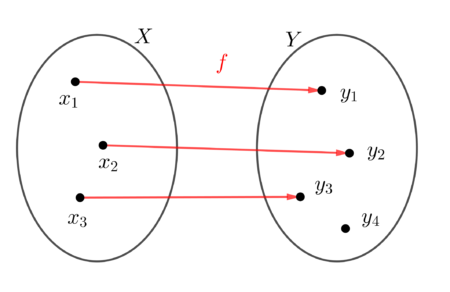
To przyporządkowanie jest funkcją.
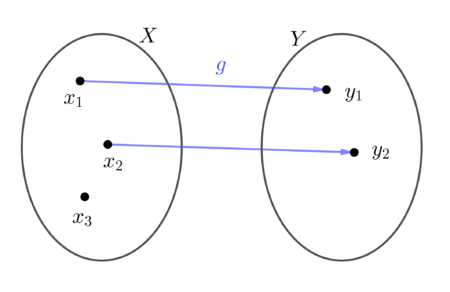
To przyporządkowanie nie jest funkcją, gdyż do elementu $x_{3}\in X$ nie przyporządkowano żadnego $y\in Y$.
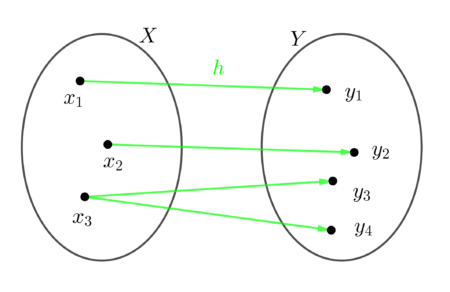
To przyporządkowanie nie jest funkcją, gdyż elementowi $x_{3}\in X$ przyporządkowano dwa elementy zbioru $Y$($y_{3}$ i $y_{4}$).
Ten przypadek wzbogacimy dodatkowo o odwzorowanie na wykresie. Zauważmy, że np. okrąg nie jest funkcją, gdyż dla pewnego $x\in X$ istnieją dwa różne $y\in Y.$
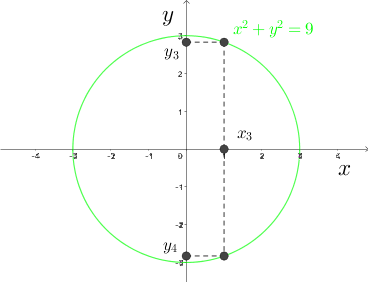

Teraz możemy przejść do zdefiniowania pojęć argumentu i wartości funkcji.
Argumentami funkcji nazywamy elementy zbioru $X,$ czyli zbioru z którego działa funkcja.
Wartościami funkcji nazywamy nazywamy te elementy zbioru $Y$(czyli zbioru w który działa funkcja), które zostały przyporządkowane do elementów zbioru $X$.
Podsumowując, gdy $x\in X$ oraz $y\in Y$
$$\overbrace{f(\underbrace{x}_{Argument})}^{Wartość funkcji}=\overbrace{y}^{Wartość funkcji}$$
Wartości funkcji możemy odczytać rzutując wykres funkcji na oś OY. Argumenty – na oś OX.
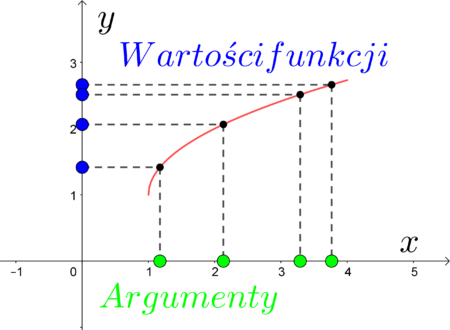
Zbiór wszystkich argumentów funkcji nazywamy dziedziną, zaś zbiór wszystkich wartości funkcji nazywamy zbiorem wartości.
Przykład 1: Dla jakiego argumentu funkcja $f(x)=-2x+3$ przyjmuje wartość 10?
W zadaniu pada pytanie o argument, czyli naszą szukaną jest takie $x,$ aby $f(x)=10$
$10=f(x)=-2x+3$
$10=-2x+3\quad \mid -3$
$7=-2x\quad \mid \cdot (-\frac{1}{2})$
$-3,5=x$
Odpowiedź: Funkcja przyjmuje wartość 10 dla argumentu $x=-3,5.$
$10=f(x)=-2x+3$
$10=-2x+3\quad \mid -3$
$7=-2x\quad \mid \cdot (-\frac{1}{2})$
$-3,5=x$
Odpowiedź: Funkcja przyjmuje wartość 10 dla argumentu $x=-3,5.$
Przykład 2: Jaką wartość przyjmuje funkcja $f(x)=-2x+3$ dla argumentu $x=3.$
W zadaniu pada pytanie o wartość funkcji, zatem naszą szukaną jest $f(x),$ gdy $x=3.$
$f(3)=-2\cdot 3+3=-3$
Odpowiedź: Dla argumentu $x=3$ funkcja przyjmuje wartość $f(x)=-3.$
$f(3)=-2\cdot 3+3=-3$
Odpowiedź: Dla argumentu $x=3$ funkcja przyjmuje wartość $f(x)=-3.$
23+
