Współczynnik korelacji rang Spearmana (RHO Spearmana) wykorzystywany jest do opisu siły korelacji dwóch cech, w przypadku gdy:

  • cechy mają charakter jakościowy, pozwalający na uporządkowanie ze względu na siłę tej cechy,
  • cechy mają charakter ilościowy, ale ich liczebność jest niewielka.

Wzór na współczynnik korelacji rang Spearmana

$$\huge{r_{s} = 1 – \frac{6 \sum_{i=1}^{n} d_{i}^{2}}{n \ \left(n^{2} – 1\right)}}$$,
gdzie:
$d_{i}^{2}$ – kwadraty różnic pomiędzy rangami odpowiadających sobie wartości cech $x_{i}$ i $y_{i}$.
$n$ – liczba par danych (liczba wierszy w tabeli).

Czym są rangi Spearmana?

Nadajemy cechom X i Y rangi (1- dla największej wartości X, 2 dla drugiej największej wartości X itd. I analogicznie dla Y).

Inaczej mówiąc, przyporządkujemy rangi cech X i Y malejąco.

Jeżeli któreś jednostki cechy mają taką samą wartość, to jednostkom tym przypisuje się identyczne rangi, licząc średnią arytmetyczną z rang dla tych samych jednostek.

Przykład 1.
Chcemy obliczyć korelację Spearmana pomiędzy ocenami z testu z matematyki i angielskiego:

Angielski Matematyka
56 66
75 70
45 40
71 60
61 65
64 56
58 59
80 77
76 67
61 63
Niech Angielski będzie cechą X oraz niech Matematyka będzie cechą Y.
Uporządkujmy teraz cechy X i Y malejąco, tj.:
$X \rightarrow 80,76,75,71,64,61,$$61,58,56,45$,
$Y \rightarrow 77,70,67,66,65,63,60,$$59,56,40$.
Tworzymy tabelkę z 2 nowymi kolumnami – rangami dla X i Y:

Cecha X Cecha Y $d_{x}$ $d_{y}$
56 66 9 4
75 70 3 2
45 40 10 10
71 60 4 7
61 65 (6+7)/2=6.5 5
64 56 5 9
58 59 8 8
80 77 1 1
76 67 2 3
61 63 (6+7)/2=6.5 6

gdzie $d_{x}$ i $d_{y}$ to są rangi dla cech X i Y.
Uwaga:
Widzimy, że 2 jednostki mają ocenę 61 (na pozycji 6 i 7), więc:
$ś = \frac{6+7}{2} = \frac{13}{2} = 6,5$.
więc nadamy im rangi 6.5 i 6.5.
Następnie obliczamy różnice i kwadraty różnic dla wyznaczonych rang, tzn.:

Cecha X Cecha Y $d_{x}$ $d_{y}$ $d_{x} – d_{y}$ $(d_{x} – d_{y})^{2}$
56 66 9 4 5 25
75 70 3 2 1 1
45 40 10 10 0 0
71 60 4 7 -3 9
61 65 6.5 5 1.5 2.25
64 56 5 9 -4 16
58 59 8 8 0 0
80 77 1 1 0 0
76 67 2 3 -1 1
61 63 6.5 6 0.5 0.25

Zostało nam to policzenia suma kwadratów różnic rang. Zatem:
$\sum (d_{x} – d_{y})^{2} = 25+1+9+$$2.25+16+0+0+1+$$0.25 = 54.5$
Wobec tego:
$r_{s} = 1 – \frac{6 \cdot 54.5}{10 \ \left(10^{2} – 1\right)} $$= 1 – \frac{327}{990} = 1 – \frac{109}{330} = \frac{221}{330} \approx 0,67$
Odpowiedź: Współczynnik rho wynosi 0,67 co oznacza korelację wysoką.

Intrepretacja współczynnika korelacji rang Spearmana

 

$r_{s}$ interpetacja
poniżej 0,2 korelacja słaba (praktycznie brak związku)
0,2-0,4 korelacja niska (zależność wyraźna)
0,4-0,6 korelacja umiarkowana (zależność istotna)
0,6-0,8 korelacja wysoka (zależność znaczna)
0,8-0,9 korelacja bardzo wysoka (zależność bardzo duża)
0,9-1,0 zależność praktycznie pełna

Korelacja rang Spearmana a korelacja Pearsona

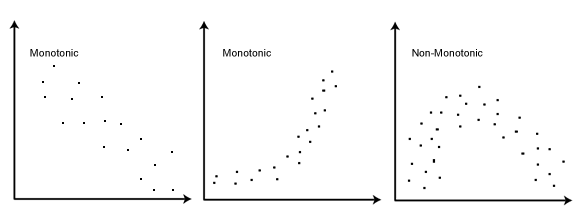
Korelacja rang Spearmana bada związki monotonicze (wykres 1 i 2), w przeciwieństwie do korelacji Pearsona, które bada związki liniowe (jedynie wykres 1)

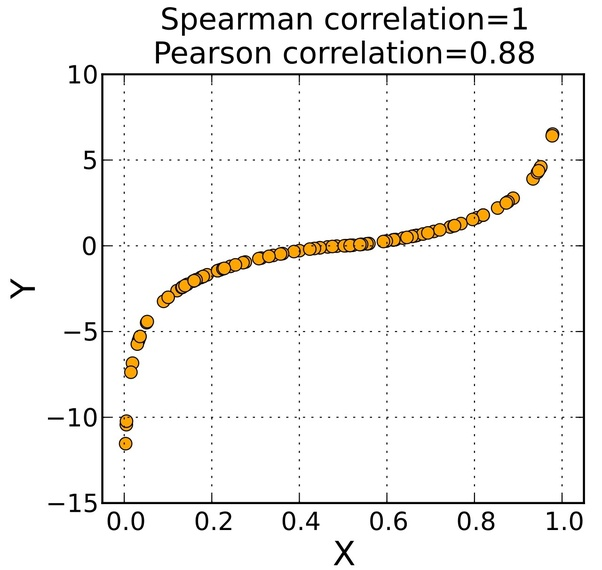
Przykład 2.

Widzimy wykres rozrzutu zmiennej, gdzie relacja nie jest liniowa, tylko „pofalowana”. Współczynnik korelacji Pearsona wyniesie 0.88 a Spearmana 1.

Źrodło: wikipedia.org

Oznacza to, że wartości odstające nie zaburzają korelacji Spearmana tak jak w przypadku korelacji Pearsona.

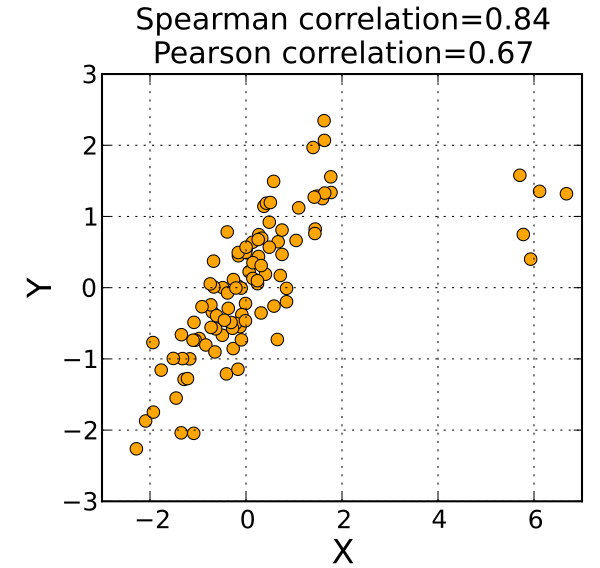
Przykład 3.

Widzimy wykres rozrzutu zmiennej, gdzie mamy po prawej stronie wartości odstające. Współczynnik korelacji Pearsona wyniesie 0.67 a Spearmana 0.843.

Źrodło: wikipedia.org

Istotność korelacji Spearmana

Skąd mamy wiedzieć czy obliczony współczynnik korelacji mamy traktować “na serio”?

Co świadczy “lepiej” o istniejącej korelacji? Współczynnik korelacji równy 0.4 dla 50 par zmiennych czy równy 0.5 dla 5 par zmiennych?

Możemy sprawdzić “wiarygodność” obliczonego współczynnika dla korelacji Spearmana i korelacji Pearsona korzystając  z testu istotności korelacji .
Wtedy możemy z pewnym przyjętym prawdopodobieństwem stwierdzić czy korelacja jest istotna statystycznie.

Typowy przykład

Sędziowie przyznali 10 zawodnikom następujące noty na turnieju tańca solo:

Zawodnik Ocena sędziego 1 Ocena sędziego 2
1 5 7
2 9 8
3 3 6
4 8 7
5 6 8
6 7 5
7 4 10
8 8 6
9 4 5
10 6 8

Oblicz jak silnie skorelowane są oceny sędziów 1 i 2.

Niech X będzie sędzią 1, a Y to sędzia 2.
Uporządkujmy oceny sędziów malejąco, tj.:
$x \rightarrow 9,8,8,7,6,6,5,4,4,3$,
$y \rightarrow 10,8,8,8,7,7,6,6,5,5$.Przydzielamy rangi:

Zawodnik X Y Ranga X Ranga Y
1 5 7 7 5.5
2 9 8 1 3
3 3 6 10 7.5
4 8 7 2.5 5.5
5 6 8 5.5 3
6 7 5 4 9.5
7 4 10 8.5 1
8 8 6 2.5 7.5
9 4 5 8.5 9.5
10 6 8 5.5 3

Rangi X:
Zawodnik 2. dostał notę 9 od sędziego 1, więc dostaje rangę 1.
Zawodnik 3. i 8. dostali oboje 8, więc dostają rangę $\frac{2+3}{2} = 2.5$
Analogicznie przydzielamy rangi Y.

Dalej obliczamy różnice i ich kwadraty:

Zawodnik X Y Ranga X Ranga Y $d$ $d^{2}$
1 5 7 7 5.5 1.5 2.25
2 9 8 1 3 -2 4
3 3 6 10 7.5 2.5 6.25
4 8 7 2.5 5.5 -3 9
5 6 8 5.5 3 2.5 6.25
6 7 5 4 9.5 -5.5 30.25
7 4 10 8.5 1 7.5 56.25
8 8 6 2.5 7.5 -5 25
9 4 5 8.5 9.5 -1 1
10 6 8 5.5 3 2.5 6.25

Wobec tego:
$\sum d_{i}^{2} = 2.25+4+6.25+9+$$6.25+30.25+56.25$$+25+1+6.25=146.5$

Na końcu obliczamy współczynnik rang Supermana:
$r_{s} = 1 – \frac{6 \sum_{i=1}^{n} d_{i}^{2}}{n \ \left(n^{2} – 1\right)} = 1 – \frac{6 \cdot 146.5}{10\left(100-1\right)} =$$ 1 – \frac{879}{990} = \frac{111}{990} = \frac{37}{330} \approx 0,11$

Odpowiedź: Współczynnik rang Spearmana wynosi 0,11 i oznacza ono korelację słabą.

 
Bibliografia:

  • Statystyka ogólna, pod red. Michała Woźniaka, Wyd. 3 poprawione, Kraków, Wydawnictwo Akademii Ekonomicznej w Krakowie, 2002, ISBN 83-7252-113-1
  • Maksimowicz-Ajchel Alicja, Wstęp do statystyki: Metody opisu statystycznego, Warszawa, Wydawnictwo Uniwersytetu Warszawskiego, 2007, ISBN 978-83-235-0267-8
19+
Martyna Szczygieł