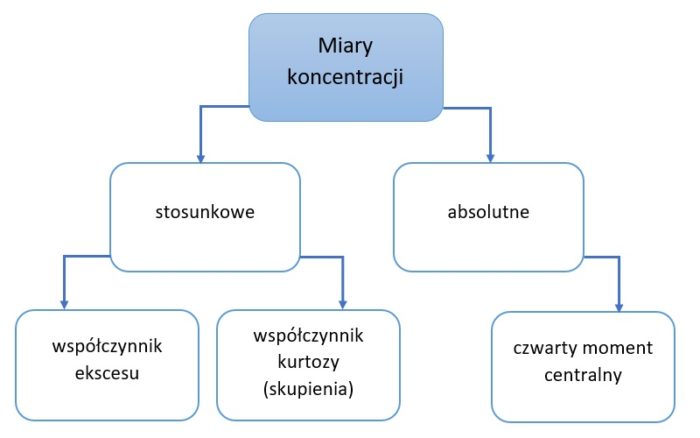
Jak wyglądają rozkłady o różnych koncentracjach?

Miary koncentracji

Czwarty moment centralny
$$\mu_{4}(x)=\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})^{4}}{n_{i}}$$
Współczynnik koncentracji (kurtozy, skupienia) $Ku$ jest stosunkiem czwartego momentu centralnego i odchylenia standardowego podniesionego do potęgi czwartej. To inaczej względny (standaryzowany) czwarty moment centralny:
$$Ku=\frac{\mu_{4}}{s^{4}}$$
Ekces (lub eksces)
$$Ex=Ku-3$$

W niektórych źródłach podawane są wzory:
$$Ku=\frac{\mu_{4}}{s^{4}}-3$$
(kurtoza już ma odjęte 3, nie liczymy ekcesu)

Interpretacja kurtozy

Rozkłady prawdopodobieństwa można podzielić ze względu na wartość kurtozy na rozkłady:

  • $Ku=3$ (i $Ex=0$) – rozkład mezokurtyczny – spłaszczenie rozkładu jest podobne do spłaszczenia rozkładu normalnego (dla którego kurtoza wynosi dokładnie 0).
  • $Ku>3$ (i $Ex>0$) – rozkład leptokurtyczny – wartości cechy bardziej skoncentrowane (bardziej wysmukłe) niż przy rozkładzie normalnym.
  • $Ku<3$ (i $Ex<0$) – rozkład platokurtyczny – kurtoza jest ujemna, wartości cechy mniej skoncentrowane (bardziej spłaszczone) niż przy rozkładzie normalnym.

Przykład:

Liczba wizyt w teatrze $(x_{i})$ Liczba studentów $(n_{i})$
0 16
1 27
2 25
3 21
4 7
5 4

Na innych stronach liczyliśmy, że w tym przykładzie średnia wynosi $\overline{x}=1,88$, a odchylenie standardowe $s=1,321$.

Rozwiązanie:

Liczba wizyt w teatrze $(x_{i})$ Liczba studentów $(n_{i})$ $x_{i}\cdot n_{i}$ $(x_{i}-\overline{x})^{4}\cdot n_{i}$
0 16 0 199,872
1 27 27 16,192
2 25 50 0,005
3 21 63 33,044
4 7 28 141,397
5 4 20 379,034
$\sum$ 100 188 769,544

Czwarty moment centralny jest równy:
$$\mu_{4}(x)=\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})^{4}}{n_{i}}=\frac{769,544}{100}=7,6954$$
Kurtoza jest równa:
$$Ku=\frac{\mu_{4}}{s^{4}}=\frac{7,6954}{1,321^{4}}=2,527$$
Ekces jest równy:
$$Ex=Ku-3=2,527-3=-0,473$$
Interpretacja kurtozy:
W naszym przykładzie $Ku=2,527<3$, a więc mamy rozkład platokurtyczny.

8+
Justyna Chojecka