Trójkąty charakterystyczne to
- trójkąt o kątach $30°$, $60°$, $90°$
- trójkąt o kątach $45°$, $45°$, $90°$
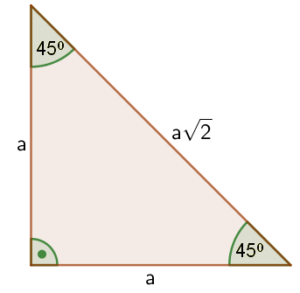
Jest to połowa kwadratu przeciętego wzdłuż przekątnej, czyli powstaje trójkąt równoramienny o długości ramienia $a$ (przyprostokątne mają takie same długości).
Przykład: Oblicz długości pozostałych boków.
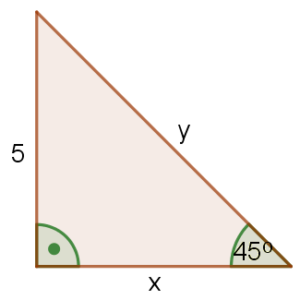


Jedna z przyprostokątnych ma długość $5$, zatem $x = 5$.

Wiemy, że $x=y$.Przeciwprostokątna ma długość
$z \sqrt{2} = 8 \hspace{0,5cm}| :\sqrt{2}$
$x = \frac{8}{\sqrt{2}}$
Usuwamy niewymierność
$x = \frac{8}{\sqrt{2}} \cdot \frac{\sqrt2}{\sqrt2}$$ = \frac{8\sqrt2}{2}$$ = 4 \sqrt2$
Przykład: Jeden z kątów trójkąta prostokątnego ma $45°$ i jeden z jego boków ma długość $10$. Oblicz pole i obwód tego trójkąta.
Musimy rozważyć dwa przypadki.
1° Gdy $10$ jest długością przyprostokątnej, czyli

Stąd pole i obwód:
$P = \frac12 \cdot a \cdot h$$ = \frac 12 \cdot 10 \cdot 10$$ = 50$
$L = a+ h+ b$$ = 10+10+10\sqrt2$$ = 20+10\sqrt2$$ = 10(2+\sqrt2)$
2° Gdy $10$ jest długością przeciwprostokątnej, czyli
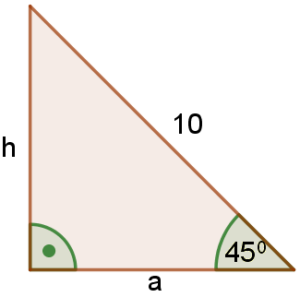
Skoro $10= a \cdot \sqrt2$ to
$a = \frac{10}{\sqrt2}$ (usuwamy niewymierność)
$a = \frac{10}{\sqrt2} \cdot \frac{\sqrt2}{\sqrt2}$$ = \frac{10\sqrt2}{2}$$ = 5\sqrt2$
oraz $a=h$.
Obliczmy pole i obwód trójkąta:
$P = \frac12 \cdot a \cdot h$$ = \frac 12 \cdot 5\sqrt2 \cdot 5\sqrt2 $$ = \frac{25 \cdot \sqrt{2\cdot2}}{2}$$ = \frac{25 \cdot \sqrt4}{2}$$ = \frac{25 \cdot 2}{2}$$ = 25$
$L = a+ h+ b$$ = 5\sqrt2+5\sqrt2+10$$ = 10\sqrt2 + 10$$ = 10(\sqrt2 +1)$
Przykład: Korzystając z danych zamieszczonych na rysunku oblicz pole trójkąta.
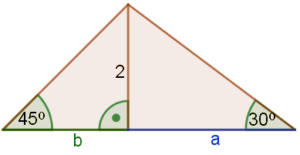
Musimy znaleźć długości odcinków $a$ i $b$, które zsumowane, dają długość podstawy trójkąta.
Z własności trójkąta $45°, 45°, 90°$ długość $b=2$, tak jak wysokość.
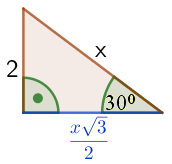
Z własności trójkąta $30°,\, 60°, \, 90°$ długość $2=\frac{x}{2}$, czyli $x=4$.
Stąd $a=\frac{x \sqrt3}{2}$$ = \frac{4 \sqrt3}{2}$$ = 2 \sqrt3$
Długość podstawy trójkąta to $a+b = 2 \sqrt3 +2$, a pole
$P = \frac12 \cdot 2 \cdot 2 \sqrt3 +2$$ = 2 \sqrt3 +2$
Odpowiedź: Pole tego trójkąta wynosi $2 + 2 \sqrt 3$.
