Klasyczna definicja prawdopodobieństwa

Jeżeli $Ω$ jest skończonym zbiorem jednakowo prawdopodobnych zdarzeń elementarnych $ω$
to dla $A\subsetΩ$ liczbę
$$\Large{P(A)=\frac{|A|}{|Ω|}}$$
nazywamy prawdopodobieństwem zdarzenia $A$ gdzie:

  • $|A|$ – moc zbioru $A$ (liczba elementów zbioru $A$)
  • $|Ω|$ – moc zbioru $Ω$ (liczba elementów zbioru $Ω$)

Własności prawdopodobieństwa

  • $0 \leqslant P(A) \leqslant 1$ dla każdego zdarzenia $A\subsetΩ$
  • $P(Ω)=1$, gdzie $Ω$ to zdarzenie pewne
  • $P(\varnothing)=0$, gdzie $\varnothing$ to zdarzenie niemożliwe
  • $P(A) \leqslant P(B)$ gdy $A\subset B\subset Ω$
  • $P(A’)=1-P(A)$, gdzie $A’$ oznacza zdarzenie przeciwne do zdarzenia $A$
  • $P(A\cup B)=P(A)+P(B)-P(A\cap B)$, dla dowolnych zdarzeń $A,B\subsetΩ$
  • $P(A\cup B)\leq P(A)+P(B)$, dla dowolnych zdarzeń $A,B\subsetΩ$
Uwaga: Powyższych własności nie musisz wkuwać! Wybrane wzory matematyczne – CKE strona 17
  • $P(A$\$B)=P(A)-P(A\cap B)$, dla dowolnych zdarzeń $A,B\subsetΩ$

W jakich zadaniach to wykorzystać?

Prawdopodobieństwo – podstawowe definicje

Doświadczenie losowe – działanie które można powtarzać wielokrotnie, posiadające skończoną ilość wyników np. rzut monetą , rzut kostką do gry  .
Zdarzenie elementarne – skutek doświadczenia losowego np. wyrzucenie orła $O$ lub reszki $R$
Zdarzenie losowe $A$ – podzbiór $A$ zbioru zdarzeń elementarnych $Ω$ np. wyrzucenie nieparzystej liczby oczek na kostce do gry $A=${ , , }; jest to zbiór trzyelementowy tzn. $|A|=3$.
A’ – zbiór zdarzeń przeciwnych do zdarzenia losowego $A$.
Ω – zbiór wszystkich zdarzeń elementarnych np. $Ω=\left\{O,R\right\}$, więc $|Ω|=2$; $Ω=${ , , , , , }, więc $Ω=6$.
Zdarzeniem losowym polegającym na wyrzuceniu dwóch orłów może być $A=\left\{O,O\right\}$. Zdarzeniem przeciwnym do tego zdarzenia losowego $A$ nie jest wyrzucenie dwóch reszek! Zdarzeniem przeciwnym jest zdarzenie losowe polegające na nie wyrzuceniu dwóch orłów czyli wyrzucenie $A’=\left\{\left\{O,R\right\},\left\{R,O\right\},\left\{R,R\right\}\right\}$

W jakich zadaniach to wykorzystać?

“Metoda drzewa”

Drzewo stochastyczne jest to graf ilustrujący przebieg wieloetapowego doświadczenia losowego.
Wierzchołkom drzewa są przyporządkowane wyniki poszczególnych etapów doświadczenia.
Krawędziom drzewa są przyporządkowane prawdopodobieństwa uzyskania tych wyników.
Uwaga: Suma prawdopodobieństw przyporządkowanych krawędziom wychodzącym z tego samego wierzchołka jest równa $1$.
Zilustrujemy przykładowe drzewo

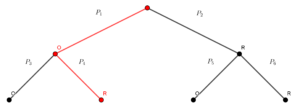
$(1)$ W pierwszym rzucie możemy otrzymać orła lub reszkę.
$(2)$ Orła wyrzucić możemy z prawdopodobieństwem $P_1$, a reszkę z prawdopodobieństwem $P_2$.
$(3)$ Drugi ruch jest zależny od pierwszego, możemy wyrzucić orła lub reszkę.
$(4)$ Możliwe wyniki po drugim ruchu możemy uzyskać z odpowiednimi prawdopodobieństwami $P_3, P_4, P_5, P_6$.
$(5)$ $\color{red}{Gałąź\>drzewa}$ to ciąg krawędzi prowadzących od początku drzewa do jednego z jego ostatnich wierzchołków
Reguła iloczynów – wykorzystujemy ją do obliczenia prawdopodobieństwa zdarzenia opisanego na jednej gałęzi; jest ono równe iloczynowi prawdopodobieństw leżących
na konkretnej gałęzi (np. prawdopodobieństwo zdarzenia oznaczonego kolorem czerwonym $\left\{O,R\right\}$ wynosi $P_1\cdot P_2$)
Reguła sum – wykorzystujemy ją do obliczenia prawdopodobieństwa opisanego przez kilka gałęzi; jest ono równe sumie prawdopodobieństw otrzymanych regułą iloczynów
(np. prawdopodobieństwo zdarzeń $\left\{O,R\right\}$ i $\left\{R,O\right\}$ wynosi $P_1\cdot P_4+P_2\cdot P_5$)

W jakich zadaniach to wykorzystać?

Kombinatoryka

Silnia

Silnią liczby całkowitej dodatniej $n$ nazywamy iloczyn kolejnych liczb całkowitych
od $1$ do $n$ włącznie:

$$\Large{n!=1\cdot 2 \cdot … \cdot n}$$

Ponadto przyjmujemy umowę, że $0!=1$

Symbol Newtona

Dla liczb całkowitych $n$, $k$ spełniających warunki $0\leq k\leq n$ definiujemy współczynnik dwumianowy następująco:

$$\Large{\begin{pmatrix}n\\k\end{pmatrix}=\frac{n!}{k!\cdot (n-k)!}}$$

Wariacje z powtórzeniami

Liczba sposobów, na które z $n$ różnych elementów można utworzyć ciąg, składający się z $k$ niekoniecznie różnych wyrazów, jest równa $$\Large{n^k}$$

Wariacje bez powtórzeń

Liczba sposobów, na które z $n$ różnych elementów można utworzyć ciąg, składający się z $k$ $(1\leq k\leq n)$ różnych wyrazów jest równa

$$\Large{n\cdot (n-1)\cdot …\cdot (n-k+1)=\frac{n!}{(n-k)!}}$$

Permutacje

Liczba sposobów, na które $n$ $(n\geq1)$ różnych elementów można ustawić w ciąg, jest równa $$\Large{n!}$$

Kombinacje

Liczba sposobów, na które spośród $n$ różnych elementów można wybrać $k$ $(0\leq k\leq n)$ elementów, jest równa $$\Large{\begin{pmatrix}n\\k\end{pmatrix}}$$

Uwaga: Tego nie musisz wkuwać! Wybrane wzory matematyczne – CKE strona 16 i 17.
1+
Anita Księżak